Class 7 Maths Chapter 13 Exercise 13.1 – घातांक और घात

Class 7 Maths Chapter 13 Exercise 13.1 – c

NCERT Solutions for Class 7 Maths Chapter 13 Exponents and Powers Ex 13.1 – आज हम आप के लिए Class 7 Maths Chapter 13 लेकर आयें है। जो कि Class 7 Maths Exams के लिए अत्यन्त उपयोगी साबित होगी.  कक्षा 7वीं के विद्यार्थी के लिए यहां पर एनसीईआरटी कक्षा 7 गणित अध्याय 13. (घातांक और घात) प्रश्नावली 13.1 के लिए सलूशन दिया गया है. जोकि एक सरल भाषा में दिया है .ताकि विद्यार्थी को पढने में कोई दिक्कत न आए .इसकी मदद से आप अपनी परीक्षा में अछे अंक प्राप्त कर सकते है.

NCERT Solutions For Class 7th Maths घातांक और घात(प्रश्नावली 13.1)

[su_note note_color=”#ffed23″]1. निम्नलिखित के मान ज्ञात कीजिए :[/su_note]

(i) 2⁶ (ii) 9³ (iii) 11² (iv) 5⁴.
[su_label type=”black”]हल :[/su_label]

(i) 2⁶
= 2 x 2 x 2 x 2 x 2 x 2
= 64 उत्तर

(ii) 9³
= 9 x 9 x 9
= 729 उत्तर

(iii) 11²
= 11 x 11
= 121 उत्तर

(iv) 5⁴
= 5 x 5 x 5 x 5
= 625 उत्तर

[su_note note_color=”#ffed23″]2. निम्नलिखित को घातांकीय रूप में व्यक्त कीजिए :[/su_note]

(i) 6 x 6 x 6 x 6
(ii) t x t
(iii) b x b x b x b
(iv) 5 x 5 x 7 x 7 x 7
(v) 2 x 2 x a x a
(vi) a x a x a x c x c x c x c x d

[su_label type=”black”]हल :[/su_label]

(i) 6 x 6 x 6 x 6 घातांकीय रूप में 6⁴ से व्यक्त किया जा सकता है। इसे 6 की ऊपरी घात 4 या घात 6 की चौथी घात पढ़ा जाता है।
(ii) t x t घातांकीय रूप में t² से व्यक्त किया जा सकता है इसे t की ऊपरी घात 2 या t का वर्ग पढ़ा जाता है।
(iii) b x b x b x b घातांकीय रूप में b⁴ से व्यक्त किया जा सकता है इसे की ऊपरी घात 4 या 6 की घात 4 पढ़ा जाता है।
(iv) 5 x 5 x 7 x 7 x 7 घातांकीय रूप में 5² x 7³ से व्यक्त किया जा सकता है। इसे 5 का वर्ग 7 का घन पढ़ा जाता है।
(v) 2 x 2 x α x α घातांकीय रूप में 2²α² से व्यक्त किया जा सकता है इसे 2 का वर्ग α का वर्ग पढ़ा जाता है।
(vi) α x α x α x c x c x c x c x d घातांकीय रूप में α³c⁴d⁴ से व्यक्त किया जा सकता है। इसे 4 का घन c की चौथी घात d पढ़ा जाता है।

[su_note note_color=”#ffed23″]3. निम्नलिखित संख्याओं में से प्रत्येक को घातांकीय संकेतन में व्यक्त कीजिए:[/su_note]

(i) 512 (ii) 343 (iii) 729 (iv) 3125.
[su_label type=”black”]हल :[/su_label]

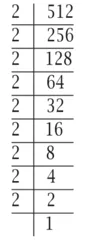
(i) 512 को घातांकी संकेतन में व्यक्त करने के लिए, इसे पहले अभाज्य गुणनखंडन करते हैं।
इस प्रकार, 512 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2
= 2⁹ ; घातांकीय संकेतन के रूप में

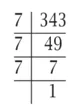
(ii) 343 इसे घातांकीय संकेतन के रूप में व्यक्त करने के लिए पहले हम इसके अभाज्य गुणनखंड करते हैं।
इस प्रकार, 343 =7 x 7 x 7
= 7³; घातांकीय संकेतन के रूप में

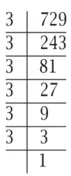
(iii) 729 घातांकीय संकेतन के रूप में व्यक्त करने के लिए पहले हम इसके अभाज्य गुणनखंड करते हैं।
इस प्रकार 729 = 3 x 3 x 3 x 3 x 3 x 3
= 3⁶; घातांकीय संकेतन के रूप में

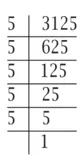
(iv) 3125 इसे घातांकीय संकेतन के रूप में व्यक्त करने के लिए पहले हम इसके अभाज्य गुणनखंड करते हैं।
इस प्रकार 3125 = 5 x 5 x 5 x 5 x 5
= 5⁵: घातांकीय संकेतन के रूप में

[su_note note_color=”#ffed23″]4. निम्नलिखित संख्याओं में से प्रत्येक को घातांकीय संकेतन में व्यक्त कीजिए:[/su_note]

(i) 4³ या 3⁴ (ii) 5³ या 3⁵ (iii) 2⁸ या 8² (iv) 100² या 2¹⁰⁰ (v) 2¹⁰ या 10².

[su_label type=”black”]हल :[/su_label] (i) 4³ = 4 x 4 x 4
= 64
और 3⁴ = 3 x 3 x 3 x 3
= 81
क्योंकि 81 > 64
इसलिए 3⁴, 4³ से बड़ा है।

(ii) 5³ = 5 x 5 x 5
= 125
और 3⁵ = 3 x 3 x 3 x 3 x 3
= 243
क्योंकि 243 > 125
इसलिए 3⁵,5³ से बड़ा है।

(iii) 2⁸ = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2
= 256
और 8² = 8 x 8
= 64
क्योंकि 256 > 64
इसलिए 2⁸, 8² से बड़ा है।

(iv) 100² = 100 x 100
= 10000
और 2¹⁰⁰ = 10240
क्योंकि 10240 > 10000
इसलिए 2¹⁰⁰, 100² से बड़ा है।

(v) 2¹⁰ = (2⁵)²
= (2 x 2 x 2 x 2 x 2)²
= 32 x 32 = 1024
और 10² = 10 x 10
= 100
क्योंकि 1024 > 100
इसलिए 2¹⁰, 10² से बड़ा है।

[su_note note_color=”#ffed23″]5. निम्नलिखित में से प्रत्येक को उनके आभाज्य गणनखंडों की घातों के गुणनफल के रूप में व्यक्त कीजिए :[/su_note]

(i) 648 (ii) 405 (iii) 540 (iv) 3600

[su_label type=”black”]हल :[/su_label] (i) 648 = 2 x 324
= 2 x 2 x 162
= 2 x 2 x 2 x 81
= 2 x 2 x 2 x 3 x 27
= 2 x 2 x 2 x 3 x 3 x 9
= 2 x 2 x 2 x 3 x 3 x 3 x 3
= 2³ x 3⁴

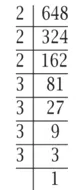
इस प्रकार, 648 = 2³ x 3³ (वांछित अभाज्य गुणनखंडों के घातों के गुणनफल वाला रूप)

(ii) 405 = 3 x 135
= 3 x 3 x 45
= 3 x 3 x 3 x 15
= 3 x 3 x 3 x 3 x 5
= 3⁴ x 5¹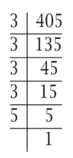

इस प्रकार, 405 = 3⁴ x 5¹
(वांछित अभाज्य गुणनखंडों के घातों के गुणनफल वाला रूप)

(iii) 540 = 2 x 207
= 2 x 2 x 135
= 2 x 2 x 3 x 45
= 2 x 2 x 3 x 3 x 15
= 2 x 2 x 3 x 3 x 3 x 5
= 2² x 3³ x 5¹

इस प्रकार, 540 = 2² x 3³ x 5¹
(वांछित अभाज्य गुणनखंडों के घातों के गुणनफल वाला रूप)

(iv) 3600 = 2 x 1800
= 2 x 2 x 900
= 2 x 2 x 2 x 450
= 2 x 2 x 2 x 2 x 225
= 2 x 2 x 2 x 2 x 3 x 75
= 2 x 2 x 2 x 2 x 3 x 3 x 25
= 2 x 2 x 2 x 2 x 3 x 3 x 5 x 5
= 2² x 3² x 5²

इस प्रकार, 3600 = 2² x 3² x 5²
(वांछित अभाज्य गुणनखंडों के घातों के गुणनफल वाला रूप) घातांक और घात)

[su_note note_color=”#ffed23″]6. सरल कीजिए :[/su_note]

(i) 2 x 10³
(ii) 7² x 2²
(iii) 2³ x 5
(iv) 3 x 4⁴
(v) 0 x 10⁴
(vi) 5² x 3³
(vii) 2⁴ x 3²
(viii) 3² x 10⁴.

[su_label type=”black”]हल :[/su_label] (i) 2 x 10³
= 2 x (10 x 10 x 10)
= 2 x 10 x 10 x 10
= 2000 उत्तर

(ii) 7² x 2²
= 7 x 7 x 2 x 2
= 196 उत्तर

(iii) 2³ x 5
= 2 x 2 x 2 x 5
= 40 उत्तर

(iv) 3 x 4⁴
= 3 x 4 x 4 x 4 x 4
= 768 उत्तर

(v) 0 x 10²
= 0 x 10 x 10
= 0 उत्तर

(vi) 5² x 3³
= 5 x 5 x 3 x 3 x 3
= 675 उत्तर
(vii) 2⁴ x 3²
= 2 x 2 x 2 x 2 x 3 x 3
= 144 उत्तर

(viii) 3² x 10⁴
= 3 x 3 x 10 x 10 x 10 x 10
= 90000. उत्तर

[su_note note_color=”#ffed23″]7. सरल कीजिए :[/su_note]

(i) (-4)³
(ii) (- 3) x (- 2)³
(iii) (-3)² x (- 5)²
(iv) (-2)³ x (- 10)³

[su_label type=”black”]हल :[/su_label] (i) (- 4)³ = (- 4) x (- 4) x (- 4)
= 16 x (- 4) [(- 1) की विषम घात (- 1) और
(- 1) की सम घात (+ 1) है]
= – 64 उत्तर

(ii) (- 3) x (- 2)³ = (- 3) x (- 2) x (- 2) x (- 2)
= 6 x 4 [∵ (- 1) की सम घात (+ 1) है]
= 24 उत्तर

(iii) (- 3)² x (- 5)² = (- 3) – (- 3) x (- 5) x (- 5)
= 9 x 25 [∵ (- 1) की सम घात (+ 1) है]
= 225 उत्तर ”

(iv) (- 2)³ x (- 10)³ = [(- 2) x (- 2) x (- 2)] x [(- 10) x (- 10) x (- 10)]
= (- 8) x (- 1000)
[∵ (- 1) की विषम घात (- 1) है]
= 8000 उत्तर
[∵ (- 1) की सम घात (+ 1) है]

[su_note note_color=”#ffed23″]8. निम्नलिखित संख्याओं की तुलना कीजिए :[/su_note]

(i) 2.7 x 10¹² ; 1.5 x 10⁸ (ii) 4 x 10¹⁴ ; 3 x 10¹⁷.

[su_label type=”black”]हल :[/su_label] (i) 2.7 x 10¹²
= 2.7 x 10 x 10 x 10 x 10 x 10 x 10⁷

= 270000 x 10⁷
1.5 x 10⁸
= 1.5 x 10¹ x 10⁷

= 15 – 10⁷
क्योंकि 270000 > 15
⇒ 270000 x 10⁷ > 15 x 10⁷
इसलिए 2.7 x 10¹², 1.5 x 10⁸ से बड़ी है। उत्तर

(ii) 4 x 10¹⁴
.     3 x 10¹⁷
= 3 x 10 x 10 x 10 x 10¹⁴
= 3000 x 10¹⁴
क्योंकि 3000 > 4
⇒ 3000 x 10¹⁴ > 4 x 10¹⁴
इसलिए 3 x 10^17, 4 x 10¹⁴ से बड़ी है। उत्तर

इस पोस्ट में आपको class 7 maths chapter 13 exponents and powers pdf class 7 maths chapter 13 pdf solutions NCERT Solutions for Class 7 Maths Exercise 13.1 Chapter 13 Exponents and Powers ,Class 7 maths chapter 13 worksheet class 7 maths exercise 13.1 solutions class 7 maths chapter 13 exercise 13.1 question Class 7 Maths Chapter 13 Exponents and Powers Ex 13.1 एनसीईआरटी समाधान कक्षा 7 गणित अध्याय 13 अभ्यास 13.1 कक्षा 7 गणित अध्याय 13 अभ्यास 13.1 – घातांक और घात से संबंधित पूरी जानकारी दी गई है अगर इसके बारे में आपका कोई भी सवाल या सुझाव हो तो नीचे कमेंट करके हम से जरूर पूछें और अगर आपको यह जानकारी फायदेमंद लगे तो अपने दोस्तों के साथ शेयर जरूर करें.

NCERT Solutions for Class 7 Maths Chapter 13 घातांक और घात Exercise 13.1
NCERT Solutions for Class 7 Maths Chapter 13 घातांक और घात Exercise 13.2
NCERT Solutions for Class 7 Maths Chapter 13 घातांक और घात Exercise 13.3