NCERT Solutions for Class 10 Maths Chapter 2 – बहुपद

Class 10th Maths बहुपद (प्रश्नावली 2.4)

(i) 2????² + ????² – 5???? + 2; 7,1,- 2
(ii) ????³ – 4????² + 5???? – 2; 2, 1,1
हल : (i) मान लीजिए p(????) = 2????² + ????² – 5???? + 2
इसकी तुलना α????³ + b????² + cx + d से करने पर
∴ α = 2, b = 1, c = – 5, d = 2
अब,

∴ का एक शून्यक है।
और p(1) = 2(1)³ + (1)² – 5 (1) + 2
= 2 + 1 – 5 + 2 = 5 – 5 = 0
∴ 1, p(????) का एक शून्यक है।
साथ ही, p(-2) = 2(-2)³ + (-2)² -5 (-2) + 2
= – 16 + 4 + 10 + 2
= – 16 + 16 = 0
∴ – 2, p(????) का एक शून्यक हैं।
उपरोक्त चर्चा से, यह स्पष्ट है कि दिए गए बहुपद के शून्यक हैं। मान लीजिए यह शून्यक हैं :

अब,







उपरोक्त चर्चा से यह स्पष्ट है कि शून्यकों और गुणांकों में संबंध है।
(ii) मान लीजिए p(????) = ????3 – 4????2 + 5???? – 2 इसकी तुलना α????³ + b????² + c???? + d से करने पर
∴ α = 1, b = – 4, c = 5, d = – 2
अब p(2) = (2)³ – 4(2)² + 5(2) – 2
= 8 – 16 + 10 – 2 = 18 – 18 = 0
∴ 2, p (2) का एक शून्यक है।
और p(1) = (1)³ – 4(1)² + 5(1) – 2
= 1 – 4 + 5-2 = 6 – 6 = 0
उपरोक्त चर्चा से, यह स्पष्ट है कि 2, 1, 1 दिए गए बहुपद के शून्यक हैं। मान लीजिए यह शून्यक हैं :
α = 2, β = 1, ???? = 1
अब, α+β+???? = 2 + 1 + 1 = 4

αβ+β????+????α = (2)(1) + (1)(1) + (1)(2)
= 2 + 1 + 2 = 5

αβ???? = (2) (1) (1) = 2

उपरोक्त चर्चा से यह स्पष्ट है कि शून्यकों और गुणांकों में संबंध है।

हल : त्रिघात बहुपद का सर्वव्यापक व्यंजक है :
α????² + b????² + c???? + d
मान लीजिए α, β, y इसके शून्यक हैं।
∴ α, β, y = शून्यकों का योग = 2
αβ + βy + yα
= शून्यकों के गुणनफलों का योग
= – 7
αβy = शून्यकों का गुणनफल = – 14
∴ α????³ + b????² + c???? + d = k[(???? – α) (???? – β) (???? – y)] जहाँ k कोई एक अचर है।
= k[????³ – (α + β + y)????² + (αβ + By + yo) ???? – αβy] = k[????³ – 2????² – 7???? + 14] [(1) का प्रयोग करने पर] k, के भिन्न-भिन्न मानों के लिए, हम भिन्न-भिन्न त्रिघात बहुपद प्राप्त करते हैं।

प्रश्न 3. यदि बहुपद x³ – 3x² + x + 1 के शून्यक a – b, a, a + b, हो, तो a और b ज्ञात कीजिए।
हल : मान लीजिए ⊘p(????) = ????³ – 3????² + ???? + 1
और इसके शून्यक α – b, α, α + b हैं।
α – b, p(????) का एक शून्यक है।
∴ p(α – b) = 0
या (α – b)³ – 3(α – b)² + (α – b) + 1 = 0
या [α³ – b³ – 3α²b + 3αb³] – 3[α² + b² – 2αb] + α – b + 1 = 0
या α³ – b³ – 3α²b + 3αb² – 3α² – 3b² + 6αb + α – b + 1 = 0 …(1)
और α, p (????) का शून्यक है …(दिया है)
∴ p(α) = 0
या α³ – 3α³ + α + 1 = 0
साथ ही, α + b, p(????) का शून्यक है …(दिया है)
∴ p(α + b) = 0
या (α + b)³ – 3(α + b)² + (α + b) + 1 = 0
या (α³ + b³ + 3α²b + 3αb²) – 3 (α² + b² + 2αb) + α + b – 1 = 0
या α³ + b³ + 3α²b + 3αb² – 3α² – 3b² – 6αb + α + b + 1 = 0 …(3)
(1) और (3), को जोड़ने पर हम प्राप्त करते हैं।
2α³ + 6αb² – 6α² – 6b² + 2α + 2 = 0
या α + 3αb² – 3α² – 3b² + α + 1 = 0
या (α³ – 3α³ + α + 1) + (3αb² – 3b²) = 0
या 0 + 3b² (α – 1) = 0 [(2) का प्रयोग करने से] α – 1 = 0
α = 1
(3) और (4), से हम प्राप्त करते हैं।
(1)³ + b³ + 3(1)²b + 3(1)b² – 3(1)² – 3b² – 6(1)b + 1 + b + 1 = 0
या 1 + b³ + 3b + 3b²-3 – 3b² – 6b + b + 2 = 0
या b³ – 2b = 0 या b (b² – 2) = 0
या b² – 2 = 0 या b² = 2 या
या b = ±√2
अतः α = 1, b = ±√2
वैकल्पिक हल
दिया है कि बहुपद ????³ – 3????² + ???? + 1 के तीन शून्यक क्रमश: α – b, α, α + b हैं।
अब, शून्यकों का योगफल = (α – b) + α + (α + b)
= α – b + α + α + b
= 3α
परंतु गुणांकों का प्रयोग करके शून्यकों का योगफल
= -????² का गुणांक/????³ का गुणांक

∴ 3α = 3 या α = 1
साथ ही, शून्यकों का गुणनफल = (α – b). α (α + b)
= (α² – b²) α
α का मान भरने पर हम प्राप्त करते हैं
= (1² – b²). 1
= (1 – b²)
परंतु गुणांकों का प्रयोग करके शून्यकों का गुणनफल
= – अचर पद/????³ का गुणांक

∴ 1 – b² = – 1
– b² = – 1 – 1
– b² = – 2 या b² = 2
b = ±√2
अतः α = 1 और b = ±√2

हल : दिया है कि दो शून्यक (2 + √3) और (2 – √3) हैं।
∴ [????-(2+√3)][????-(2-√3)] दी गई बहुपद के गुणनखंड हैं।
अब, [???? – (2 + √3)] [???? – (2-√3)] = ????² – [2 – √3 + 2 + √3]???? + [(2 + √3) (2 – √3)] = ????² – 4???? + [(2)² – (√3)²] = ????² – 4???? + 1
∴ (????² – 4???? + 1) दी गई बहुपद का गुणनखंड है। अब दी गई बहुपद और (????² – 4???? + 1) पर विभाजन एल्गोरिथ्म का उपयोग करने पर

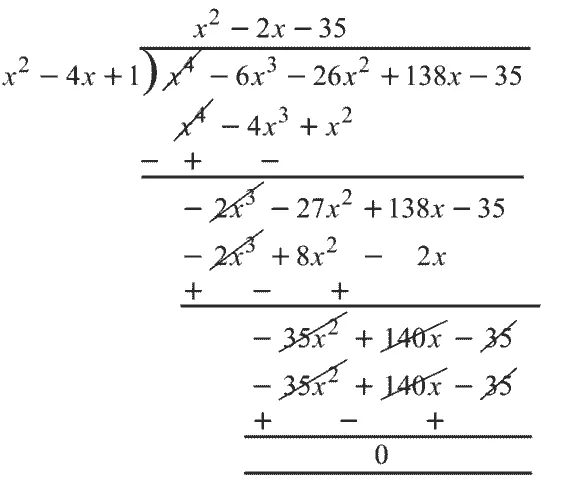
∴ ????⁴ – 6????³ – 26????² + 138???? – 35
= (????² – 4???? + 1) (????² – 2???? – 35) |S = – 2
= (????² – 4???? + 1) [????² + 5???? – 7???? – 35) |P = – 35
= (????² – 4???? + 1) [???? (???? + 5)- 7 (???? + 5)] = (????² – 4???? + 1) (???? + 5) (???? – 7)
अब, बहुपद के अन्य शून्यक हैं।
???? + 5 = 0 या ???? – 7 = 0
???? = – 5 या ???? = 7
∴ दी गई चार घात वाली बहुपद के शून्यक हैं :
2 + √3, 2 – √3, – 5,7

हल : दिया है कि बहुपद ????⁴ – 6????³ + 16????² – 25???? + 10 को एक अन्य बहुपद ????² – 2???? + k से भाग दिया जाता है, तो शेषफल ???? + α आता है। इसलिए सर्वप्रथम हम
????⁴ – 6????³ + 16????² – 25???? + 10 को ????² – 2???? + k, से भाग करते हैं और भागफल और शेषफल ज्ञात करते हैं :

∴ बहुपद ????⁴ – 6????³ + 16????² – 25???? + 10
के लिए विभाजन एल्गोरिथ्म से
= (????² – 2???? + k) [????² – 4???? + (8 – k)] + [(-9 + 2k) ???? + (10 – 8k + k²] ∴ भागफल = ????² – 4???? + (8 – k)
और शेषफल = (-9 + 2k)???? + (10 – 8k + k²)
परंतु शेषफल = ????² + α …(दिया है)
∴ (-9 + 2k)???? + (10 – 8k + k²)
= ???? + α
समान गुणांकों की तुलना करने से
– 9 + 2k = 1 या 10 – 8k + K² = α
2k = 1 + 9
2k = 10, हम प्राप्त करते हैं

अब, 10 – 8k + k² = α

k का मान प्रतिस्थापित करने पर हम प्राप्त करते हैं:
10 – 8 x 5 + (5)² = α
10 – 40 + 25 = α
k = 5
– 5 = α
α = – 5
अत: k = 5 और α = – 5

इस पोस्ट में आपको NCERT Solutions Class 10 Maths Chapter 2 – बहुपद Class 10 Maths Chapter 2 Solutions Exercise 2.2 Class 10 Maths in Hindi Exercise 2.3 Class 10 Maths NCERT Solutions in Hindi Class 10 Math Chapter 2 Polynomials NCERT Solutions for Class 10 Maths Chapter 2 Polynomial NCERT Class-10 प्रश्नावली 2.1 Mathematics 2. बहुपद एनसीईआरटी समाधान कक्षा 10 गणित अध्याय 2 बहुपद से संबंधित पूरी जानकारी दी गई है अगर इसके बारे में आपका कोई भी सवाल या सुझाव हो तो नीचे कमेंट करके हम से जरूर पूछें और अगर आपको यह जानकारी फायदेमंद लगे तो अपने दोस्तों के साथ शेयर जरूर करें.