NCERT Solutions for Class 10 Maths Chapter 2

Class 10 Maths Chapter 2 – बहुपद | NCERT Solutions for Class 10 Maths Chapter 2 Polynomials | Class 10 Maths Chapter 2 Polynomial (Hindi Medium)

NCERT Solutions Class 10 Maths Chapter 2 बहुपद– जो विद्यार्थी 10 कक्षा में पढ़ रहे है एनसीईआरटी समाधान कक्षा 10 गणित अध्याय 2 यहाँ से प्राप्त करें .कक्षा 10 के छात्रों के लिए यहाँ पर गणित विषय के अध्याय 2 का पूरा समाधान दिया गया है। जो भी गणित विषय में अच्छे अंक प्राप्त करना चाहते है उन्हें यहाँ पर एनसीईआरटी समाधान कक्षा 10 गणित अध्याय 2. (बहुपद) का पूरा हल मिल जायेगा। जिससे की छात्रों को तैयारी करने में किसी भी मुश्किल का सामना न करना पड़े। इस NCERT Solutions For Class 10th Maths Chapter 2 Polynomial की मदद से विद्यार्थी अपनी परीक्षा की तैयारी अच्छे कर सकता है और परीक्षा में अच्छे अंक प्राप्त कर सकता है.

Class	Class 10
Subject	Maths
Chapter	Chapter 2
Chapter Name	बहुपद

NCERT Solutions For Class 10 गणित Chapter 1 बहुपद

मान लीजिए α, β, ???? किसी त्रिघात बहुपद के शून्यक हों, तो बहुपद है : p (x) = k{x³ – (α + β + ????)????² + (αβ + βy + yα)???? – αβy} जहाँ k कोई अचर है।

Class 10th Maths बहुपद (प्रश्नावली 2.1)

प्रश्न 1. किसी बहुपद p (x) के लिए, y = p (x) का ग्राफ नीचे आकृति में दिया है, प्रत्येक स्थिति में, p (x) के शून्यकों की संख्या ज्ञात कीजिए।

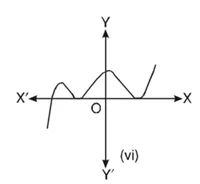
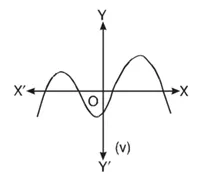
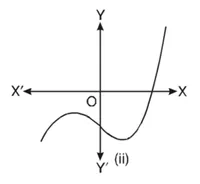
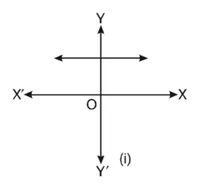
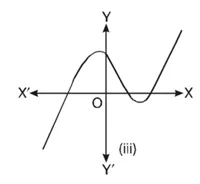
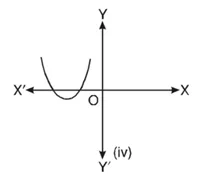
हल : किसी बहुपद p(????) के लिए, 1 = p(????) को ग्राफ नीचे आकृति में दिया है।
प्रत्येक स्थिति में, p(????) के शून्यकों की संख्या नीचे दी गई है :
(i) ग्राफ से यह स्पष्ट है कि यह x-अक्ष को किसी भी बिंदु पर नहीं मिलता। अतः इसका कोई भी शून्यक नहीं है।
(ii) ग्राफ से यह स्पष्ट है कि यह x-अक्ष को केवल एक बिंदु पर मिलता है। अतः इसका कोई भी शून्यक नहीं है।
(iii) ग्राफ से यह स्पष्ट है कि x-अक्ष को तीन बिंदुओं पर मिलता है।
(iv) ग्राफ से यह स्पष्ट है कि यह x-अक्ष को दो बिंदुओं पर मिलता है। अतः इसके शून्यकों की संख्या दो है।
(v) ग्राफ से यह स्पष्ट है कि यह x-अक्ष को चार बिंदुओं पर मिलता है। अतः इसके शून्यकों की संख्या चार है।
(vi) ग्राफ से यह स्पष्ट है कि यह x-अक्ष को तीन बिंदुओं पर मिलता है। अत: इसके शून्यकों की संख्या तीन है।

Class 10th Maths बहुपद (प्रश्नावली 2.2)

प्रश्न 1. निम्न द्विघात बहुपदों के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के संबंध की सत्यता की जाँच कीजिए :
(i) ????² – 2???? – 8
(ii) 4s² – 4s +1
(iii) 6????² – 3 – 7????
(iv) 4u²– + 8u (v) t² – 15
(vi) 3????² – ???? – 4

हल : (i) दी गई द्विघात बहुपद है
????² – 2???? – 8
S = – 2
P = – 8
= ????² – 4???? + 2???? – 8
= ???? (???? – 4) + 2 (???? – 4)
= (???? – 4) (???? + 2)
????² – 2???? – 8 का मान शून्य है
यदि (???? – 4) = 0 या (???? + 2) = 0
यदि ???? = 4 या ???? = – 2
????² – 2???? – 8 के शून्यक – 2 और 4 हैं।
अब, शून्यकों का योग = (-2) + (4) = 2

= – x का गुणांक/????² का गुणांक
शून्यकों का गुणनफल = (-2) (4) = – 8
= अचर पद/????² का गुणांक
अतः शून्यकों तथा गुणांकों के बीच के संबंध का सत्यापन किया जाता है।
(ii) दी गई द्विघात बहुपद हैं
4s² – 4s +1
= 4s² – 2s – 2s + 1 S = – 4
= 2s (2s-1)-1 (2s – 1) P = 4 x 1 = 4
= (2s – 1) (2s – 1)
4s² – 4s + 1 का मान शून्य है।
यदि (2s – 1) = 0 या (2s – 1) = 0
यदि या
अत: 4s² – 4s + 1 के शून्यक और हैं।
अब शून्यकों का योग
= -s का गुणांक/s² का गुणांक
शून्यकों का गुणनफल
= अचर पद/s² का गुणांक
अतः, शून्यकों तथा गुणांकों के बीच के संबंध का सत्यापन किया जाता है।
(iii) दी गई द्विघात बहुपद है :6????² – 3 – 7????
= 6????² – 7???? – 3 S = – 7
= 6????² – 9???? + 2???? – 3 P = 6x – 3 = – 18
= 3???? (2???? – 3) + 1 (2???? – 3)
= (2???? – 3) (3???? + 1)
6????² – 3 – 7???? का मान शून्य है
यदि (2???? – 3) = 0 या 3???? + 1 = 0
यदि या
अत: 6????² – 3 – 7???? के शून्यक और हैं।

अब, शून्यकों का योग

= x का गुणांक/????² का गुणांक
शून्यकों का गुणनफल
अचर का पद/????² का गुणांक
अतः, शून्यकों तथा गुणांकों के बीच के संबंध को सत्यापित किया जाता है।
(iv) दी गई द्विघात बहुपद हैं :4u² + 8u = 4u (u + 2)
4u² + 8u का मान शून्य है
यदि 4u = 0 या u + 2 = 0
यदि u = 0 या u = – 2
अत:, 4u² + 8u के शून्यक 0 और – 2 हैं।
अब, शून्यकों का योग = 0 + (-2)

= u का गुणांक/u² का गुणांक
शून्यकों का गुणनफल = (0) (-2) = 0
= अचर का पद/u² का गुणांक
अतः, शून्यकों तथा गुणांकों के बीच के संबंध को सत्यापित किया जाता है।
(v) दी गई द्विघात बहुपद हैं,t² – 15
= t² – (√15)²
= (t – √15) (t + √15)
t² – 15 का मान शून्य है।
यदि t – √15 = 0 या t + √15 = 0
यदि t = √15 या t = – √15
अतः t² – 15 के शून्यक – √15 और √15 है।
अब, शून्यकों का योग = -√15 + √15

= – 1 का गुणांक/t² का गुणांक
शून्यकों का गुणनफल = (-√15)(√v15)

= अचर का पद / t² का गुणांक
अत:, शुन्यकों तथा गुणांकों के बीच के संबंध को सत्यापित किया जाता है।
(vi) दी गई द्विघात बहुपद हैं :3????² – ???? – 4
= 3????² + 3???? – 4???? – 4 S = – 1
= 3???? (???? + 1) – 4(???? + 1) P = 3x – 4 = – 12
= (???? + 1) (3???? – 4)
3????² – ???? – 4 का मान शून्य है
यदि (???? + 1) = 0 या 3???? – 4 = 0
यदि ???? = – 1 या
अत 3????² – ???? – 4 के शून्यक – 1 और में है।
अब, शून्यकों का योग

= – ???? का गुणांक/????² का गुणांक
शून्यकों का गुणनफल
= अचर का पद/????² का गुणांक
अतः, शून्यकों तथा गुणांकों के बीच के संबंध को सत्यापित किया जाता है।

प्रश्न 2. एक द्विघात बहुपद ज्ञात कीजिए, जिसके शून्यकों के योग तथा गुणनफल क्रमशः दी गई संख्याएं हैं :

(i) (ii) (iii) 0,√5 (vi) 1,1 (iv) (v) 4,1

हल :

(i) दिया गया है कि शून्यकों का योग तथा शून्यकों का गुणनफल क्रमशः

और – 1 है।
मान लीजिए कि α????² + b???? + c एक द्विघात समीकरण है तथा α और β इसके
शून्यक हैं।
∴ α + β = शून्यकों का योग =
और αβ = शून्यकों का गुणनफल = – 1
अब, α????² + b???? + c
= k (???? – α) (???? – β)
जहाँ k कोई अचर है।
= k [????² – (α + β) x + αβ]

k के भिन्न-भिन्न मानों के लिए, हम भिन्न-भिन्न द्विघात बहुपद प्राप्त करते हैं।
(ii) दिया गया है कि शून्यकों का योग तथा शून्यकों का गुणनफल क्रमशः √2 और है।
मान लीजिए कि α????² + b???? + c एक द्विघात समीकरण है तथा α और β इसके शून्यक हैं।
∴ α + β = शून्यकों का योग = √2
और αβ = शून्यकों का गुणनफल =
अब, α????² + b???? + c = k (???? – α) (???? – β)
जहाँ k कोई अचर है।
k[????² -(α + β)???? + αβ]
k के भिन्न-भिन्न मानों के लिए, हम भिन्न-भिन्न द्विघात बहुपद प्राप्त करते हैं।
(iii) दिया गया है कि शून्यकों का योग तथा शून्यकों का गुणनफल क्रमशः 0 और √5 है।
मान लीजिए कि α????² + b???? + c एक द्विघात समीकरण है तथा α और β इसके शून्यक हैं।
∴ α + β = शून्यकों का योग = 0
और αβ = शून्यकों का गुणनफल = √5
अब, α????² + b???? + c = k(???? – α) (???? – β)
जहाँ k कोई अचर है।
= k[????² – (α + β) ???? + αβ] = k[????² – 0???? + √5] = k[????² + √5] k के भिन्न-भिन्न मानों के लिए, हम भिन्न-भिन्न द्विघात बहुपद प्राप्त करते हैं।
(iv) दिया गया है कि शून्यकों का योग तथा शून्यकों का गुणनफल क्रमश: 1 और 1 है। मान लीजिए कि α????² + b???? + c एक द्विघात समीकरण है तथा α और β इसके शून्यक हैं।
∴ α + β = शून्यकों का योग = 1
और αβ = शून्यकों का गुणनफल = 1
अब, α????² + b???? + c = k (???? – α) (???? – β)
जहाँ k कोई अचर है।
= k [????² – (α + β)???? + αβ] = k [????² – 1???? + 1] = k [????² – ???? + 1] k के भिन्न-भिन्न मानों के लिए, हम भिन्न-भिन्न द्विघात बहुपद प्राप्त करते हैं।
(v) दिया गया है कि दी हुई बहुपद शून्यकों का योग तथा शून्यकों का गुणनफल क्रमशः और में है।
मान लीजिए कि α????² + b???? + c एक द्विघात बहुपद है तथा α और β इसके शून्यक हैं।
क्रमशः
∴ α + β = शून्यकों का योग =
और αβ शून्यकों का गुणनफल =
अब, α????² + b???? + c = k (???? – α) (???? – β)
जहाँ k कोई अचर है।
= k [????² – (α + β)???? + αβ]

k के भिन्न-भिन्न मानों के लिए, हम भिन्न-भिन्न द्विघात बहुपद प्राप्त करते हैं।
(vi) दिया गया है कि दी गई बहुपद के शून्यकों का योग और शून्यकों का गुणनफल क्रमशः 4, 1 है।
मान लीजिए कि α????² + b???? + c एक द्विघात बहुपद है तथा α और β इसके शून्यक हैं।
∴ α + β = शून्यकों का योग = 4
और αβ = शून्यकों का गुणनफल = 1
अब, α????² + b???? + c = k (???? – α) (???? – β)
जहाँ k कोई अचर है।
= k [????² – (α + β) ???? + αβ)
= k [????² – 4???? + 1] k के भिन्न-भिन्न मानों के लिए, हम भिन्न-भिन्न द्विघात बहुपद प्राप्त करते हैं।