Class 10 Maths Chapter 13 Exercise 13.1 – पृष्ठीय क्षेत्रफल और आयतन

NCERT Solutions for Class 10 Maths Chapter 13 Surface Areas And Volumes Ex 13.1 – जो विद्यार्थी 10वीं कक्षा में पढ़ रहे है उनके लिए यहां पर एनसीईआरटी कक्षा 10 गणित अध्याय 13. (पृष्ठीय क्षेत्रफल और आयतन) प्रश्नावली 13.1 के लिए सलूशन दिया गया है. जोकि एक सरल भाषा में दिया है .ताकि विद्यार्थी को पढने में कोई दिक्कत न आए .इसकी मदद से आप अपनी परीक्षा में अछे अंक प्राप्त कर सकते है. इसलिए निचे आपको एनसीईआरटी समाधान कक्षा 10 गणित अध्याय 13 पृष्ठीय क्षेत्रफल और आयतन प्रश्नावली 13.1 दिया गया है .

NCERT Solutions For Class 10th Maths पृष्ठीय क्षेत्रफल और आयतन (प्रश्नावली 13.1)

जब तक अन्यथा न कहा जाए, लीजिए।

1. दो घनों, जिनमें से प्रत्येक का आयतन 64 cm² है, के संलग्न फलकों को मिलाकर एक ठोस बनाया जाता है। इससे प्राप्त घनाभ का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

हल : मान लीजिए घन की प्रत्येक भुजा = x cm
घन का आयतन = 64 cm²

[घन का आयतन = (भुजा)²

X² = 64

X = 4 cm

घन की भुजा = 4 cm.
जब घनों को साथ-साथ जोड़ा जाता है तो घनाभ बन जाता है।
जिसकी लंबाई = 2x cm = 2(4) cm = 8 cm
चौड़ाई = x cm = 4 cm
ऊँचाई = x cm = 4 cm

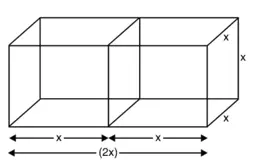
घनाभ का पृष्ठीय क्षेत्रफल

= 2 [Lb + bh + h] = 2 [8 x 4 + 4 x 4 + 4 x]8 cm²
= 2 [ 32 + 16 + 3]2 cm²
= 2 [8]0 cm²
∴ घनाभ का पृष्ठीय क्षेत्रफल = 160 cm² उत्तर

2. कोई बर्तन एक खोखले अर्धगोले के आकार का है जिसके ऊपर एक खोखला बेलन अध्यारोपित है। अर्धगोले का व्यास 14 cm है और इस बर्तन (पात्र) की कुल ऊँचाई 13 cm है। इस बर्तन का आंतरिक पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

हल : अर्धगोले का व्यास = बेलन का व्यास
= 14 cm
2R = 14 cm

अर्धगोले की त्रिज्या (R) = 7 cm

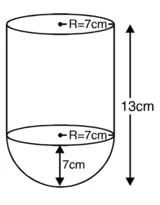
बर्तन की कुल ऊँचाई = 13 cm
∴ बेलन की ऊँचाई = (13 – 7) cm = 6 cm

बर्तन का आंतरिक पृष्ठीय क्षेत्रफल

= बेलन का आंतरिक पृष्ठीय क्षेत्रफल + अर्धगोले का आंतरिक पृष्ठीय क्षेत्रफल

= 2????RH + 2????R²

= 2????R [H + R]

= 44 x 13 cm²

= 572 cm²

बर्तन का आंतरिक पृष्ठीय क्षेत्रफल

= 572 cm²

3. एक खिलौना त्रिज्या 3.5 cm वाले एक शंकु के आकार का है, जो उसी त्रिज्या वाले एक अर्धगोले पर अध्यारोपित है। इस खिलौने की संपूर्ण ऊँचाई 15.5 cm है। इस खिलौने का संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

हल :

शंकु की त्रिज्या = अर्धगोले की त्रिज्या (R) = 3.5 cm

खिलौने की कुल ऊँचाई = 15.5 cm

∴ शंकु की ऊँचाई (H) = (15.5 – 3.5) cm = 12 cm

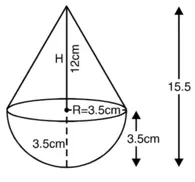
शंकु की तिर्यक ऊँचाई

= √12.25+144

= (3.5) + (12)2 cm = 12.25 +144 cm

= 156.25 cm

शंकु की तिर्यक ऊँचाई (I) = 12.5 cm

बर्तन का कुल पृष्ठीय क्षेत्रफल = शंकु का पृष्ठीय क्षेत्रफल + अर्धगोले का पृष्ठीय क्षेत्रफल

= ????Rl + 2????R²
= ????R [l + 2R]

∴ बर्तन का कुल पृष्ठीय क्षेत्रफल

= 214.5 cm² उत्तर

4. भुजा 7 cm वाले एक घनाकार ब्लॉक के ऊपर एक अर्धगोला रखा हुआ है। अर्धगोले का अधिकतम व्यास क्या हो सकता है ? इस प्रकार बने ठोस का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

हल : घनाकार ब्लॉक की भुजा = 7 cm

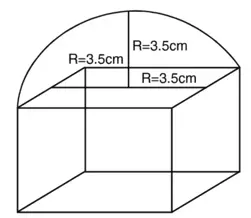
अर्धगोले का अधिकतम व्यास = घनाकार ब्लॉक की भुजा = 7 cm

2R = 7 cm

ठोस का पृष्ठीय क्षेत्रफल = (घन का पृष्ठीय क्षेत्रफल) – (अर्ध गोले के आधार का क्षेत्रफल) + (अर्ध गोले का वक्र पृष्ठीय क्षेत्रफल)

= 6l² – ????R² + 2????R²

= 6l² + ????R²

= 332.5 cm² उत्तर

5. एक घनाकार ब्लॉक के एक फलक को अंदर की ओर से काट कर एक अर्धगोलाकार गड्ढा इस प्रकार बनाया गया है कि अर्धगोले का व्यास घन के एक किनारे के बराबर है। शेष बचे ठोस का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

हल : मान लीजिए घन की भुजा = α

∴ अर्धगोले का व्यास = घन की भुजा

2R = α

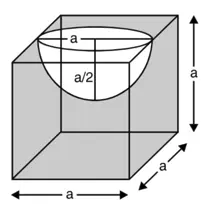
शेष बचे ठोस का पृष्ठीय क्षेत्रफल

= घनाभ का कुल पृष्ठीय क्षेत्रफल – घन के तल का क्षेत्रफल + अर्धगोले का आंतरिक वक्र पृष्ठीय क्षेत्रफल

= 6 (भुजा)² – ????R² + 27R^????

= 6(α)² + ????R²

वर्ग इकाईयां उत्तर

6. दवा का एक कैप्सूल (capsule) एक बेलन के आकार का है जिसके दोनों सिरों पर एक-एक अर्धगोला लगा हुआ है (देखिए आकृति)। पूरे कैप्सूल की लंबाई 14 mm है और उसका व्यास 5 mm है। इसका पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

हल : कैप्सूल का व्यास = अर्धगोले का व्यास = बेलन का व्यास = 5 mm
∴ 2R = 5 mm

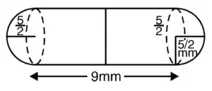
कैप्सूल की आंतरिक लंबाई = 14 mm

बेलनाकार भाग की ऊँचाई
= (14 – 5) mm
H = 9 mm

कैप्सूल का पृष्ठीय क्षेत्रफल = बेलन का पृष्ठीय क्षेत्रफल + 2 अर्धगोले का पृष्ठीय क्षेत्रफल

= 2????RH + 2(2????R²)

= 2????RH + 4????R²

= ????R [H + 2]R

= 22 x 5 x 2 mm²

= 220 mm²

कैप्सूल का पृष्ठीय क्षेत्रफल = 220 mm² उत्तर

7. कोई तंबू एक बेलन के आकार का है जिस पर एक शंकु अध्यारोपित है। यदि बेलनाकार भाग की ऊँचाई और व्यास क्रमशः 2.1 m और 4 m है तथा शंकु की तिर्यक ऊँचाई 2.8 m है तो इस तंबू को बनाने में प्रयुक्त कैनवस (canvas) का क्षेत्रफल ज्ञात कीजिए। साथ ही, ₹500 प्रति m² की दर से इसमें प्रयुक्त कैनवस की लागत ज्ञात कीजिए। (ध्यान दीजिए कि तंबू के आधार को कैनवस से नहीं ढका जाता है।)

हल : शंकु का व्यास = बेलन का व्यास

2R = 4 m

R = 2 m

शंकु की त्रिज्या = बेलन की त्रिज्या

बेलन की ऊँचाई (H) = 2.1 m

शंकु की तिर्यक ऊँचाई (L) = 2.8 m

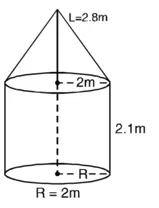
तंबू का वक्र पृष्ठीय क्षेत्रफल
= बेलन का वक्र पृष्ठीय क्षेत्रफल + शंक्वाकार भाग का वक्र पृष्ठीय क्षेत्रफल
= 2????RH + ????RL
= ????R [2H + L]

= 44 m² उत्तर

∴ तंबू का वक्र पृष्ठीय क्षेत्रफल = 44 m²
Im² कैनवस की लागत = ₹ 500
44 m² कैनवस की लागत = ₹ 44 x 500
= ₹ 22000
कैनवस की कुल लागत = ₹ 22000 उत्तर

8. ऊँचाई 2.4 cm और व्यास 1.4 cm वाले एक ठोस बेलन में से इसी ऊँचाई और इसी व्यास वाला एक शंक्वाकार खोल (cavity) काट लिया जाता है। शेष बचे ठोस का निकटतम वर्ग सेंटीमीटर तक पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

हल : बेलन का व्यास (D) = 1.4 cm
= शंकु का व्यास

∴ बेलन की त्रिज्या = शंकु की त्रिज्या (R) = 0.7 cm
बेलन की ऊँचाई (H) = 2.4 cm

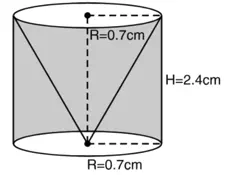
जैसा कि हम जानते हैं, L² = R² + H²

= √0.49 + 5.76 cm
= √6.25 cm
L = 2.5 cm

शेष बचे ठोस का संपूर्ण पृष्ठीय क्षेत्रफल

= बेलन का वक्र पृष्ठीय क्षेत्रफल
+ बेलन के आधार का क्षेत्रफल
+ शंकु का पृष्ठीय क्षेत्रफल
= 2????RH + ????R² + ²RL
= ????R [2R + R + L]

शेष बचे ठोस का निकटतम वर्ग सेंटीमीटर तक पृष्ठीय क्षेत्रफल = 18 cm² उत्तर

9. लकड़ी के एक ठोस बेलन के प्रत्येक सिरे पर एक अर्धगोला खोदकर निकालते हुए, एक वस्तु बनाई गई है, जैसा कि आकृति में दर्शाया गया है। यदि बेलन की ऊँचाई 10 cm है और आधार की त्रिज्या 3.5 cm है तो इस वस्तु का संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

हल : बेलन की ऊँचाई (H) = 10 cm
बेलन की त्रिज्या = अर्धगोले की त्रिज्या (R)
= 3.5 cm

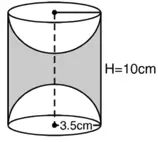
वस्तु का संपूर्ण पृष्ठीय क्षेत्रफल
= बेलन का वक्र पृष्ठीय क्षेत्रफल
+ 2 अर्धगोले का वक्र पृष्ठीय क्षेत्रफल
= 2????RH + 2 (2????R²)
= 2????R [H + 2R]

= 22 x 17 cm²
= 374 cm²

∴ वस्तु का संपूर्ण पृष्ठीय क्षेत्रफल

= 374 cm² उत्तर

इस पोस्ट में आपको Class 10 Maths NCERT Solutions Exercise 13.1 NCERT Solutions for Class 10 Maths Exercise 13.1 class 10 maths chapter 13 pdf Class 10 maths chapter 13 solutions Class 10 Maths Chapter 13 Surface Areas And Volumes Ex 13.1 questions with solutionsकक्षा 10 गणित एनसीईआरटी समाधान अध्याय 13 अभ्यास 13.1 पृष्ठीय क्षेत्रफल और आयतन एनसीईआरटी समाधान कक्षा 10 गणित प्रश्नावली 13.1 से संबंधित पूरी जानकारी दी गई है अगर इसके बारे में आपका कोई भी सवाल या सुझाव हो तो नीचे कमेंट करके हम से जरूर पूछें और अगर आपको यह जानकारी फायदेमंद लगे तो अपने दोस्तों के साथ शेयर जरूर करें.

Class 10 Maths Chapter 13. पृष्ठीय क्षेत्रफल और आयतन Exercise 13.1
Class 10 Maths Chapter 13. पृष्ठीय क्षेत्रफल और आयतन Exercise 13.2
Class 10 Maths Chapter 13. पृष्ठीय क्षेत्रफल और आयतन Exercise 13.3
Class 10 Maths Chapter 13. पृष्ठीय क्षेत्रफल और आयतन Exercise 13.4
Class 10 Maths Chapter 13. पृष्ठीय क्षेत्रफल और आयतन Exercise 13.5

NCERT Solutions For Class 10th Maths पृष्ठीय क्षेत्रफल और आयतन (प्रश्नावली 13.1)

Related Posts

Leave a Comment Cancel Reply