Class 8 Maths Chapter 9 – बीजीय व्यंजक एवं सर्वसमिकाएँ

NCERT Solutions Class 8 Maths Chapter 9 बीजीय व्यंजक एवं सर्वसमिकाएँ – जो विद्यार्थी 8 कक्षा में पढ़ रहे है एनसीईआरटी समाधान कक्षा 8 गणित अध्याय 9 यहाँ से प्राप्त करें .कक्षा 8 के छात्रों के लिए यहाँ पर गणित विषय के अध्याय 9 का पूरा समाधान दिया गया है। जो भी गणित विषय में अच्छे अंक प्राप्त करना चाहते है उन्हें यहाँ पर एनसीईआरटी समाधान कक्षा 8 गणित अध्याय 9. (बीजीय व्यंजक एवं सर्वसमिकाएँ) का पूरा हल मिल जायेगा। जिससे की छात्रों को तैयारी करने में किसी भी मुश्किल का सामना न करना पड़े। इस NCERT Solutions For Class 8th Maths Chapter 9 Algebraic Expressions and Identities की मदद से विद्यार्थी अपनी परीक्षा की तैयारी अच्छे कर सकता है और परीक्षा में अच्छे अंक प्राप्त कर सकता है.

Class	Class 8
Subject	Maths
Chapter	Chapter 9
Chapter Name	बीजीय व्यंजक एवं सर्वसमिकाएँ

NCERT Solutions For Class 8 गणित Chapter 9 बीजीय व्यंजक एवं सर्वसमिकाएँ

Class 8 Maths बीजीय व्यंजक एवं सर्वसमिकाएँ Ex 9.1
Class 8 Maths बीजीय व्यंजक एवं सर्वसमिकाएँ Ex 9.2
Class 8 Maths बीजीय व्यंजक एवं सर्वसमिकाएँ Ex 9.3
Class 8 Maths बीजीय व्यंजक एवं सर्वसमिकाएँ Ex 9.4
Class 8 Maths बीजीय व्यंजक एवं सर्वसमिकाएँ Ex 9.5

बीजीय व्यंजक एवं सर्वसमिकाएँ के बहुविकल्पीय प्रश्न

Class 8 गणित Chapter 9 बीजीय व्यंजक एवं सर्वसमिकाएँ (प्रश्नावली 9.1)

प्रश्न 1. निम्नलिखित व्यंजकों में से प्रत्येक के पदों एवं गुणांकों को पहचानिए
(i) 5xyz² – 3zy (ii) 1 + x + x² (iii) 4x²y²-4x²y²z² + z²
(iv) 3 – pq + qr – rp (v)

(vi) 0.3α – 0.6αb + 0.5b

हल :

	व्यंजक	पद	गुणांक
(i)	5xyz² – 3zy	5xyz² – 3zy	5 – 3
(ii)	1 + x + x²	1 x x²	1 1 1
(iii)	4x²y²z²+z²	4x²y² -4x²y²z²	4 – 4 1
(iv)	3 – pq + qr – rp	3 – pq qr – rp	3 – 1 1 – 1
(v)		– xy	– 1
(vi)	0.3α – 0.6αb + 0.5b	0.3α – 0.6 αb 0.5b	0.3 – 0.6 0.5

प्रश्न 2. निम्नलिखित बहुपदों को एकपदी, द्विपद एवं त्रिपद के रूप में वर्गीकृत कीजिए। कौन-सा बहुपद इन तीन श्रेणियों में से किसी में भी नहीं है?

x + y, 1000, x + x² + x³ + x⁴, 7 + y + 5x, 2y – 3y², 2y – 3y² + 4y³, 5x – 4y + 3xy, 4z – 15z², αb + bc + cd + dα, pqr,p²q + pq², 2p + 2q

हल : दिए गए बहुपदों के अनुसार –

(i) एकपदी – 1000, pqr
(ii) द्विपदी – x + y, 2y – 3y², 4z – 15z², p²q + pg², 2p + 2q
(iii) त्रिपदी – 7 + y + 5x, 2y – 3y² + 4y³, 5x – 4y + 3ry
(iv) वे बहुपद जो उपरोक्त श्रेणियों में नहीं आते हैं – x + x² + x³ + x⁴ αb + bc + cd + dα

प्रश्न 3. निम्नलिखित का योग ज्ञात कीजिए
(i) αb – bc, bc – cα, cα – αb
(ii) α – b + αb, b – c + bc,c – α + αc
(iii) 2p²q² – 3pq + 4,5 + 7pq – 3p²q²
(iv) l²+m²,m² + n²,n² + l²,21m + 2mn + 2nl

हल : दिए गए व्यंजकों के समान पदों को एक-दूसरे के नीचे लिखकर हम योग ज्ञात करेंगे

(i)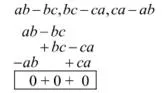

अतः योगफल = 0 उत्तर
(ii)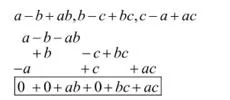

अतः योगफल = αb + bc + αc उत्तर
(iii)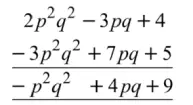

अतः योगफल = – p²q² + 4pq + 9 उत्तर
(iv)

अतः योगफल = 2l² + 2m² + 2n² + 2lm + 2mm + 2nl

= 2(l² + m² + n² + lm + mm + nl) उत्तर

प्रश्न 4. (a) 12α – 9αb + 5b – 3 में से 4α – 7αb + 3b + 12 को घटाइए।
(b) 5xy – 2yz – 2zx + 10xyz में से 3xy + 5yz – 7zx को घटाइए।
(c) 18 – 3p – 11q + 5pq – 2pg² + 5p²q में से 4p²q – 3pg + 5pq² – 8p + 7q-10 को घटाइए।

हल :घटाने के लिए दिए गए व्यंजकों के समान पदों को एक-दूसरे के नीचे लिखा जाएगा –

(a)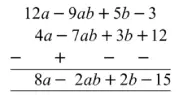

(b)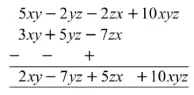

(c)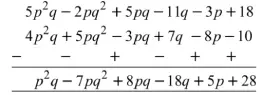

Class 8 गणित Chapter 9 बीजीय व्यंजक एवं सर्वसमिकाएँ (प्रश्नावली 9.2)

प्रश्न 1. निम्नलिखित एकपदी युग्मों का गुणनफल ज्ञात कीजिए

(i) 4,7p (ii) – 4p, 7p (iii) – 4p,7pq (iv) 4p³, – 3p (v) 4p,0

हल : (i) 4 x 7p = (4 x 7) x p = 28p उत्तर
(ii) – 4p x 7p = (- 4 x 7) x (p x p) = – 28p¹⁺¹
= – 28p² उत्तर
(iii) – 4p x 7pq = (- 4 x 7) x (p x p x q) = – 28p¹⁺¹q

= – 28p²q उत्तर
(iv) 4p³ x (- 3p) = [4 x (- 3)] x [p³ x p] = – 12p³⁺¹

= – 12p⁴ उत्तर
(v) 4p x 0 = (4 x 0) x p = 0 x p

= 0 उत्तर

प्रश्न 2. निम्नलिखित एकपदी युग्मों के रूप में लंबाई एवं चौड़ाई रखने वाले आयतों का क्षेत्रफल ज्ञात कीजिए (p,g); (10m, 5n); (20????²,5y²); (4????, 3????²); (3mn, 4np)

हल :हम जानते हैं कि आयत का क्षेत्रफल = लंबाई x चौड़ाई

दिए गए पदों के पहले पद को लंबाई तथा दूसरे पद को चौड़ाई मानते हुए हम आयतों का क्षेत्रफल पदों के गुणनफल द्वारा ज्ञात करेंगे।

(i) p और भुजाओं वाले आयत का क्षेत्रफल = p x q
= pq उत्तर

(ii) 10m और 5n भुजाओं वाले आयत का क्षेत्रफल = 10m x 5n

= (10 x 5) x (m x n)

= 50 mn उत्तर

(iii) 20????² और 5y² भुजाओं वाले आयत का क्षेत्रफल = 20????² x 5y²

= (20 x 5) x (????² x y²)

= 100 x²y² उत्तर

(iv) 4???? और 3????² भुजाओं वाले आयत का क्षेत्रफल = 4???? x 3????²

= (4 x 3) x (???? x ????²)

= 12 ????³ उत्तर

(v) 3mm और 4np भुजाओं वाले आयत का क्षेत्रफल = 3mm x 4np

= (3 x 4) x (m x n x n x p)
= 12 mn????²p उत्तर

प्रश्न 3. गुणनफलों की सारणी को पूरा कीजिए –

प्रथम एकपदी → द्वितीय एकपदी ↓	2????	– 5y	3????²	– 4????y	7????²y	– 9????²y²
2????	4????²	….	….	…..	….	…..
– 5y	…	….	– 15????²y	…..	…..	…..
3????²	….	…	…	…	…	…
– 4????y	….	…	…	…	…	…
7????²y	….	….	…	…	….	…
-9????²y²	…	…	…	…	….	…

हल :

प्रथम एकपदी → द्वितीय एकपदी ↓	2????	– 5y	3????²	– 4????y	7????²y	– 9????²y²
2????	4????²	-10????y	6????³	-8????²y	-14????³y	-18????³y²
– 5y	-10????y	25y²	– 15????²y	20????y²	-35????²y²	45????²y²
3????²	6????³	-15????²y	9????⁴	-12????³y	21????⁴y	– 27????⁴y²
– 4????y	– 8????²y	20????y²	-12³y	16????²y²	-28????³y²	36????³y³
7????²y	14????³y	– 35????²y²	21????⁴y	-28????³y²	49????⁴y²	-63????⁴y³
-9????²y²	– 18????³y²	45????²y³	-27????²y³	36????³y³	-63????⁴y³	81????⁴y⁴

प्रश्न 4. ऐसे आयताकार बक्सों का आयतन ज्ञात कीजिए जिनकी लंबाई, चौड़ाई और ऊँचाई क्रमशः निम्नलिखित हैं –
(i) 5α, 3α²,7α⁴
(ii) 2p, 4q, 8r
(iii) xy, 2????²y, 2????y²
(iv) α, 2b, 3c

हल : हम जानते हैं कि आयताकार बक्सों का आयतन = लंबाई x चौड़ाई x ऊँचाई
अतः दिए गए पदों के गुणनफल से हमें आयताकार बक्सों का आयतन प्राप्त होगा

(i) वांछित आयतन = 5α x 3α² x 7α⁴

= (5 x 3 x 7)x (α x α² x α⁴)

= 105α¹⁺²⁺⁴ = 105α⁷ उत्तर

(ii) वांछित आयतन = 2p x 4q x 8r
= (2 x 4 x 8) x (p x q x r)

= 64pqr उत्तर

(iii) वांछित आयतन = ????y x 2????²y x 2xy²

= (1 x 2 x 2) x (???? x ????² x ???? x y x y x y²)

= 4????¹⁺²⁺¹y^{1 + 1 + 2} = 4????⁴y⁴ उत्तर

(iv) वांछित आयतन = α x 2b x 3c
= (1 x 2 x 3) x (α x b x c)
= 6 αbc उत्तर

प्रश्न 5. निम्नलिखित का गुणनफल ज्ञात कीजिए –
(i) xy,yz, zx (ii) α,- α², α³ (iii) 2, 4y, 8y², 16y³ (iv) α, 2b, 3c, 6abc (v) m,-mn, mnp

हल : (i) ????y, yz और z???? का गुणनफल = ????y x yz x z????
= ???? x ???? x y x y x z x z
= ????² y² z² उत्तर

(ii) α,- α² और α³ का गुणनफल = α x (- α) x α³

= [1 x (- 1) x 1] x (α x α² x α³] = – 1 α^{1 + 2 + 3}
= -1α⁶ उत्तर

(iii) 2,4y, 8y² और 16y³ का गुणनफल = 2 x 4y x 8y² x 16y³

= (2 x 4 x 8 x 16) (y x y² x y²)

= 1024 y¹⁺²⁺³ = 1024y⁶ उत्तर

(iv) α, 2b,3c तथा 6αbc का गुणनफल = α x 2b x 3c x 6αbc
= (1 x 2 x 3 x 6) (α x α x b x b x c x c)
= 36α¹⁺¹ b¹⁺¹ c¹⁺¹ = 36α²b²c² उत्तर

(v) m, – mm और mmp का गुणनफल = m x (- mm) x mmp

= [1 x (- 1) x 1] x (m x m x m x n x n x p)
= – 1m¹⁺¹ n¹⁺¹ .nl+1.pl
= -1 m?np UTRE

Class 8 गणित Chapter 9 बीजीय व्यंजक एवं सर्वसमिकाएँ (प्रश्नावली 9.3)

प्रश्न 1. निम्नलिखित युग्मों में प्रत्येक के व्यंजकों का गुणन कीजिए
(i) 4p, q + r (ii) ab,a-b (iii) a+b,7α²b²
(iv) α² – 9,4a (v) pq + qr + rp,0

हल : (i) 4p x (q + r) = 4p x q + 4p x r = 4pq + 4pr उत्तर

(ii) αb x (α – b) = αb x α – αb x b = α²b – αb² उत्तर

(iii) (α + b) x 7α² – b² = α x 7α²b² + b x 7α²b²

= 7α³b² + 7α²2b³ उत्तर
(iv) (α² – 9) x 4α = 4α x α² – 4α x 9

= 4α³ – 36α उत्तर

(v) (pq + qr + rp) x 0 = 0 उत्तर

प्रश्न 2. सारणी को पूरा कीजिए –

	प्रथम व्यंजक	द्वितीय व्यंजक	गुणनफल
(i) (ii) (iii) (iv) (v)	α ???? + y – 5 p 4p²q² α + b + c	b + c + d 5 ????y 6p² – 7p + 5 p² – q² αbc	…….. …….. …….. ……… ……….

हल :(i) α x (b + c + d) = α x b + α x c + α x d

= αb+ αc + αd उत्तर

(ii) (???? + y – 5) x 5????y = ???? x 5????y + y x 5????y – 5 x 5????y

= 5????²y + 5????y² – 25????y उत्तर

(iii) p x (6p² – 7p + 5) = p x 6p² – p x 7p + p x 5

= 6p³ – 7p² + 5p उत्तर

(iv) 4p²q²x (p² – q²) = 4p² – q² x p² – 4p²q² x q²

= 4p⁴q² – 4p²q⁴ उत्तर
(v) (α + b + c) x αbc = α x αbc + b x αbc + c x αbc

= α²bc + αb²c + abc² उत्तर

प्रश्न 3. गुणनफल ज्ञात कीजिए

(i) (α² x (2α²²) x (4α²⁶)

(ii)

(iii)

(iv) ???? x ????² x ????³ x ????⁴

हल : (i) (α²) x (2α²²) x (4α²⁶) = (1 x 2 x 4) x (α² x α²² x α²⁶)
= 8α^2+22+26 + 8α⁵⁰ उत्तर

(ii)

(iii)
= – 4p¹⁺³ q³⁺¹
= – 4p⁴ q⁴
(iv) ???? x ????² x ????³ x ????⁴ = ????^1+2+3+4 = ????¹⁰ उत्तर

प्रश्न 4. (a) 3???? (4???? – 5) + 3 को सरल कीजिए और (i) ???? = 3 एवं (ii) Simple! This is an alert message. के लिए इसका मान ज्ञात कीजिए।
(b) α(α² + α + 1) + 5 को सरल कीजिए और (i) α = 0, (ii) α = 1 एवं (ii) α = – 1 के लिए इसका मान ज्ञात कीजिए।

हल : (a) 3???? (4???? – 5) + 3 = 3???? x 4???? – 3???? x 5 + 3

= 12????² – 15???? + 3 उत्तर
(i) ???? = 3 के लिए 12????² – 15???? + 3 = 12 (3)² – 15 (3) + 3

= 12 x 9 – 45 + 3 = 108 – 45 + 3
= 111 – 45 = 66 उत्तर

(ii) के लिए 12????² – 15???? + 3 =

उत्तर

(b) α(α² + α + 1) + 5 = α x α² + α x α + α x 1 + 5
= α³ + α² + α + 5 उत्तर
(i) α = 0 के लिए α³ + α² + α + 5 = (0)³ + (0)² + 0 + 5

= 0 + 0 + 0 + 5 = 5 उत्तर

(ii) α = 1 के लिए α³ + α² + α + 5 = (1)³ + (1)² + (1) + 5

= 1 + 1 + 1 + 5 = 8 उत्तर
(iii) α = -1 के लिए α³ + α² + α + 5 = (-1)³ + (-1)² + (- 1) + 5

= – 1 + 1 – 1 + 5 = 6 – 2 = 4 उत्तर

प्रश्न 5. (a) p (p – q), q(q – r) एवं r (r – p) को जोडिए।
(b) 2???? (z – ???? – y) एवं 2y (z – y – ????) को जोड़िए।
(c) 4l (10n – 3m + 2l) में से 3l (l – 4m + 5n) को घटाइए।
(d) 4c ( – α + b + c) में से 3α (α + b + c) – 2b (α – b + c) को घटाइए।

हल : (a) p(p – q) + q (q – r) + r (r – p) = p x p – p x q + q x q – q x r + r x r – p x r

= p² – pq + q² – qr + 2² – pr

= p² + q² + r² – pq – qr – pr उत्तर

(b) 2???? (z – ???? – y) + 2y (z – y – x) = 2???? x z – 2???? x ???? – 2???? x y + 2y x z – 2y x y – 2y x ????
= 2????z – 2????² – 2xy + 2yz – 2y² – 2yx
= – 2????² – 2y² – 4xy + 2yz + 2zx उत्तर

(c) 4l (10n – 3m + 2l) – 3l (l – 4m + 5n) = 4l x 10n – 4l x 3m + 4l x 2l – 3l x l + 3l x 4m – 3l x 5n
= 40ln – 12lm + 8l² – 3l² + 12lm – 15In
= 8l² – 3l² + 40ln – 15ln – 12lm + 12lm
= 5l² + 25In उत्तर

(d) 4c (- α + b + c) – [3α (α + b + c) – 2b (c – b + c)] = 4c (- α + b + c) – 3α (α + b + c) + 2b (α – b + c)
= – 4αc + 4bc + 4c² – 3α² – 3αb – 3αc + 2αb – 2b²
= – 3α² – 2b² + 4c² + (- 3αb + 2αb) + (4bc + 2bc) + (- 4αc – 3αc)
= – 3α² – 2b² + 4c² – αb + 6bc -7αc उत्तर

Class 8 गणित Chapter 9 बीजीय व्यंजक एवं सर्वसमिकाएँ (प्रश्नावली 9.4)

प्रश्न 1. द्विपदों को गुणा कीजिए –
(i) (2???? + 5) और (4???? – 3) (ii) (y – 8) और (3y – 4) (iii) (2.5l – 0.5m) और (2.5l + 0.5m)
(iv) (α + 3b) और (???? + 5) (v) (2pg + 3g²) और (3pg – 2q²)
(vi)

और

हल : (i) (2???? + 5) x (4???? – 3) = 2???? x (4???? – 3) + 5 x (4???? – 3)

= 8????² – 6???? + 20???? – 15
= 8????² + 14???? – 15 उत्तर

(ii) (y – 8) x (3y – 4) = y x (3y – 4) – 8 x (3y – 4)
= 3y² – 4y – 24y + 32
= 3y² – 28y + 32 उत्तर

(iii) (2.5l – 0.5m) x (2.5l + 0.5m) = 2.51 x (2.51 + 0.5m) – 0.5m x (2.51 + 0.5m)

= 6.25l² + 1.25lm – 1.25lm – 0.25m²
= 6.25l² – 0.25m² उत्तर

(iv) (α + 3b) x (???? + 5) = ???? x (???? + 5) + 3b x (???? + 5)
= α???? + 5???? + 3b???? + 15b उत्तर

(v) (2pq + 3q²) x (3pq – 2q²) = 2pq x (3pq – 2q²) + 3q² x (3pq – 2q²)

= 6p²q² – 4 pq³ + 9pq² – 6q⁴
= 6p²q² + 5pq³ – 6q⁴ उत्तर

(vi)

= 3α⁴ – 2α² b² + 12α²b² – 8b⁴

= 3α⁴ + 10α² b² – 8b⁴ उत्तर

प्रश्न 2. गुणनफल ज्ञात कीजिए –
(i) (5 – 2????) (3 + ????) (ii) (???? + 7y) (7???? – y) (iii) (α² + b) (α + b²)
(iv) (p² -q²) (2p + q)

हल : (i) (5 – 2????) (3 + ????) = 5 x (3 + ????) – 2???? x (3 + ????)
= 15 + 5???? – 6???? – 2 x 2
= – 2????² – ???? + 15 उत्तर

(ii) (???? + 7y) (7???? – y) = ???? x (7???? – y) + 7y x (7x – y)
= 7????² – ????y + 49????y -7y²
= 7????² + 48????y – 7y² उत्तर

(iii) (α² + b) (α + b²) = α² x (α + b²) + b x (α + b²)
= α³ + α²b² + αb + b³ उत्तर

(iv) (p² – q²) (2p + q) = p² x (2p + q) – q² – (2p + q)

= 2p³ + p²q – 2pq – q³ उत्तर

प्रश्न 3. सरल कीजिए
(i) (x² – 5) (x + 5) + 25
(ii) (α² + 5) (b³ + 3) + 5
(iii) (t + s²) (t² – s)
(iv) (α + b) (c – d) + (α – b) (c + d) + 2 (αc + bd)
(v) (???? + y) (2???? + y) + (???? + 2y) (???? – y)
(vi) (???? + y) (????² – ????y + y²)
(vii) (1.5???? – 4y) (1.5???? + 4y + 3) – 4.5???? + 12y
(viii) (α + b + c) (α + b – c)

हल :(i) (????² – 5) (???? + 5) + 25 = ????² x (???? + 5) – 5 x (???? + 5) + 25
= ????³ + 5????² – 25 + 25
= ????³ + 5????² – 5???? उत्तर

(ii) (α² + 5) (b³ + 3) + 5 = α² x (b³ + 3) + 5 x (b³ + 3) + 5

= α²b³ + 3α² + 5b³ + 15 + 5
= α²b³ + 3α² – + 5b³ + 20 उत्तर

(iii) (t + s²) (t² – s) = t x (t² – s) + s² x (t² – s)
= t² – ts + t²s² – s² उत्तर

(iv) (α+b) (c-d) + (α-b) (c+d)+2(αc + bd)
= α(c-d)+ b(c-d)+ α(c+d)-b(c+d)+2αc +2bd
= αc-αd + bc-bd + αc+ αd-bc – bd+2αc +2bd
= (αc+αc +2αc) + (-αd + αd) + (bc – bc)+ (-bd – bd + 2bd)
= 4αc+0+0+0=4αc उत्तर

(v) (????+y) (2???? +y) + (???? +2y) (????-y) = ???? (2???? + y) + y (2???? +y) + ???? (????-y)+2y (x-y)
= 2????² + ????y + 2????y + y² +????² – ????y + 2????y – 2y²
= (2????² + ????²) + (????y + 2????y – ????y + 2????y) + (y²-2y²)
= 3????² + 4????y – y² उत्तर

(vi) (???? + y) (????² – ????y + y²) = ????(????² – ????y + y²) + y (????² – ????y + y²)
= ????³ – ????²y + ????y² + ????²y – ????y² + y³
= ????³ + (- ????²y + ????²y) + (????y² – ????y²) + y²
= ????³ + 0 + 0 + y³ = ????³ + y³ उत्तर

(vii) (1.5???? – 4y) (1.5???? + 4y + 3) – 4.5???? + 12y = 1.5???? (1.5???? + 4y + 3) – 4y (1.5???? + 4y + 3) – 4.5???? + 12y

= 2.25????² + 6.0 ????y + 4.5???? – 6.0????y-16y² – 12y – 4.5???? + 12y
= 2.25????² + (6????y – 6????y) + (4.5???? – 4.5????) – 16y² + (-12y + 12y)
= 2.25????² + 0 + 0 – 16y² + 0 = 2.25????² – 16y² उत्तर

(viii) (α + b + c) (α + b – c) = α(α + b – c) + b(α + b – c) + c (a + b – c)

= α² + αb – αc + αb + b2- bc + αc + bc – 2
= α² + b² – c² + (αb + αb) + (- bc + bc) + (- αc + αc)

= α² + b²– c² + 2αb + 0 + 0 = α² + b²-c² +2αb उत्तर

Class 8 गणित Chapter 9 बीजीय व्यंजक एवं सर्वसमिकाएँ (प्रश्नावली 9.5)

प्रश्न 1. निम्नलिखित गुणनफलों में से प्रत्येक को प्राप्त करने के लिए उचित सर्वसमिका का उपयोग कीजिए

(i) (???? + 3) (???? + 3)

(ii) (2y + 5) (2y + 5)

(iii) (2α – 7) (2α – 7)
(iv)
(v) (1.1m – 0.4) (1.1m + 0.4)
(vi) (α² + b²) (- α² + b²)
(vii) (6???? – 7) (6???? + 7)
(viii) (- α + c) (- α + c)
(ix)
(x) (7α – 9b) (7α – 9b)

हल :

(i) (???? + 3) (???? + 3) = (???? + 3)²
= (????)² + 2 x ???? 3 + (3)² [∵ (α + b)² = α² + 2αb + b²] = ????² + 6???? + 9 उत्तर

(ii) (2y + 5) (2y + 5) = (2y + 5)²
= (2y)² + 2 x 2y x 5 + (5)² [∵ (α + b)² = α² + 2αb + b²]

= 4y² + 20y + 25 उत्तर

(iii) (2α – 7) (2α – 7) = (2α – 7)²
= (2α)² – 2 x 2α x 7 + (7)² [∵ (α – b)² = α² – 2αb + b²] = 4α² – 28α + 49 उत्तर

(iv)

[∵ (α – b)² = α² – 2αb + b²]

= उत्तर

(v) (1.1m – 0.4) (1.1m + 0.4) = (1.1m)² – (0.4)²

[∵ (α – b) (α + b) = α² – b²] = 1.21m² – 0.16 उत्तर

(vi) (α² + b²) (- α² + b²) = (b² + α²) (b² – α²)
[∵ (α – b) (α + b) = α² – b²] = (b²)² – (α²)²

= b⁴ – α⁴ उत्तर

(vii) (6???? – 7) (6???? + 7) = (6????)² – (7)²

[∵ (α – b) (α + b) = α² – b²] = 36????² – 49 उत्तर

(viii) (-α + c) (-α + c) = (c – α) (c – α)
= (c – α)²
= (c)² – 2 x c x α + (α)²
[∵ (α – b)² = α² – 2αb + b²]

= c² – 2αc + α² उत्तर

(ix)

[∵ (α + b)² = α² + 2αb + b²]

उत्तर

(x) (7α – 9b) (7α – 9b) = (7α – 9b)²
= (7α)² – 2 x 7α x 9b + (9b)²

[∵ (α – b)² = α – 2αb + b² ]

= 49α²-126αb + 81b² उत्तर

प्रश्न 2. निम्नलिखित गुणनफलों को ज्ञात करने के लिए सर्वसमिका (???? + α) (???? + b) = ???? + (α + b) ???? + αb का उपयोग कीजिए

(i) (???? + 3) (???? + 7) (ii) (4???? + 5) (4???? + 1) (iii) (4???? – 5) (4???? – 1)
(iv) (4???? + 5) (4???? -1) (v) (2???? + 5y) (2???? + 3y) (vi) (2α² + 9) (2α² + 5)
(vii) (????yz – 4) (????yz – 2)

हल : (i) (???? + 3) (???? + 7) = ????² + (3 + 7)???? + 3 x 7
= ????² + 10???? + 21 उत्तर

(ii) (4???? + 5) (4???? + 1) = (4????)² + (5 + 1) x 4???? + 5 x 1
= 16????² + 24???? + 5 उत्तर

(iii) (4???? – 5) (4???? – 1) = [4???? + (-5)] [4???? + (-1)]

= (4????)² + (- 5 – 1) x 4???? + (- 5) x (-1)
= 16????² – 24???? + 5 उत्तर

(iv) (4???? + 5) (4???? – 1) = (4???? + 5) [4???? + (-1)] = (4????)² + (5 – 1) x 4???? + 5 x (- 1)
= 16????² + 16???? – 5 उत्तर

(v) (2???? + 5y) (2???? + 3y) = (2????)² + (5y + 3y) x 2???? + 5y x 3y
= 4????² + 16????y + 15y² उत्तर
(vi) (2α² + 9) (2α² + 5) = (2α²)² + (9 + 5) x 2α² + 9 x 5
= 4α⁴ + 28α² + 45 उत्तर

(vii) (????yz – 4) (????yz – 2) = [????yz + (- 4)] [????yz + (-2)] = (xyz)² + (- 4 – 2) x ????yz + (- 4) ( – 2)
= ????²y²z² – 6????yz + 8 उत्तर

प्रश्न 3. सर्वसमिका का उपयोग करते हुए निम्नलिखित वर्गों को ज्ञात कीजिए
(i) (b – 7)² (ii) (????y + 3z)² (iii) (6????² – 5y)²
(iv)

(v) (0.4p – 0.5q)²
(vi) (2????y + 5y)²

हल :(i) (b – 7)² = (b)² – 2 x b x 7 + (7)²

= b² – 14b + 49 उत्तर
(ii) (????y + 3z)² = (????y)² + 2 x ????y x 3z + (3z)²

(iii) (6????² – 5y²) = (6????²)² – 2 x 6????² x 5y + (5y)²
= 36????⁴ – 60????²y+25y²उत्तर
(iv)

(v) (0.4p – 0.5q)² = (0.4p)² – 2 x (0.4p) x (0.5q) + (0.5q)²
= 0.16p² – 0.4pq + 0.25q² उत्तर
(vi) (2????y + 5y)² = (2????y)² + 2 x 2????y x 5y + (5y)²
= 4????²y² + 20????y² + 25y² उत्तर

प्रश्न 4. सरल कीजिए –
(i) (α² – b²)²
(ii) (2???? + 5)² – (2???? – 5)²
(iii) (7m – 8n)² + (7m + 8n)²
(iv) (4m + 5n)² + (5m + 4n)²
(v) (2.5p – 1.5q)² – (1.5p – 2.5q)²
(vi) (αb + bc)² – 2αb²c
(vii) (m² – n²m)² + 2m²n²

हल : (i) (α² – b²)² = (α²)² – 2 x α² x b² + (b²)²
= α⁴ – 2α²b² + b⁴ उत्तर

(ii) (2???? + 5)² – (2???? – 5)² = [(2????)² + 2 x 2???? x 5 + (5)²] – [(2????)² – 2 x 2???? x 5 + (5)²] = [4????² + 20???? + 25] – [4????² – 20???? + 25] = 4????² + 20???? + 25 – 4????² + 20???? – 25
= 40???? उत्तर

(iii) (7m – 8n)² + (7m + 8n)² = [(7m)² – 2 x 7m x 8n + (8n)²] + [(7m)² + 2 x 7m x 8n + (8n)²] = [49m² – 112mm + 64n²] + [49m² + 112mm + 64n²] = 49m² – 112mm + 64n² + 49m² + 112mn + 64n²
= 98m² + 128n² – उत्तर
(iv) (4m + 5n) + (5m + 4n)² = [(4m)² + 2 x 4m x 5n + (5n)²] + [(5m)² + 2 x 5m x 4n + (4n)²] = 16m + 40mm + 25n² + 25m² + 40mm + 16n²
= 41m² + 80mm + 41n² उत्तर

(v) (2.5p – 1.5q)² – (1.5p – 2.5q)² = [(2.5p)² – 2 x 2.5px 1.5q + (1.5q)²] – [(1.5p)² – 2 x 1.5p x 2.5q + (2.5q)²] = [6.25p² – 7.5pq + 2.25q²] – [2.25p² – 7.5pq + 6.25q²] = 6.25p² – 7.5pq + 2.25q² – 2.25p² + 7.5pq – 6.25q²
= 4p² – 4q² उत्तर

(vi) (αb + bc)² – 2αb²c = (αb)² + 2 x αb x bc + (bc)² – 2αb²c
= α²b² + 2αb²c + b²c² – 2αb²c
= α²b² + b²c² उत्तर
(vii) (m² – n²m)² + 2m³n² = (m²)² – 2 x m² x n²m + (n²m)² + 2m³n²

= m⁴ – 2m³n² + n⁴m + 2m³n²
= m⁴ + n⁴m² उत्तर

प्रश्न 5. दर्शाइए कि –
(i) (3???? + 7)² – 84???? = (3???? – 7)²
(ii) (9p – 5q)² + 180pq = (9p + 5q)²
(iii)

(iv) (4pq + 3q)² – (4pq – 3q)² = 48pq²
(v) (α – b) (α + b) + (b – c) (b + c) + (c – α) (c + α) = 0

हल : (i) बायाँ पक्ष = (3???? + 7)² – 84????
= (3????)² + 2 x 3???? x 7+ (7)² – 84????
= 9????² + 42???? + 49 – 84????
= 9????² – 42???? + 49
= (3????)² – 2 x 3???? x 7+ (7)²

= (3???? – 7)² = दायाँ पक्ष

(ii) बायाँ पक्ष = (9p – 5q)² + 180pq

= (9p)² – 2 x 9p x 5q + (5q)² + 180pq
= 81p² – 90pq + 25q² + 180pq
= 81p² + 90pq + 25q²
= (9p)² + 2 x 9p x 5q + (5q)²
= (9p + 5q)² = दायाँ पक्ष

(iii) बायाँ पक्ष

(iv) बायाँ पक्ष = (4pq + 3q)² – (4pq – 3q)²
= [(4pq)² + 2 x 4pq x 3q + (3q)²] – [(4pq)² – 2 x 4pq x 3q+ (3q)²] = [16p²q² + 24pq² + 9q²] – [16p²q² – 24pg² + 9q²] = 16p²q² + 24pq² + 9q² – 16p²q² + 24pq² – 9q²
= 48pq² = दायाँ पक्ष

(v) बायाँ पक्ष = (α – b) (α + b) + (b – c) (b + c) + (c – α) (c + α)
= α² – b² + b² – c² + c² – α²

= 0 = दायाँ पक्ष

प्रश्न 6. सर्वसमिकाओं के उपयोग से निम्नलिखित मान ज्ञात कीजिए –
(i) 71² (ii) 99² (iii) 102² (iv) 998² (v) 5.2²
(vi) 297 x 303 (vii) 78 x 82 (viii) 8.9² (ix) 1.05 x 9.5

हल : (i) 71² = (70 + 1)²
= (70)² + 2 x 70 x 1 + (1)²
= 4900 + 140 + 1 = 5041 उत्तर

(ii) 99² = (100 – 1)²
= (100)² – 2 x 100 x 1 + (1)²
= 10000 – 200 + 1
= 10001 – 200 = 9801 उत्तर

(iii) 102² = (100 + 2)²
= (100) + 2x 100 x 2 + (2)2
= 10000 + 400 + 4 = 10404 उत्तर

(iv) 998² = (1000 – 2)²
= (1000)² – 2 x 1000 x 2 + (2)²
= 1000000 – 4000 + 4
= 1000004 – 4000 = 996004 उत्तर

(v) 5.2² = (5 + 0.2)²
= (5)² + 2 x 5 x 0.2 + (0.2)²
= 25 + 2 + 0.04 = 27.04 उत्तर

(vi) 297 x 303 = (300 – 3) (300 + 3)
= (300)² – (3)²
= 90000 – 9 = 89991 उत्तर

(vii) 78 x 82 = (80 – 2) (80 + 2)
= (80)² – (2)²
= 6400 – 4 = 6396 उत्तर

(viii) (8.9)² = (9 – 0.1)²
= (9)² – 2 x 9 x 0.1 + (0.1)²
= 81 – 1.8 + 0.01 = 79.21 उत्तर

(ix) 1.05 x 9.5 = (1 + 0.05) x 9.5
= 1 x 9.5 + 0.05 x 9.5
= 9.5 + 0.475 = 9.975 उत्तर

प्रश्न 7. α² – b² = (α + b) (α – b) का उपयोग करते हुए निम्नलिखित मान ज्ञात कीजिए –
(i) 51² – 49² (ii) (1.02)² – (0.98)²
(iii) 153² – 147² (iv) 12.1² – 7.9²

हल : (i) (51)² – (49)² = (51 + 49) (51 – 49)

= 100 x 2 = 200 उत्तर
(ii) (1.02)² – (0.98)² = (1.02 + 0.98) (1.02 – 0.98)

= 2.00 x 0.04 = 0.08 उत्तर

(iii) (153)² – (147)² = (153 + 147) (153 – 147)
= 300 x 6 = 1800 उत्तर
(iv) (12.1)² – (7.9)² = (12.1 +7.9) (12.1-7.9)

= 20.0 x 4.2 = 84 उत्तर

प्रश्न 8. (???? + α) (???? + b) = ????² + (α + b) ???? + αb का उपयोग करते हुए निम्नलिखित मान ज्ञात कीजिए –
(i) 103 x 104 (ii) 5.1 x 5.2
(iii) 103 x 98 (iv) 9.7 x 9.8

हल : (i) 103 x 104 = (100 + 3) (100 + 4)
= (100)² + (3 + 4) x 100 + 3 x 4
= 10000 + 700 + 12 = 10712 उत्तर

(ii) 5.1 x 5.2 = (5 + 0.1) (5 + 0.2)
= (5)² + (0.1 + 0.2) x 5 + 0.1 x 0.2
= 25 + 1.5 + 0.02 = 26.52 उत्तर

(iii) 103 x 98 = (100 + 3) [100 + (-2)] = (100)² + (3 – 2) x 100 + 3 x (-2)
= 10000 + 100 – 6 = 10100-6 = 10094 उत्तर

(iv) 9.7 x 9.8 = (9 + 0.7) (9 + 0.8)
= (9)² + (0.7 + 0.8) x 9 + 0.7 x 0.8
= 81 + 13.5 + 0.56 = 95.06 उत्तर

इस पोस्ट में आपको Class 8 Maths (गणित) Chapter 9 बीजीय व्यंजक एवं सर्वसमिकाएँ बीजीय व्यंजक एवं सर्वसमिकाएँ Class 8th एनसीईआरटी समाधान कक्षा 8 गणित अध्याय 9 बीजीय व्यंजक एवं सर्वसमिकाएँ Class 8 Maths Chapter 9 Algebraic Expressions And Identities class 8 maths exercise 9.4 solutions algebraic expressions and identities class 8 pdf Ch 9 Algebraic Expressions and Identities Full Ex 9.3 || Ch 9 बीजीय व्यंजक एवं सर्वसमिकाएँ से संबंधित काफी महत्वपूर्ण जानकारी दी गई है यह जानकारी फायदेमंद लगे तो अपने दोस्तों के साथ शेयर करें और इसके बारे में आप कुछ जानना यह पूछना चाहते हैं तो नीचे कमेंट करके अवश्य पूछे.

NCERT Solutions For Class 8 गणित Chapter 9 बीजीय व्यंजक एवं सर्वसमिकाएँ

Class 8 गणित Chapter 9 बीजीय व्यंजक एवं सर्वसमिकाएँ (प्रश्नावली 9.1)

Class 8 गणित Chapter 9 बीजीय व्यंजक एवं सर्वसमिकाएँ (प्रश्नावली 9.2)

Class 8 गणित Chapter 9 बीजीय व्यंजक एवं सर्वसमिकाएँ (प्रश्नावली 9.3)

Class 8 गणित Chapter 9 बीजीय व्यंजक एवं सर्वसमिकाएँ (प्रश्नावली 9.4)

Class 8 गणित Chapter 9 बीजीय व्यंजक एवं सर्वसमिकाएँ (प्रश्नावली 9.5)

Related Posts

Leave a Comment Cancel Reply