Class 10 Maths Chapter 8 Exercise 8.4 – त्रिकोणमिति का परिचय

Class 10 Maths Chapter 8 Exercise 8.4 – त्रिकोणमिति का परिचय

NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.4 – जो विद्यार्थी 10वीं कक्षा में पढ़ रहे है उनके लिए यहां पर एनसीईआरटी कक्षा 10 गणित अध्याय 8. (त्रिकोणमिति का परिचय) प्रश्नावली 8.4 के लिए सलूशन दिया गया है. जोकि एक सरल भाषा में दिया है .ताकि विद्यार्थी को पढने में कोई दिक्कत न आए .इसकी मदद से आप अपनी परीक्षा में अछे अंक प्राप्त कर सकते है. इसलिए निचे आपको एनसीईआरटी समाधान कक्षा 10 गणित अध्याय 8 त्रिकोणमिति का परिचय प्रश्नावली 8.4 दिया गया है .

NCERT Solutions For Class 10th Maths त्रिकोणमिति का परिचय (प्रश्नावली 8.4)

हल : सर्वसमिका का प्रयोग करने पर,

cosec² A – cot² A = 1
⇒ cosec² A = 1 + cot² – A
⇒ (cosec A)² = cot² – A + 1

⇒

⇒

⇒

हम न्यून कोण A के लिए sin A के ऋणात्मक मानों को छोड़ देते हैं।

अतः,

सर्वसमिका का प्रयोग करने पर,

sec² – A – tan² – A = 1

⇒ sec² A = 1 + tan² A

⇒

हल : सर्वसमिका का प्रयोग करने पर,

sin² A + cos² A = 1

⇒ sin² – A = 1 – cos²A

⇒

⇒

[न्यून कोण A के लिए ऋणात्मक मान को छोड़ दीजिए]

⇒

1 + tan² A = sec² – A

tan² – A = sec² A – 1

(tan A)² = sec² A – 1

⇒ tan A = ± √sec² A – 1

[न्यून कोण A के लिए ऋणात्मक मान को छोड़ दीजिए]

अर्थात् tan A = ± √sec² A – 1

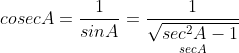
(i)

(ii) sin 25° cos 65° + cos 25° sin 65°

हल : (i)

=

[∵ sin (90° – θ) = cos θ] [and cos (90° – θ) = sin θ]

(ii) sin 25° cos 65° + cos 25° sin 65°

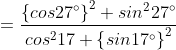
= sin 25° x cos (90° – 25°) + cos 25° x sin (90° – 25°)

= sin 25° x sin 25° + Cos 25° x cos 25°

[∵ cos(90° – θ) = sin θ] [ sin(90° – θ) = cos 0]

= sin²25+cos²25

= 1

(i) 9 sec² A – 9 tan² A =

(a) 1 (b) 9

(c) 8 (d) 0

(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ) =

(a) 0 (b) 1

(c) 2 (d) – 1

(iii) (sec A + tan A) (1 – sin A) =

(a) sec A (b) sin A

(c) cosec A (d) cos A

(iv)

(a) sec² – A (b) – 1

(c) cot² – A (d) tan² A

हल : (i) मान लो, 9 sec² A – 9 tan² – A

= 9 (sec²A – tan² – A)

= 9 x 1 = 9.

सही विकल्प (b) है।

(ii) मान लो (1 + tan θ + sec θ) (1 + cot θ – cosec θ)

[∵ (α + b) (α – b) = α² – b²]

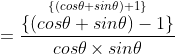
∴ सही विकल्प (c) है।

(iii) मान लो, (sec A + tan A) (1 – sin A)

[∵ cos² A = 1 – sin²A]

= cos A

∴ सही विकल्प (d) है।

(iv) मान लो,

∴ सही विकल्प (d) है।

(i)

(ii)

(iii)

[संकेत : व्यंजकों को sin e और cos e के पदों में लिखिए]

(iv)

[संकेत : LHS और RHS को अलग-अलग सरल कीजिए]

(v)

सर्वसमिका cosec² A = 1 + cot² A को लागू करके

(vi)

(vii)

(viii) (sin A + cosec A)² + (cos A + sec A)² = 7 + tan² A + cot² A

(ix) (cosec A – sin A) (sec A – cos A)

[संकेत : LHS और RHS को अलग – अलग सरल कीजिए]

हल: LHS = (cosec θ – cot θ)²

सर्वसमिका sin²θ + cos² θ = 1 का प्रयोग करने

⇒ sin² 0 = 1 – cos² 0

[∵ α² – b² = (α + b) (α – b)]

∴ LHS = RHS

अंत:,

(ii)

[∵ (a – b² = (a² + b²) (2ab)]

∴ LHS = RHS

अंत:,

(iii)

[∵ α³ – b³ = (α – b) (α² + b²+ αb)]

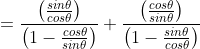
= 1 + sec θ cosec θ

∴ LHS = RHS

अंत;,

(iv)

= 1 + cos A ….(1)

[∵ 1 – cos²A=sin²A]

= 1 + cos A ….(2)

(1) और (2) से स्पष्ट है

LHS = RHS

अंत:,

(v)

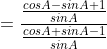
= cosec A + cot A

∴ LHS = RHS

अंत:,

(vi)

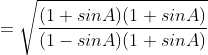
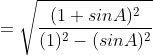
= sec A + tan A

∴ LHS = RHS

अंत:,

(vii)

∴ LHS = RHS

अंत;,

(viii) LHS =(sin A + cosec A)² + (cos A + sec A)²

= {sin² A + cosec² A + 2 sin A x cosec A} + {cos² A + sec² A + 2 cos A x sec A}

= {sin² A + cosec² A + 2}+{cos² A + sec² A + 2}

= 2 + 2 + (sin² A + cos² A) + sec² A + cosec² A

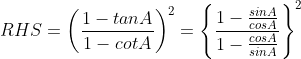
(1) और (2) से स्पष्ट है की

∴ LHS = RHS

अंत:,

इस पोस्ट में आपको NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.4 ,class 10 maths chapter 8 pdf ,class 10 Maths Chapter 8 Exercise 8.4 Introduction to Trigonometry Class 10 Maths chapter 8 exercise 8.4 question class 10 maths chapter 8 exercise 8.4 कक्षा 10 अध्याय 8. त्रिकोणमिति का परिचय प्रश्नावली 8.4 एनसीईआरटी समाधान कक्षा 10 गणित अध्याय 8 अभ्यास 8.4 त्रिकोणमिति का परिचय से संबंधित पूरी जानकारी दी गई है अगर इसके बारे में आपका कोई भी सवाल या सुझाव हो तो नीचे कमेंट करके हम से जरूर पूछें और अगर आपको यह जानकारी फायदेमंद लगे तो अपने दोस्तों के साथ शेयर जरूर करें.

NCERT Solutions for Class 10 Maths Chapter 8 त्रिकोणमिति का परिचय Exercise 8.1
NCERT Solutions for Class 10 Maths Chapter 8 त्रिकोणमिति का परिचय Exercise 8.2
NCERT Solutions for Class 10 Maths Chapter 8 त्रिकोणमिति का परिचय Exercise 8.3
NCERT Solutions for Class 10 Maths Chapter 8 त्रिकोणमिति का परिचय Exercise 8.4