Class 10 Maths Chapter 8 Exercise 8.1 – त्रिकोणमिति का परिचय

Class 10 Maths Chapter 8 Exercise 8.1 – त्रिकोणमिति का परिचय

NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.1 – हर विद्यार्थी का सपना होता है कि वे अपनी कक्षा में अच्छे अंक से पास हो ,ताकि उन्हें आगे एडमिशन या किसी नौकरी के लिए फॉर्म अप्लाई करने में कोई दिक्कत न आए . कक्षा 10वीं के विद्यार्थी के लिए यहां परएनसीईआरटी कक्षा 10 गणित अध्याय 8. (त्रिकोणमिति का परिचय) प्रश्नावली 8.1 के लिए सलूशन दिया गया है. जोकि एक सरल भाषा में दिया है .ताकि विद्यार्थी को पढने में कोई दिक्कत न आए .इसकी मदद से आप अपनी परीक्षा में अछे अंक प्राप्त कर सकते है.

NCERT Solutions For Class 10th Maths त्रिकोणमिति का परिचय (प्रश्नावली 8.1)

(i) sin A, cos A (ii) sin C, cos C

हल : दिया है,

AB = 24 cm, BC = 7 cm; ∠B = 90°

पाइथागोरस प्रमेय के प्रयोग से,

AC² = AB² + BC²

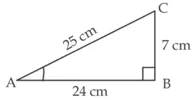
AC² = (24)² + (7)²
AC² = 576 + 49
AC² = 625
AC = √625
AC = 25 cm

(i)

अंत: और

(ii)

अंत: और

हल : कर्ण PR = 13 cm; PQ = 12 cm

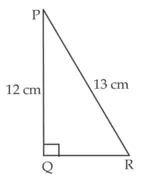
पाइथागोरस प्रमेय के प्रयोग से,

PR² = PQ² + QR²
या (13)² = (12)² + OR²
या 169 = 144 + (QR)²
या 169 – 144 = (QR)²
या 25 = (OR)²
या OR = ±√25
या OR = 5, – 5.
या QR = 5 cm.

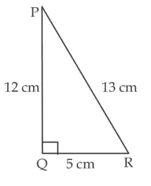
[∵ QR ≠ – 5, क्योंकि त्रिभुज की भुजा ऋणात्मक नहीं हो सकती]

∴

अंत: tan P – cot R = 0.

हल : मान लो, ∆ABC में, कोण B समकोण है

परंतु

∴

⇒ भुजा BC और AC का अनुपात 3 : 4 है
⇒ मान लो BC = 3k, AC = 4k, जहाँ k आनुपातिकता स्थिरांक है

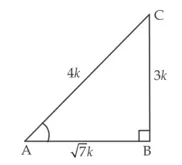
पाइथागोरस प्रमेय के प्रयोग से,
AC² = AB² + BC²
या (4k)² = (AB)² + (3k)²
या 16k² = AB² + 9k²
या 16k² – 9k² AB²
या 7k² = AB²

या

या

[∵ AB ≠ – √7k, क्योंकि भुजा ऋणात्मक नहीं हो सकती
⇒ AB = √7k

अंत: और

हल : मान लीजिए,

ABC कोई समकोण त्रिभुज है जिसमें A न्यून कोण है और B पर समकोण है।

15 cot A = 8.

परंतु

⇒

भुजा AB और BC का अनुपात 8 : 15 है
यदि AB = 8k, हो तो BC = 15 k, जहाँ k घनात्मक संख्या है

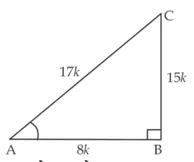
पाइथागोरस प्रमेय का प्रयोग करने पर,

AC² = (AB)² + (BC)²
(AC)² = (8k)² + (15 k)²
(AC)² = 64k² + 225 k²
(AC)² = 289 k²

AC = ± 17k

⇒ AC = 17k

[∵ AC = -17k, क्योंकि भुजा ऋणात्मक नहीं हो सकती]

अंत:, और

हल : मान लो समकोण त्रिभुज ABC में समकोण B पर है।

मान लो ∠BAC = 0

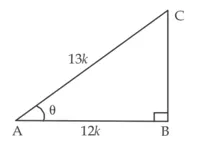
परंतु [आकृति से]

∴

⇒ यदि AC = 13k, हो तो AB = 12k,

जहाँ k घनात्मक संख्या है पाईथागोरस प्रमेय का प्रयोग करने पर

AC² = (AB)² + (BC)²
या (13k)² = (12k)² + (BC)²
या 169k² = 144k² + (BC)²
या 169k² – 144k² = (BC)²
या (BC)² = 25k²
या BC = ± √25 k²
या BC = ± 5k
या BC = 5k

[BC ≠ – 5k, क्योंकि भुजा ऋणात्मक नहीं हो सकती]

हल: मान लीजिए,

ABC कोई त्रिभुज है जहाँ ∠A और ∠B न्यून कोण है cos A और cos B ज्ञात करने है

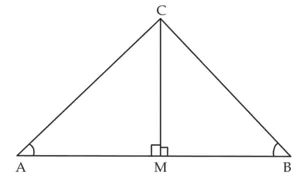
CM ⊥ AB
∠AMC = ∠BMC = 90
समकोण ∆AMC,

….(1)

समकोण ∆BMC,

….(2)

परंतु cos A = cos B [दिया है] ….(3)

(1),(2) और (3) से,

∴ ∆AMC ～ ∆BMC [SSS समरूपता से]⇒ ∠A = ∠B

[∵ क्योंकि समरूप त्रिभुजों के संगत कोण बराबर होते हैं]

प्रश्न 7. यदि तो का मान निकालिए।
हल: (i) ∠ABC = 0.

समकोण त्रिभुज ABC में C पर समकोण है

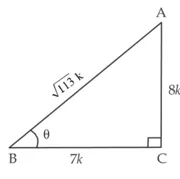
दिया है,

परंतु [आकृति से]

∴

यदि BC = 7k, हो तो AC = 8k ,

जहाँ k कोई भी धनात्मक संख्या है पाइथागोरस प्रमेय का प्रयोग करने से,

AB² = (BC)² + (AC)²
(AB)² = (7k)² + (8k)²
(AB)² = 49k² + 64k²
(AB)² = 113k²
AB = ± √113k²
AB = √113k²

[∵ AB ≠ – √113 K, क्योंकि भुजा ऋणात्मक नहीं हो सकती]

∴

∴

(1 + sin θ) (1 – sin θ)

[सूत्र (α + b) (α – b) = α² – b² के प्रयोग से]

….(1)

(1 + cos θ)(1 – cos θ)

[सूत्र (α + b) (α – b) = α² – b² के प्रयोग से]

….(2)

मान लो, =

[(1) और (2) से]

अत:,

(ii)

cot² θ = (cot θ)²

हल : मान लीजिए ABC एक समकोण त्रिभुज है जिसमें B पर समकोण है।

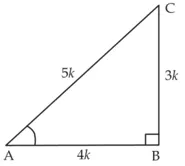
यह दिया है कि 3 cot A = 4

परंतु  [आकृति से]

⇒

⇒ यदि AB = 4k, हो तो BC = 3k,

जहाँ k धनात्मक संख्या है पाइथागोरस प्रमेय का प्रयोग करने पर,

(AC)² = (AB)² + (BC)²
(AC)² = (4k)² + (3k)²
(AC)² = 16k² + 9k²
(AC)² = 25k²

AC = ± 5k
परंतु AC = 5k

[AC ≠ – 5k, भुजा ऋणात्मक नहीं हो सकती]

=

= =

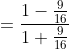
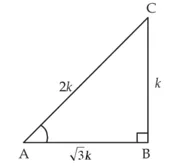
…..(1)

RHS = cos²A-sin²A

∴ …..(2)

(1) और (2) से

LHS = RHS

अंत:,

(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C.हल: (i) दिया है : ∆ABC जिसका कोण B समकोण है

….(1)

परंतु ….(2)

(1) और (2) से,

⇒ यदि BC = k, हो तो AB = √3 k
जहाँ k कोई भी धनात्मक संख्या है
समकोण त्रिभुज ABC में,

पाइथागोरस प्रमेय का प्रयोग करने पर,

(AC)² = (AB)² + (BC)²
(AC)² = (√3k)² + (k)²
AC² – 3k² + k²
AC² = 4k²
AC = ± √4k²
AC = ± 2k
AC = 2k

[∵ AC ≠ – 2k, ∵ भुजा ऋणात्मक नहीं हो सकती]

….(3)

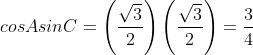
sin A cos C + cos A sin C

∴ sin A cos C + cos A sin C = 1

(ii) 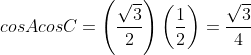[(3) से]

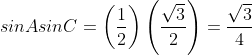[(3) से]

हल: दिया है ∆PQR में, समकोण Q पर है

PR + QR = 25cm
PQ = 5 cm
समकोण त्रिभुज PQR में

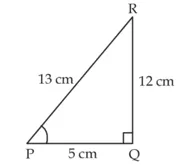
पाइथागोरस प्रमेय का प्रयोग करने पर,
(PR)² = (PQ)² + (RQ)²
या (PR)² = (5)² + (RO)²
[∵ PR + OR = 25] [QR = 25 – PR]

या (PR)² = 25 + [25 – PR]²
या (PR)² = 25 + (25)² + (PR)² – 2 x 25 x PR
या (PR)² = 25 + 625 + (PR)² – 50 PR
या (PR)² – (PR)² + 50 PR = 650
या 50 PR = 650

या

या PR = 13 cm
QR = 25 – PR
⇒ QR = (25 – 13) cm
या OR = 12 cm.

(i) tan A का मान सदैव 1 से कम होता है।
(ii) कोण A के किसी मान के लिए
(iii) cos A कोण A के लिए प्रयुक्त एक संक्षिप्त रूप है।
(iv) cot A और A का गुणनफल होता है।
(v) किसी भी कोण के लिए

हल : (i) असत्य

∵ tan 60° = √3 = 1.732 1.

(ii) सत्य 1. (सत्य)
::: sec A सदैव 1 से बड़ा होता है।

(iii) असत्य
क्योंकि cos A, cosine A के लिए प्रयोग किया जाता है।

(iv) असत्य
क्योंकि cot A कोण A का contangent है cot और A का गुणफल नहीं है।

(v) असत्य 1

क्योंकि sin θ सदैव 1 से कम होता है।

इस पोस्ट में आपको NCERT Solutions for Class 10 Maths Exercise 8.1 ,Class 10 Maths Chapter 8 Introduction to Trigonometry ,class 10 maths chapter 8 exercise 8.1 solutions Class 10 Maths Exercise 8.1 Chapter 8 – Introduction to Trigonometry एनसीईआरटी समाधान कक्षा 10 गणित प्रश्नावली 8.1 एनसीईआरटी कक्षा-10 प्रश्नावली 8.1 त्रिकोणमिति का परिचय से संबंधित पूरी जानकारी दी गई है अगर इसके बारे में आपका कोई भी सवाल या सुझाव हो तो नीचे कमेंट करके हम से जरूर पूछें और अगर आपको यह जानकारी फायदेमंद लगे तो अपने दोस्तों के साथ शेयर जरूर करें.

NCERT Solutions for Class 10 Maths Chapter 8 त्रिकोणमिति का परिचय Exercise 8.1
NCERT Solutions for Class 10 Maths Chapter 8 त्रिकोणमिति का परिचय Exercise 8.2
NCERT Solutions for Class 10 Maths Chapter 8 त्रिकोणमिति का परिचय Exercise 8.3
NCERT Solutions for Class 10 Maths Chapter 8 त्रिकोणमिति का परिचय Exercise 8.4