Class 10 Maths Chapter 14 Exercise 14.3 – सांख्यिकी
NCERT Solutions for Class 10 Maths Chapter 14 Statistics Ex 14.3 – हर विद्यार्थी का सपना होता है कि वे अपनी कक्षा में अच्छे अंक से पास हो ,ताकि उन्हें आगे एडमिशन या किसी नौकरी के लिए फॉर्म अप्लाई करने में कोई दिक्कत न आए . कक्षा 10वीं के विद्यार्थी के लिए यहां परएनसीईआरटी कक्षा 10 गणित अध्याय 14. (सांख्यिकी) प्रश्नावली 14.3 के लिए सलूशन दिया गया है. जोकि एक सरल भाषा में दिया है .ताकि विद्यार्थी को पढने में कोई दिक्कत न आए .इसकी मदद से आप अपनी परीक्षा में अछे अंक प्राप्त कर सकते है.
NCERT Solutions For Class 10th Maths सांख्यिकी (प्रश्नावली 14.3)
| मासिक खपत (इकाइयों में) | उपभोक्ताओं की संख्या |
| 65-85 85-105 105-125 125-145 145-165 165-185 185-205 | 4 5 13 20 14 8 4 |
माध्यक के लिए :
| मासिक खपत (इकाइयों में) | उपभोक्ताओं की संख्या (fi) | संचयी बारंबारता |
| 65-85 85-105 105-125 125-145 145-165 165-185 185-205 | 4 5 13 20 14 8 4 | 4 9 22 42 56 64 68 |
| योग | ∑fi = n = 68 |
यहाँ, ∑fi n = 68 तो 
जो कि वर्ग-अंतराल 125 – 145 में स्थित है।
∴ माध्यक वर्ग = 125 – 145
अतः, l = 125; n = 68; f = 20; cf = 22 और h = 20
सूत्र का प्रयोग करने पर,
माध्यक 
= 125 + 12 = 137
माध्य के लिए :
| मासिक खपत (इकाइयों में) | उपभोक्ताओं की संख्या (fi) | वर्ग चिन्ह (????i) |  या  | fiui |
| 65-85 85-105 105-125 125-145 145-165 165-185 185-205 | 4 5 13 20 14 8 4 | 75 95 115 135 155 175 195 | -3 -2 -1 0 1 2 3 | 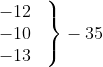 0  |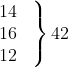
| योग | ∑fi = n = 68 | ∑fiui = 7 |
उपरोक्त आंकड़ों से,
कल्पित मान (α) = 135
वर्ग-माप (h) = 20
∴ 
सूत्र का प्रयोग करने पर,
माध्य 
x = 135 + 20 (0.102)
135 + 2.04 = 137.04
बहुलक के लिए :
दिए गए आंकड़ों में, अधिकतम बारंबारता 20 है और इसके संगत-वर्ग 125 – 145 है।
∴ बहुलक वर्ग = 125 – 145
इसलिए, 1 = 125; f1 = 20; f0 = 13; f2 = 14 और h = 20
सूत्र का प्रयोग करने पर,
बहुलक 
बहुलक 
= 125 + 10.76923
= 125 + 10.77
= 135.77
अतः, दिए गए आंकड़ों का माध्यक, माध्य और बहुलक है : 137 मात्रक, 137.04 मात्रक और 135.77 मात्रक।
| वर्ग-अंतराल | बारंबारता |
| 0-10 10-20 20-30 30-40 40-50 50-60 | 5 x 20 15 y 5 |
| योग | 60 |
| वर्ग-अंतराल | बारंबारता (fi) | संचयी बारंबारता (cf) |
| 0-10 10-20 20-30 30-40 40-50 50-60 | 5 x 20 15 y 5 | 5 5 + x 25 + x 40 + x 40 + x + y 45 + x + y |
| योग | ∑fi = n = 60 |
दिए गए आंकड़ों में, ∑fi = n = 60
∴ 
साथी ही, बंटन का माध्यक = 28.5 (दिया है)
जो कि वर्ग-अंतराल 20-30 में स्थित है।
∴ माध्यक वर्ग = 20 – 30
इसलिए, l = 20; f = 20; cf = 5 + x; h = 10
सारणी से यह स्पष्ट है कि 45 + x + y = 60
या x + y = 60 – 45 = 15
या x + y = 15 …(1)
अब, सूत्र का प्रयोग करने पर, माध्यक 
या 
या 
या 2(28.5) = 65 – x
या 57.0 = 65 – x
या x = 65 – 57 = 8
∴ x = 8
x के इस मान को (1) में प्रतिस्थापित करने पर, हमें प्राप्त होता है।
8 + y = 15
y = 15 – 8 = 7
अतः, x और y के मान 8 और 7 हैं।
| आयु (वर्षों में) | पॉलिसी धारकों की संख्या |
| 20 से कम 25 से कम 30 से कम 35 से कम 40 से कम 45 से कम 50 से कम 55 से कम 60 से कम | 2 6 24 45 78 89 92 98 100 |
| आयु (वर्षों में) | संचयी बारंबारता | पॉलिसी धारकों की संख्या (fi) |
| 20 से कम 20-25 25-30 30-35 35-40 40-45 45-50 50-55 55-60 | 2 6 24 45 78 89 92 98 100 | 2 6 – 2 = 4 24 – 6 = 18 45 – 24 = 21 78 – 45 = 33 89 – 78 = 11 92 – 89 = 3 98 – 92 = 6 100 – 98 = 2 |
| योग | ∑fi = n = 100 |
यहाँ, ∑fi = n = 100
तो, 
जोकि अंतराल 35 – 40 में स्थित है।
∴ माध्यक वर्ग = 35 – 40
इसलिए, l = 35; n = 100; f = 33; cf = 45 और h = 5
सूत्र का प्रयोग करने पर,माध्यक
= 35 + 0.76 (लगभग) = 35.76
अतः, दिए गए आंकड़ों की माध्यक आयु 35.76 वर्ष है।
| लंबाई (mm में) | परिवारों की संख्या |
| 118-126 127-135 136-144 145-153 154-162 163-171 172-180 | 3 5 9 12 5 4 2 |
क्योंकि, बारंबारता बंटन लगातार नहीं है हम इसे पहले लगातार बंटन में परिवर्तित करेंगे :
| लम्बाई (mm में) | पत्तियों की संख्या (fi) | संचयी बारंबारता (cf) |
| 117.5-126.5 126.5-135.5 135.5-144.5 144.5-153.5 153.5-162.5 162.5-171.5 171.5-180.5 | 3 5 9 12 5 4 2 | 3 (3 + 5) = 8 (8 + 9) = 17 (17 + 12) = 29 (29 + 5) = 34 (34 + 4) = 38 (38 + 2) = 40 |
| योग | ∑fi = n = 40 |
यहाँ, ∑fi = n = 40
तो, 
जो कि अंतराल 144.5 – 153.5 में स्थित है।
∴ माध्यक वर्ग = 144.5 – 153.5
इसलिए, l = 144.5; f = 12; cf = 17; h = 9
सूत्र का प्रयोग करने पर, माध्यक
माध्यक 
= 144.5 + 2.25 = 146.7
अतः पत्तियों की माध्यक लम्बाई 146.75 mm है।
| जीवन-काल (घंटों में) | लैंपों की संख्या |
| 1500-2000 2000-2500 2500-3000 3000-3500 3500-4000 4000-4500 4500-5000 | 14 56 60 86 74 62 48 |
एक लैंप का माध्यक जीवनकाल ज्ञात कीजिए।
हल :
| जीवनकाल (घंटों में) | लैंपों की संख्या (fi) | संचयी बारंबारता (cf) |
| 1500-2000 2000-2500 2500-3000 3000-3500 3500-4000 4000-4500 4500-5000 | 14 56 60 86 74 62 48 | 14 (14 + 56) = 70 (70 + 60) = 130 (130 + 86) = 216 (216 + 74) = 290 (290 + 62) = 352 (352 + 48) = 400 |
| योग | ∑fi = n = 400 |
यहाँ, ∑fi = n = 400
∴ 
जोकि अंतराल 3000 – 3500 में स्थित है।
∴ माध्यक वर्ग = 3000 – 3500
इसलिए, l = 3000; n = 400 ; f = 86 ; cf = 130 और h = 500
सूत्र का प्रयोग करने पर,माध्यक
माध्यक 
= 3000 + 406.9767441
= 3000 + 406.98 (लगभग)
= 3406.98
अतः, लैंप का जीवनकाल 3406.98 घंटे है।
| अक्षरों की संख्या | 1-4 | 4-7 | 7-10 | 10-13 | 13-16 | 16-19 |
| कुल नामों की संख्या | 6 | 30 | 40 | 16 | 4 | 4 |
कुल नामों में माध्यक अक्षरों की संख्या ज्ञात कीजिए। कुल नामों में माध्य अक्षरों की संख्या ज्ञात कीजिए। साथ ही, कुल नामों का बहुलक ज्ञात कीजिए।
हल : माध्यक के लिए :
| अक्षरों की संख्या | कुल नामों की संख्या (fi) | संचयी बारंबारता |
| 1-4 4-7 7-10 10-13 13-16 16-19 | 6 30 40 16 4 4 | 6 = 6 6 + 30 = 36 36 + 40 = 76 76 + 16 = 92 92 + 4 = 96 92 + 4 = 100 |
| योग | ∑fi = n = 100 |
यहाँ, ∑fi = n = 100
∴ 
जो कि अंतराल 7-10 में स्थित है।
∴ माध्यक वर्ग = 7 – 10
इसलिए, l = 7; n = 100; f = 40 ; cf = 36 और h = 3
सूत्र का प्रयोग करने पर,माध्यक
माध्यक 
= 7 + 1.05 = 8.05
अतः, माध्यक अक्षरों की संख्या 8.05 है।
माध्य के लिए :
| अक्षरा का संख्या | fi | वर्ग चिन्ह (????i) | या  | fiui |
| 1-4 4-7 7-10 10-13 13-16 16-19 | 6 30 40 16 4 4 | 2.5 5.5 8.5 = α 11.5 14.5 17.5 | -2 -1 0 1 2 3 |  0  |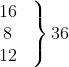
| योग | ∑fi = 100 | ∑fiui = – 6 |
उपरोक्त आंकड़ों से,
कल्पित माध्य (α) = 8.5
वर्ग माप (h) = 3
∴ 
सूत्र का प्रयोग करने पर,माध्य 
x = 8.5 + 3 (- 0.06)
= 8.5 – 0.18
= 8.32
अतः, कुल नामों में माध्य अक्षरों की संख्या 8.32 अक्षर है।
बहुलक के लिए :
दिए गए आंकड़ों में, अधिकतम बारंबारता 40 है और इसका संगत अंतराल 7 – 10 है।
∴ बहुलक वर्ग = 7 – 10
इसलिए, l = 7; f1 = 40; f0 = 30; f2 = 16 और h = 3
सूत्र का प्रयोग करने पर, 
बहुलक 
= 7 + 0.88 (लगभग)
= 7.88
अतः, कुल नामों का बहुलक 7.88 अक्षर है।
| भार (किलोग्राम में) | 40-45 | 45-50 | 50-55 | 55-60 | 60-65 | 65-70 | 70-75 |
| विद्यार्थियों की संख्या | 2 | 3 | 8 | 6 | 6 | 3 | 2 |
| भार (किलोग्राम में) | विद्यार्थियों की संख्या (fi) | संचयी बारंबारता (cf) |
| 40-45 45-50 50-55 55-60 60-65 65-70 70-75 | 2 3 8 6 6 3 2 | 2 = 2 2 + 3 = 5 5 + 8 = 13 13 + 6 = 19 19 + 6 = 25 25 + 3 = 28 28 + 2 = 30 |
| योग | ∑fi = n = 30 |
यहाँ, ∑fi = n = 30
∴ 
जोकि अंतराल 55 – 60 में स्थित है।
∴ माध्यक वर्ग = 55 – 60
इसलिए, l = 55; n = 30; f = 6; cf = 13 और h = 5
सूत्र का प्रयोग करने पर, माध्यक
माध्यक 
= 55 + 1.66666
= 55 + 1.67 (लगभग) = 56.67
अतः, विद्यार्थियों का माध्यक भाग 56.67 किलोग्राम है।
इस पोस्ट में आपको Class 10 Maths Chapter 14 Exercise 14.3 Statistics Class 10 Maths Chapter 14 Exercise 14.3 Class 10 Maths Chapter 14 Statistics NCERT Solutions Class 10 Maths Chapter 14 Exercise 14.3 class 10 maths chapter 14 pdf solutions statistics class 10 pdf notes Class 10 Maths Exercise 14.3 NCERT solutions in Hindi कक्षा 10 गणित अध्याय 14 अभ्यास 14.3 सांख्यिकी Class 10 Maths Solutions Chapter 14 सांख्यिकी Ex 14.3 कक्षा 10 गणित अध्याय 14 अभ्यास 14.3 सांख्यिकी से संबंधित पूरी जानकारी दी गई है अगर इसके बारे में आपका कोई भी सवाल या सुझाव हो तो नीचे कमेंट करके हम से जरूर पूछें और अगर आपको यह जानकारी फायदेमंद लगे तो अपने दोस्तों के साथ शेयर जरूर करें.
NCERT Solutions for Class 10 Maths Chapter 14 सांख्यिकी Exercise 14.1
NCERT Solutions for Class 10 Maths Chapter 14 सांख्यिकी Exercise 14.2
NCERT Solutions for Class 10 Maths Chapter 14 सांख्यिकी Exercise 14.3
NCERT Solutions for Class 10 Maths Chapter 14 सांख्यिकी Exercise 14.4