Class 10 Maths Chapter 14 Exercise 14.2 – सांख्यिकी
NCERT Solutions for Class 10 Maths Chapter 14 Statistics Ex 14.2 – जो विद्यार्थी 10वीं कक्षा में पढ़ रहे है उनके लिए यहां पर एनसीईआरटी कक्षा 10 गणित अध्याय 14. (सांख्यिकी) प्रश्नावली 14.2 के लिए सलूशन दिया गया है. जोकि एक सरल भाषा में दिया है .ताकि विद्यार्थी को पढने में कोई दिक्कत न आए .इसकी मदद से आप अपनी परीक्षा में अछे अंक प्राप्त कर सकते है. इसलिए निचे आपको एनसीईआरटी समाधान कक्षा 10 गणित अध्याय 14 सांख्यिकी प्रश्नावली 14.2 दिया गया है .
NCERT Solutions For Class 10th Maths सांख्यिकी (प्रश्नावली 14.2)
| आयु वर्षों में | 5 – 15 | 15 – 25 | 25 – 35 | 35 – 45 | 45 – 55 | 55 – 65 |
| रोगियों कि संख्या | 6 | 11 | 21 | 23 | 14 | 5 |
उपरोक्त आँकड़ों के बहुलक और माध्य ज्ञात कीजिए | दोनों केन्द्रीय प्रवृत्ति कि मापों की तुलना कीजिए और उनकी व्याख्या कीजिए |
हल : बहुलक के लिए : दिए गए आंकड़ों में अधिकतम बारंबारता 23 है और इसके संगत वर्ग-अंतराल 35 – 45 है:
∴ बहुलक वर्ग = 35 – 45
इसलिए, l = 35; f1 = 23; f0 = 21; f2 = 14 और h = 10 सूत्र का प्रयोग करने पर,
बहुलक ![]()
बहुलक ![]()
बहुलक ![]()
![]()
माध्य के लिए:
| आयु (वर्षों में) | रोगियों की संख्या (fi) | वर्ग चिन्ह (????i) | या | fiui |
| 5-15 15-25 25-35 35-45 45-55 55-65 | 6 11 21 23 14 5 | 10 20 30 40 50 60 | -2 -1 0 1 2 3 | 0  |
| योग | ∑fi = 80 | ∑fiui = 43 |
उपरोक्त आंकड़ों से,
कल्पित मान (α) = 30
वर्ग माप (h) = 10
∴ ![]()
सूत्र का प्रयोग करने पर, माध्य ![]()
x = 30 + 10 (0.5375)
= 30 + 5.375
= 35.375 = 35.37
अतः, दिए गए आंकड़ों का बहुलक 36.8 वर्ष है और दिए गए आँकड़ों का माध्य 35.37 है।
साथ ही, उपरोक्त चर्चा से यह स्पष्ट है कि अस्पताल में भर्ती हुए रोगियों की औसत आयु 35.37 वर्ष है और अस्पताल में भर्ती हुए अधिकतम रोगियों की आयु 36.8 वर्ष है।
| जीवन काल (घंटों में) | 0-20 | 20-40 | 40-60 | 60-80 | 80-100 | 100-120 |
| बारंबारता | 10 | 35 | 52 | 61 | 38 | 29 |
उपकरणों का बहुलक जीवन-काल ज्ञात कीजिए।
हल : दिए गए आंकड़ों में,
अधिकतम बारंबारता 61 है और इसकी संगत वर्ग अंतराल 60 – 80 है।
∴ बहुलक वर्ग = 60 – 80
अतः, l = 60.; f1h = 61; f0 = 52 ; f2 = 38 और h = 20
सूत्र का प्रयोग करने पर,
बहुलक ![]()
![]()
![]()
![]()
![]()
= 60 + 5.625 = 65.625
अत: उपकरणों का बहुलक जीवन-काल 65.625 घंटे है।
| व्यय ( ₹ में) | परिवारों की संख्या |
| 1000-1500 1500-2000 2000-2500 2500-3000 3000-3500 3500-4000 4000-4500 4500-5000 | 24 40 33 28 30 22 16 7 |
बहुलक के लिए : दिए गए आंकड़ों में अधिकतम बारंबारता 40 है तथा इस बारंबारता के संगत वर्ग 1500 – 2000 हैं।
∴ बहुलक वर्ग = 1500 – 2000
अतः, l = 1500 ; f1 = 40 ; f0 = 24 ; f2 = 33 और h = 500
सूत्र का प्रयोग करने पर,
बहुलक ![]()
![]()
![]()
![]()
![]()
= 1500 + 347.83 =1847.83
माध्य के लिए :
| व्यय (₹ में) | परिवारों की संख्या (fi) | वर्ग चिन्ह (????i) | या | fiui |
| 1000-1500 1500-2000 2000-2500 2500-3000 3000-3500 3500-4000 4000-4500 4500-5000 | 24 40 33 28 30 22 16 7 | 1250 1750 2250 2750 3250 3750 4250 4750 | -3 -2 -1 0 1 2 3 4 | 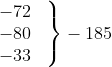 0 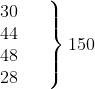 |
| योग | ∑fi = 200 | ∑fiui = – 35 |
उपरोक्त आंकड़ों से,
कल्पित माध्य (α) = 2750
वर्ग माप (h) = 500
∴ ![]()
![]()
सूत्र का प्रयोग करने पर,
माध्य ![]()
x = 2750 + 500 (- 0.175)
= 2750 – 87.50
= 2662.50
अतः, परिवारों का बहुलक मासिक व्यय ₹ 1847.83 है और माध्य मासिक व्यय ₹ 2662.50 है।
| प्रतिशिक्षक विद्यार्थियों की संख्या | 15-20 | 20-25 | 25-30 | 30-35 | 35-40 | 40-45 | 45-50 | 50-55 |
| राज्य/संघीय क्षेत्रों की संख्या | 3 | 8 | 9 | 10 | 3 | 0 | 0 | 2 |
दिए गए आंकड़ों में,
अधिकतम बारंबारता 10 है और इसके संगत वर्ग अंतराल 30-35 है।
∴ बहुलक वर्ग = 30 – 35.
इसलिए, l = 30; f1 = 10; f0 = 9; f2 = 3 और h = 5
सूत्र का प्रयोग करने पर,बहलक ![]()
![]()
![]()
![]()
= 30 + 0.625
= 30.625 = 30.63 (लगभग)
माध्य के लिए :
| प्रतिशिक्षक विद्यार्थियों की संख्या | राज्य/संघीय क्षेत्रों की संख्या (fi) | वर्ग चिन्ह (????i) | fiui | |
| 15-20 20-25 25-30 30-35 35-40 40-45 45-50 50-55 | 3 8 9 10 3 0 0 2 | 17.5 22.5 27.5 32.5 37.5 42.5 47.5 52.5 | -3 -2 -1 0 1 2 3 4 | 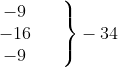 0 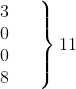 |
| योग | ∑fi = 35 | ∑fiui = – 23 |
उपरोक्त आंकड़ों से,
कल्पित माध्य (α) = 32.5
वर्ग माप (h) = 5
∴ ![]()
माध्य ![]()
x = 32.5 + 5 (- 0.65)
= 32.5 – 3.25 = 29.25 (लगभग)
अतः दिए गए आंकड़ों का बहुलक और माध्य 30.63 और 29.25 है। साथ ही, उपरोक्त चर्चा से यह स्पष्ट है कि राज्यों/संघीय क्षेत्रों में प्रतिशिक्षक विद्यार्थियों की संख्या 30.63 है और औसत के अनुसार यह अनुपात 29.25 है।
| बनाए गए रन | बल्लेबाजों की संख्या |
| 3000-4000 4000-5000 5000-6000 6000-7000 7000-8000 8000-9000 9000-10000 10000-11000 | 4 18 9 7 6 3 1 1 |
इन आंकड़ों का बहुलक ज्ञात कीजिए।
हल : दिए गए आंकड़ों में,
अधिकतम बारंबारता 18 है और इसके संगत वर्ग अंतराल 4000 – 5000 है।
∴ बहुलक वर्ग = 4000 – 5000
अतः l = 4000; f1 = 18; f0 = 4; f2 = 9 और h = 1000
सूत्र का प्रयोग करने पर,
बहुलक ![]()
![]()
![]()
![]()
= 4000 + 608.7 = 4608.7 (लगभग)
अतः, दिए गए आंकड़ों का बहुलक 4608.7 रन है।
| कारों की संख्या | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 |
| बारंबारता | 7 | 14 | 13 | 12 | 20 | 11 | 15 | 8 |
दिए गए आंकड़ों में,
अधिकतम बारंबारता 20 है और इसके संगत वर्ग अंतराल 40-50 हैं।
∴ बहुलक वर्ग = 40-50
इसलिए, l = 40; f1 = 20; f0 = 12; f2 = 11 और h = 10
सूत्र का प्रयोग करने पर,बहुलक ![]()
![]()
![]()
![]()
= 40 + 4.7 = 44.7 (लगभग)
अतः, दिए हुए आंकड़ों का बहुलक 44.7 कारें हैं।
इस पोस्ट में आपको Class 10 maths chapter 14 exercise 14.2 statistics Class 10 Exercise 14.2 Solutions Class 10 maths chapter 14 notes pdf download class 10 statistics solutions NCERT Solutions for Class 10 Maths Chapter 14 – Statistics Class 10 Maths Chapter 14 exercise 14.2 Question एनसीईआरटी समाधान कक्षा 10 गणित अध्याय 14 अभ्यास 14.2 सांख्यिकी कक्षा 10 गणित अध्याय 14 सांख्यिकी (प्रश्नावली 14.2) Class 10 गणित सांख्यिकी प्रश्नावली 14.2 से संबंधित पूरी जानकारी दी गई है अगर इसके बारे में आपका कोई भी सवाल या सुझाव हो तो नीचे कमेंट करके हम से जरूर पूछें और अगर आपको यह जानकारी फायदेमंद लगे तो अपने दोस्तों के साथ शेयर जरूर करें.
NCERT Solutions for Class 10 Maths Chapter 14 सांख्यिकी Exercise 14.1
NCERT Solutions for Class 10 Maths Chapter 14 सांख्यिकी Exercise 14.2
NCERT Solutions for Class 10 Maths Chapter 14 सांख्यिकी Exercise 14.3
NCERT Solutions for Class 10 Maths Chapter 14 सांख्यिकी Exercise 14.4