Class 10 Maths Chapter 13 Exercise 13.5 – पृष्ठीय क्षेत्रफल और आयतन

NCERT Solutions for Class 10 Maths Chapter 13 Surface Areas And Volumes Ex 13.5 – आज हम आप के लिए Class 10 Maths Chapter 13 लेकर आयें है। जो कि Class 10 Maths Exams के लिए अत्यन्त उपयोगी साबित होगी. कक्षा 10वीं के विद्यार्थी के लिए यहां पर एनसीईआरटी कक्षा 10 गणित अध्याय 13. (पृष्ठीय क्षेत्रफल और आयतन) प्रश्नावली 13.5 के लिए सलूशन दिया गया है. जोकि एक सरल भाषा में दिया है .ताकि विद्यार्थी को पढने में कोई दिक्कत न आए .इसकी मदद से आप अपनी परीक्षा में अछे अंक प्राप्त कर सकते है.

NCERT Solutions For Class 10th Maths पृष्ठीय क्षेत्रफल और आयतन (प्रश्नावली 13.5)

1. व्यास 3 mm वाले ताँबे के तार को 12 cm लंबे और 10 cm व्यास वाले एक बेलन पर इस प्रकार लपेटा जाता है कि वह बेलन के वक्र पृष्ठ को पूर्णतया ढक लेता है। तार की लंबाई और द्रव्यमान ज्ञात कीजिए, यह मानते हुए कि ताँबे का घनत्व 8.88 g प्रति cm है।

हल : तार का व्यास (d) = 3 mm

∴ तार की त्रिज्या

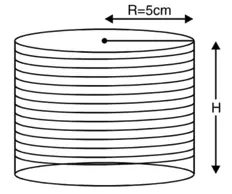
बेलन का व्यास= 10 cm
बेलन की त्रिज्या (R) = 5 cm
बेलन की ऊँचाई (H) = 12 cm

बेलन का परिमाप = एक लपेटे में प्रयुक्त तार की लंबाई

2????R = एक लपेटे में प्रयुक्त तार की लंबाई

एक लपेटे में प्रयुक्त तार की लंबाई

लपेटों की संख्या = बेलन की ऊँचाई/तार का व्यास

∴ प्रयुक्त तार की लंबाई = लपेटों की संख्या

x एक लपेटे में प्रयुक्त तार की लंबाई

= 1257.14 cm

प्रयुक्त तार का आयतन = ????r²H

= 88.89 cm³

1 cm³ का द्रव्यमान = 8.88 g
88.89 cm³ का द्रव्यमान = 8.88 x 88.89 g
= 789.41 g

2. एक समकोण त्रिभुज, जिसकी भुजाएँ 3 cm और 4 cm हैं (कर्ण के अतिरिक्त), को उसके कर्ण के परितः घुमाया जाता है। इस प्रकार प्राप्त द्वि-शंकु (double cone) के आयतन और पृष्ठीय क्षेत्रफल ज्ञात कीजिए। (???? का मान जो भी उपयुक्त लगे, प्रयोग कीजिए।)

हल : मान लीजिए ∆ABC समकोण त्रिभुज हैं जिसके A पर समकोण है। AB और AC का माप क्रमशः 3 cm और 4 cm है।

भुजा BC (कर्ण) की लंबाई यहां, AO (या A’O) प्राप्त द्विशंकु के साझें आधार की त्रिज्या है, जोकि समकोण त्रिभुज के भुजा BC के परितः घूमने से बनती है।

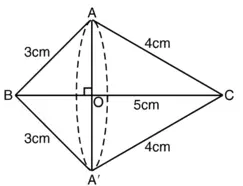
शंकु BAA’ की ऊँचाई BO और तिर्यक ऊँचाई 3 cm है।
शंकु CAA’ की ऊँचाई CO और तिर्यक ऊँचाई 4 cm है।
अब, ∆AOB ~ ∆CAB (AA समरुपता)

∴

⇒

साथ ही

⇒

अतः CO = BC – OB

अब द्विशंकु का आयतन = शंकु ABA’ का आयतनन + शंकु ACA’ का आयतन

∴ द्विशंकु का आयतन

अब द्विशंकु का पृष्ठीय क्षेत्रफल

= [शंकु ABA’ का पृष्ठीय क्षेत्रफल] + [शंकु ACA’ का पृष्ठीय क्षेत्रफल

= ????.AO . AB + ????.AO.A’C

= ????.AO . [AB + AC]

3. एक टंकी, जिसके आंतरिक मापन 150 cm x 120 cm x 110 cm हैं, में 129600 cm³ पानी है। इस पानी में कुछ छिद्र वाली ईंटें तब तक डाली जाती हैं, जब तक कि टंकी पूरी ऊपर तक भर न जाए। प्रत्येक ईंट अपने आयतन का

वां भाग पानी सोख लेती है। यदि प्रत्येक ईंट का माप 22.5 cm x 7.5 cm x 6.5 cm हैं, तो टंकी में कुल कितनी ईंटें डाली जा सकती हैं, ताकि उसमें से पानी बाहर न बहे ?

हल : एक ईंट का आयतन = 22.5 x 7.5 x 6.5 cm³
= 1096.87 cm³
टंकी का आयतन = 150 x 120 x 110 cm³
= 1980000 cm³
मान लीजिए प्रयुक्त ईंटों की संख्या = n
टंकी में ईंटों के लिए उपलब्ध आयतन
= 1980000 cm³ – 129600 cm³
= 1850400 cm³

प्रत्येक ईंट अपने आयतन का वाँ भाग पानी अवशोषित करती है।

टंकी में एक ईंट डालने से पानी के आयतन में वृद्धि

एक ईंट का आयतन

= 1032.35 cm³

n = 1792.42

प्रयुक्त ईंटों की संख्या = 1792 उत्तर

4. किसी महीने के 15 दिनों में, एक नदी की घाटी में 10 cm वर्षा हुई। यदि इस घाटी का क्षेत्रफल 97280 km² है, तो दर्शाइए कि कुल वर्षा लगभग तीन नदियों के सामान्य पानी के योग के समतुल्य थी, जबकि प्रत्येक नदी 1072 km लंबी, 75 m चौड़ी और 3 m गहरी है।

हल : घाटी का क्षेत्रफल = 97280 km²
घाटी में वर्षा = 10 cm

∴ कुल वर्षा का आयतन
= 9.728 km³ उत्तर

एक नदी में पानी का आयतन

= 1072 km x 75 m x 3m

तीन नदियों में पानी के आयतन

= 7.23 km³
यह वर्ष के पानी के आयतन के समतुल्य है।

5. टीन की बनी हुई एक तेल की कुप्पी 10 cm लंबे एक बेलन में एक शंकु के छिन्नक को जोड़ने से बनी है। यदि इसकी कुल ऊँचाई 22 cm है, बेलनाकार भाग का व्यास 8 cm है और कुप्पी के ऊपरी सिरे का व्यास 18 cm है, तो इसके बनाने में लगी टीन की चादर का क्षेत्रफल ज्ञात कीजिए। (देखिए आकृति)

हल : कुप्पी के ऊपरी सिरे का व्यास = 18 cm

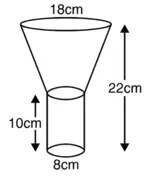
∴ कुप्पी के ऊपरी सिरे की त्रिज्या

= 9 cm

कुप्पी के आधार का व्यास = 8 cm
कुप्पी के आधार की त्रिज्या (r) = 4 cm
बेलनाकार भाग की ऊँचाई (h) = 10 cm
छिन्नक की ऊँचाई (H) = (22 – 10) cm
= 12 cm

छिन्नक की तिर्यक ऊँचाई (l)

छिन्नक की तिर्यक ऊँचाई (l) = 13 cm

टीन की चादर का क्षेत्रफल = बेलनाकार भाग का वक्र पृष्ठीय क्षेत्रफल +
छिन्नक का वक्र पृष्ठीय क्षेत्रफल

= 2????rh + ????L [R + r]

= (251.42 + 531.14) cm² = 782.56 cm²

प्रयुक्त की गई धातु की चादर का कुल क्षेत्रफल
= 782.56 cm² उत्तर

6. शंकु के छिन्नक के लिए, पूर्व स्पष्ट किए संकेतों का प्रयोग करते हुए, वक्र पृष्ठीय क्षेत्रफल और संपूर्ण पृष्ठीय क्षेत्रफल के उन सूत्रों को सिद्ध कीजिए, जो अनुच्छेद 13.5 में दिये गए हैं।

हल : एक लंब वृत्तीय शंकु के छिन्नक के दो असमान वृत्ताकार आधार और वक्र पृष्ठ होता है। मान लीजिए भाग VCD को हटाकर प्राप्त छिन्नक ACDB है। दोनों आधारों के केन्द्रों को मिलाने वाला रेखाखंड OP, छिन्नक की ऊँचाई कहलाता है। छिन्नक ACDB का प्रत्येक रेखाखंड AC और BD तिर्यक ऊँचाई है।

मान लीजिए R और r (R > r) शंकु (VAB) के छिन्नक ACDB के वृत्तीय सिरों की त्रिज्याएँ हैं। हम शंक्वाकार भाग VCD को पूरा करते हैं। मान लीजिए h और l क्रमशः ऊर्ध्वाधर ऊँचाई और तिर्यक ऊँचाई है। तब OP = h और AC = BD = l.
लंब वृत्तीय शंकु के छिन्नक को दो लंबवृत्तीय शंकुओं के बराबर VAB और VCD के अंतर के रूप में देखा जा सकता है।
मान लीजिए शंकु VAB की ऊँचाई h₁ और तिर्यक ऊँचाई l₁ है। अर्थात् VP = h₁ और VA = VB = l₁.

अब समकोण त्रिभुज ∆DEB में,

DB² = DE² + BE²

⇒ l² = h² + (R – r)²

⇒

पुनः ∆VOD ~ ∆VPB

⇒

अब

शंकु के छिन्नक का वक्र पृष्ठीय क्षेत्रफल

= ????Rl₁ – ????r(l₁ – l)

[शंकु का वक्र पृष्ठीय क्षेत्रफल = ???? x r x l]

= ????l(R + r) वर्ग मात्रक

∴ लंब वृत्तीय शंकु की छिन्नक का वक्र पृष्ठीय क्षेत्रफल

= ????l(R + r) वर्ग मात्रक

जहाँ

और लंब वृत्तीय शंकु की छिन्नक का कुल पृष्ठीय क्षेत्रफल

= वक्र पृष्ठीय क्षेत्रफल + आधार का क्षेत्रफल + ऊपरी सिरे का क्षेत्रफल

= ????l (R + r) + ????R² + ????²
= ????[R² + r² + 1 (R + r)] वर्ग मात्रक। उत्तर

7. शंकु के एक छिन्नक के लिए, पूर्व स्पष्ट किए संकेतों का प्रयोग करते हुए, आयतन का वह सूत्र सिद्ध कीजिए, जो अनुच्छेद 13.5 में दिया गया है।

मान लीजिए R और r (R > r) शंकु (VAB) के छिन्नक ACDB के वृत्तीय सिरों की त्रिज्याएँ हैं। हम शंक्वाकार भाग VCD को पूरा करते हैं।

मान लीजिए h और ] क्रमश: ऊर्ध्वाधर ऊँचाई और तिर्यक ऊँचाई है। तब OP = h और AC = BD = l.

लंब वृत्तीय शंकु के छिन्नक को दो लंबवृत्तीय शंकुओं के बराबर VAB और VCD के अंतर के रूप में देखा जा सकता है।

मान लीजिए शंकु VAB की ऊँचाई h₂ और तिर्यक ऊँचाई l है। अर्थात् VP = h₂ और VA = VB = l₁.

∴ शंकु VCD की ऊँचाई = VP – OP
= h₁ – h

क्योंकि समकोण त्रिभुज VOD और VPB समरूप हैं

⇒

शंकु की ऊँचाई VCD = h₁ – h

शंकु VAB के छिन्नक ACDB का आयतन

= शंकु (V AB) का आयतन – शंकु (V CD) का आयतन

अतः शंकु के छिन्नक का आयतन

पुनः यदि A₁ और A₂ (A₁ > A₂)

दो वृत्ताकार आधारों के पृष्ठीय क्षेत्रफल हैं।

A₁ = ????R² और A₂ = ????r²

अब शंकु के छिन्नक का आयतन

इस पोस्ट में आपको Ncert solutions class 10 maths chapter 13 pdf download ncert solutions class 10 maths chapter 13 pdf in hindi Class 10 Maths Chapter 13, Surface Areas and Volumes, Exercise 13.5 Class 10 Maths Chapter 13 Exercise 13.5 Surface area and volume Class 10 Solutions Surface area and volume Class 10 Notes कक्षा 10 गणित प्रश्नावली 13.5 पृष्ठीय क्षेत्रफल और आयतन Class 10 पृष्ठीय क्षेत्रफल एवं आयतन प्रश्नावली 13.5 से संबंधित पूरी जानकारी दी गई है अगर इसके बारे में आपका कोई भी सवाल या सुझाव हो तो नीचे कमेंट करके हम से जरूर पूछें और अगर आपको यह जानकारी फायदेमंद लगे तो अपने दोस्तों के साथ शेयर जरूर करें.

Class 10 Maths Chapter 13. पृष्ठीय क्षेत्रफल और आयतन Exercise 13.1
Class 10 Maths Chapter 13. पृष्ठीय क्षेत्रफल और आयतन Exercise 13.2
Class 10 Maths Chapter 13. पृष्ठीय क्षेत्रफल और आयतन Exercise 13.3
Class 10 Maths Chapter 13. पृष्ठीय क्षेत्रफल और आयतन Exercise 13.4
Class 10 Maths Chapter 13. पृष्ठीय क्षेत्रफल और आयतन Exercise 13.5

NCERT Solutions For Class 10th Maths पृष्ठीय क्षेत्रफल और आयतन (प्रश्नावली 13.5)

Related Posts

Leave a Comment Cancel Reply