Class 10 Maths Chapter 13 Exercise 13.4 – पृष्ठीय क्षेत्रफल और आयतन

Class 10 Maths Chapter 13 Exercise 13.4 – पृष्ठीय क्षेत्रफल और आयतन

NCERT Solutions for Class 10 Maths Chapter 13 Surface Areas And Volumes Ex 13.4 – जो विद्यार्थी 10वीं कक्षा में पढ़ रहे है उनके लिए यहां पर एनसीईआरटी कक्षा 10 गणित अध्याय 13. (पृष्ठीय क्षेत्रफल और आयतन) प्रश्नावली 13.4 के लिए सलूशन दिया गया है. जोकि एक सरल भाषा में दिया है .ताकि विद्यार्थी को पढने में कोई दिक्कत न आए .इसकी मदद से आप अपनी परीक्षा में अछे अंक प्राप्त कर सकते है. इसलिए निचे आपको एनसीईआरटी समाधान कक्षा 10 गणित अध्याय 13 पृष्ठीय क्षेत्रफल और आयतन प्रश्नावली 13.4 दिया गया है .

NCERT Solutions For Class 10th Maths पृष्ठीय क्षेत्रफल और आयतन (प्रश्नावली 13.4)

(जब तक अन्यथा न कहा जाए, लीजिए।)

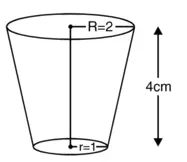
ऊपरी सिरे की त्रिज्या (R) = 2 cm
निचले सिरे की त्रिज्या (r) = 1 cm
गिलास की ऊँचाई (H) = 14 cm
गिलास छिन्नक के आकार का है
छिन्नक का आयतन

गिलास का आयतन = 102.67 cm³ उत्तर

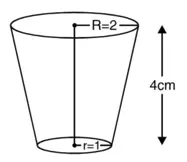
मान लीजिए ऊपरी सिरे और निचले सिरे की त्रिज्या R और r है।
ऊपरी सिरे की परिधि = 18 cm

2????R = 18 cm

निचले सिरे की परिधि = 6 cm
2????r = 6 cm
छिन्नक का वक्र पृष्ठीय क्षेत्रफल
= ????[R + r]l

= 12 x 4 cm²
= 48 cm²

छिन्नक का वक्र पृष्ठीय क्षेत्रफल

= 48 cm. उत्तर

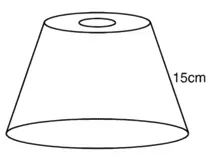
छिन्नक के निचले सिरे की त्रिज्या (R) = 10 cm
छिन्नक के ऊपरी सिरे की त्रिज्या (r) = 4 cm
छिन्नक की तिर्यक ऊँचाई (l) = 15 cm

छिन्नक का वक्र पृष्ठीय क्षेत्रफल

= ????l[R + r]

= 22 x 15 x 2 cm²

= 660 cm²

बंद सिरे का क्षेत्रफल

प्रयुक्त पदार्थ का कुल क्षेत्रफल = छिन्नक का वक्र पृष्ठीय क्षेत्रफल + बंद सिरे का क्षेत्रफल

= 660 cm² + 50.28 cm²
= 710.28 cm²

अतः प्रयुक्त पदार्थ का कुल क्षेत्रफल

= 710.28 cm² उत्तर

बर्तन के ऊपरी सिरे की त्रिज्या (R) = 20 cm
बर्तन के निचले सिरे की त्रिज्या (r) = 8 cm
बर्तन की ऊँचाई (H) = 16 cm

तिर्यक ऊँचाई

= √256 + 144 cm

तिर्यक ऊँचाई (I) = √400 cm = √20 x 20 cm
= 20 cm

बर्तन की धारिता

= 3.14 x 16 x 624 cm³

= 10449.92 ³

∴ बर्तन में दूध का आयतन

= 10449.92 cm³

∴ बर्तन में दूध का आयतन = 10.45 लिटर
1 लिटर का मूल्य = ₹ 20
∴ 10.45 लिटर का मूल्य = ₹ 20 x 10.45
दूध का मूल्य = ₹ 209

छिन्नक का वक्र पृष्ठीय क्षेत्रफल

= ????L[R + r] = 3.14 x 20 [20 + 8] cm ²
= 3.14 x 20 x 28 cm ²
= 1758.4 cm²

बर्तन के आधार का क्षेत्रफल = ????r²

= 3.14 x (8)² – cm²
= 3.14 x 64 cm²
= 200.96 cm²

बर्तन बनाने के लिए प्रयुक्त धातु = छिन्नक का वक्र पृष्ठीय क्षेत्रफल + आधार का क्षेत्रफल

= (1758. 4 + 200.96) cm²
= 1959.36 cm²

100 cm² धातु की चादर का मूल्य = ₹ 8

1 cm² धातु की चादर का मूल्य = ₹

1959.36 cm² धातु की चादर का मूल्य

= ₹

= ₹ 156.748
= ₹ 156.75

अतः धातु की चादर का कुल मूल्य

= ₹ 156.75
और दूध का कुल मूल्य ₹ 209 है।

5. 20 cm ऊँचाई और शीर्ष कोण (vertical angle) 60° वाले एक शंकु की ऊँचाई के बीचो-बीच से होकर जाते हुए एक तल से दो भागों में काटा गया है, जबकि तल शंकु के आधार के समांतर है। यदि इस प्राप्त शंकु के छिन्नक को व्यास वाले एक तार के रूप में परिवर्तित किया जाता है, तो तार की लंबाई ज्ञात कीजिए।

शंकु का शीर्षलम्ब शीर्ष कोण को द्विभाजित करता है।

∠EOF = 30°

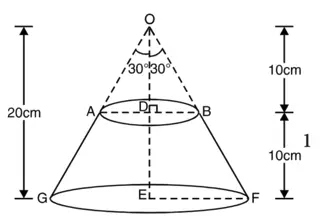
∆ODB में,

∆OEF में,

शंकु के छिन्नक का आयतन

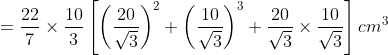
छिन्नक का आयतन

छिन्नक की तार बनाई गई है जो कि बेलनाकार होती है तथा जिसका व्यास है।

∴ बेलनाकार तार की त्रिज्या (r₁)

मान लीजिए इस प्रकार बने तार की लंबाई

= H cm

रूप बदलने पर भी आयतन समान ही रहता है। छिन्नक का आयतन = बेलनाकार तार का आयतन

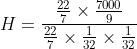
बेलनाकार तार की लंबाईं H = 796444.44 cm

= 7964.44 m

अतः, बेलनाकार तार की लंबाई = 7964.44 m उत्तर

इस पोस्ट में आपको Class 10 Maths Exercise 13.4 Surface Area and Volume class 10 maths chapter 13 pdf, surface area and volume class 10 pdf with answers ,Class 10 Maths Chapter 13 Ex 13.4 questions with solutions Class 10 Maths Surface Area and Volume Exercise 13.4 कक्षा 10 गणित अध्याय 13.4 पृष्ठीय क्षेत्रफल और आयतन कक्षा 10 गणित प्रश्नावली 13.4 के प्रश्न उत्तर एनसीईआरटी कक्षा-10 प्रश्नावली 13.4 गणित 13.पृष्ठीय क्षेत्रफल और आयतन से संबंधित पूरी जानकारी दी गई है अगर इसके बारे में आपका कोई भी सवाल या सुझाव हो तो नीचे कमेंट करके हम से जरूर पूछें और अगर आपको यह जानकारी फायदेमंद लगे तो अपने दोस्तों के साथ शेयर जरूर करें.

Class 10 Maths Chapter 13. पृष्ठीय क्षेत्रफल और आयतन Exercise 13.1
Class 10 Maths Chapter 13. पृष्ठीय क्षेत्रफल और आयतन Exercise 13.2
Class 10 Maths Chapter 13. पृष्ठीय क्षेत्रफल और आयतन Exercise 13.3
Class 10 Maths Chapter 13. पृष्ठीय क्षेत्रफल और आयतन Exercise 13.4
Class 10 Maths Chapter 13. पृष्ठीय क्षेत्रफल और आयतन Exercise 13.5