Class 10 Maths Chapter 12 Exercise 12.2 – वृत्तों से संबंधित क्षेत्रफल
NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles Ex 12.2 – आज हम आप के लिए Class 10 Maths Chapter 12 वृत्तों से संबंधित क्षेत्रफल लेकर आयें है। जो कि Class 10 Maths Exams के लिए अत्यन्त उपयोगी साबित होगी. कक्षा 10वीं के विद्यार्थी के लिए यहां पर एनसीईआरटी कक्षा 10 गणित अध्याय 12. (वृत्तों से संबंधित क्षेत्रफल) प्रश्नावली 12.2 के लिए सलूशन दिया गया है. जोकि एक सरल भाषा में दिया है .ताकि विद्यार्थी को पढने में कोई दिक्कत न आए .इसकी मदद से आप अपनी परीक्षा में अछे अंक प्राप्त कर सकते है.
NCERT Solutions For Class 10th Maths वृत्तों से संबंधित क्षेत्रफल (प्रश्नावली 12.2)
(जब तक अन्यथा न कहा जाए, ![]() का प्रयोग कीजिए)
का प्रयोग कीजिए)
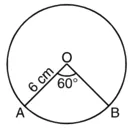
केंद्रीय कोण (0) = 60°
त्रिज्याखंड का क्षेत्रफल ![]()
![]()
![]()
∴ त्रिज्याखंड का क्षेत्रफल = 18.86 cm2 उत्तर
2????R = 22 cm
![]()
![]()
केंद्रीय कोण [चतुर्थांश] (θ) = 90°
∴ चतुर्थांश का क्षेत्रफल
![]()
![]()
चतुर्थांश का क्षेत्रफल = 9.625 cm2 उत्तर
प्रश्न 3. एक घड़ी की मिनट की सुई की लंबाई 14 cm है। इस सुई द्वारा 5 मिनट में रचित क्षेत्रफल ज्ञात कीजिए।
हल : मिनट की सुई की लंबाई
= वृत्त की त्रिज्या (R) = 14 cm
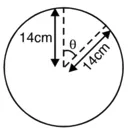
हमें ज्ञात है,
60′ = 360°
![]()
5′ = 6° x 5 = 30°
त्रिज्याखंड कोण (θ) = 30°
∴ सुई द्वारा 5 मिनट में रचित क्षेत्रफल
![]()
![]()
![]()
![]()
सुई द्वारा 5 मिनट में रचित क्षेत्रफल
= 51.33 cm2. उत्तर
(i) संगत लघु वृत्तखंड
(ii) संगत दीर्घ त्रिज्याखंड (???? = 3.14 का प्रयोग कीजिए)।
हल :वृत्त की त्रिज्या (R) = 10 cm
केंद्रीय कोण (θ) = 90°
लघु त्रिज्याखंड का क्षेत्रफल ![]()
![]()
लघु त्रिज्याखंड का क्षेत्रफल ![]()
लघु वृत्तखंड का क्षेत्रफल
= लघु त्रिज्याखंड का क्षेत्रफल – ∆AOB
![]() का क्षेत्रफल
का क्षेत्रफल
![]()
= (78.5 – 50) cm2
= 28.5 cm2
∴ लघु वृत्तखंड का क्षेत्रफल = 28.5 cm2 उत्तर
दीर्घ त्रिज्याखंड का क्षेत्रफल ![]()
![]()
![]()
![]()
∴ दीर्घ त्रिज्याखंड का क्षेत्रफल = 235.5 cm2 उत्तर
(ii) चाप द्वारा बनाए गए त्रिज्याखंड का क्षेत्रफल
(iii) संगत जीवा द्वारा बनाए गए वृत्तखंड का क्षेत्रफलहल :(i) वृत्त की त्रिज्या (R) = 21 cm
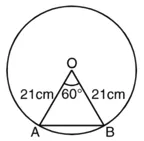
केंद्रीय कोण (θ) = 60°
चाप की लंबाई ![]()
![]()
चाप की लंबाई = 22 cm उत्तर
(ii) चाप द्वारा बनाए गए त्रिज्याखंड का क्षेत्रफल
![]()
![]()
= 231 cm2
∴ त्रिज्याखंड का क्षेत्रफल क्योंकि ∆OAB समबाहु त्रिभुज है जिसमें θ = 60°.
(iii) वृत्तखंड का क्षेत्रफल = त्रिज्याखण्ड का क्षेत्रफल – ∆AOB का क्षेत्रफल
![]() (भुजा)2
(भुजा)2
![]()
= (231 – 0.4325 x 441) cm2
= (231 – 190.7325) cm2
वृत्तखंड का क्षेत्रफल
= 40.26cm2 उत्तर
केंद्रीय कोण (θ) = 60°
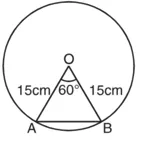
∆OAB में, केंद्रीय कोण θ = 60°
OA = OB = 15 cm
∴ ∠A = ∠B = 60°
∴ ∆OAB समबाहु त्रिभुज है।
![]() (भुजा)2
(भुजा)2
![]()
![]()
![]()
![]()
![]()
![]()
लघु वृत्तखंड का क्षेत्रफल = 20.43 cm2
दीर्घ वृत्तखंड का क्षेत्रफल = वृत्त का क्षेत्रफल – लघु वृत्तखंड का क्षेत्रफल
= ????R2 – 20.43 cm2
= (3.14 x 15 x 15 – 20.43) cm2
= (706.5 – 20.43) cm2
= 686.07 cm2
दीर्घ वृत्तखंड का क्षेत्रफल = 686.07 cm2 उत्तर
केंद्रीय कोण (θ) = 120°
∆OAM में, OM ⊥ AB
∴ ![]()
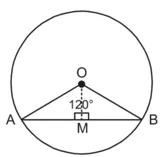
∴ ∠AOM = 60° = ∠OBM
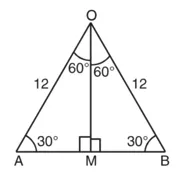
AB = 2AM
![]()
= (sin 60°) 12 cm
![]()
![]()
![]()
वृत्तखंड का क्षेत्रफल = त्रिज्याखंड का क्षेत्रफल – ∆OAB का क्षेत्रफल वृत्तखंड का क्षेत्रफल
![]()
![]()
![]()
= 150.72 cm2-36 x 1.73 cm2
= (150.72 – 62.28)cm2
= 88.44 cm2
∴ वृत्तखंड का क्षेत्रफल = 88.44 cm2 उत्तर
(देखिए आकृति। ज्ञात कीजिए :
(i) मैदान के उस भाग का क्षेत्रफल, जहाँ घोड़ा घास चर सकता है।
(ii) चरे जा सकने वाले क्षेत्रफल में वृद्धि, यदि घोड़े को 5 m लंबी रस्सी के स्थान पर 10 m लंबी रस्सी से बांध दिया जाए। (???? = 3.14 का प्रयोग कीजिए।)
(i) खूटे की रस्सी की लंबाई = वृत्त की त्रिज्या (R) = 5 m
केंद्रीय कोण (θ) = 90° [वर्ग का प्रत्येक कोण]
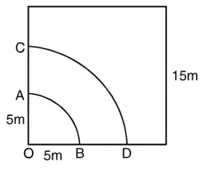
त्रिज्याखंड का क्षेत्रफल ![]()
![]()
त्रिज्याखंड का क्षेत्रफल ![]()
= 19.625 m2 उत्तर
(ii) जब त्रिज्याखंड की त्रिज्या 10 m हो जाती है।
त्रिज्याखंड OCD की त्रिज्या (R2) = 10 m
केंद्रीय कोण (θ) = 90°
∴ त्रिज्याखंड OCD का क्षेत्रफल ![]()
![]()
![]()
![]()
∴ चरे जा सकने वाले क्षेत्रफल में वृद्धि
= त्रिज्याखंड OCD का क्षेत्रफल
– त्रिज्याखंड OAB का क्षेत्रफल
= 78.5 m2 – 19.625 m2
= 58.875 m2
चरे जा सकने वाले क्षेत्रफल में वृद्धि
= 58.875 m2 उत्तर
(i) कुल वांछित चाँदी के तार की लंबाई
(ii) ब्रूच के प्रत्येक त्रिज्याखंड का क्षेत्रफल
वृत्त की त्रिज्या ![]()
व्यासों की संख्या = 5
बराबर त्रिज्याखंडों की संख्या = 10
(i) प्रयोग की गई तार की लंबाई = 5 व्यासों की लंबाई
+ वृत्त (ब्रूच) का परिमाप
= 5(35) mm + 2????R
![]()
= 175 mm + 110 mm
= 185 mm
(ii) ब्रूच के एक त्रिज्याखंड का कोण
= 360°/त्रिज्याखण्डों की संख्या
![]()
ब्रूच के प्रत्येक त्रिज्याखंड का क्षेत्रफल
![]()
![]()
![]()
= 96.25 mm
ब्रूच के प्रत्येक त्रिज्याखंड का क्षेत्रफल = 96.25 m2 उत्तर
तानों की संख्या = 8
केंद्रीय कोण (त्रिज्याखंड कोण) ![]()
त्रिज्याखंड का क्षेत्रफल ![]()
![]()
![]()
![]()
त्रिज्याखंड का क्षेत्रफल = 795.53 cm2
∴ छतरी के दो क्रमागत तानों के बीच का क्षेत्रफल
= 795.53 cm2 उत्तर
त्रिज्याखंड का कोण (0) = 115°
वाइपर त्रिज्याखंड के रूप में घूमता है।
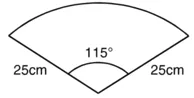
त्रिज्याखंड का क्षेत्रफल
= एक पत्ती द्वारा घूमा गया क्षेत्रफल
![]()
![]()
= 627.48 cm2
वाइपर की दो पत्तियों द्वारा घूमा गया क्षेत्रफल
= 2 X एक त्रिज्याखण्ड का क्षेत्रफल
= 2 x 627.48 cm2
= 1254.96 cm2 उत्तर
(???? = 3.14 का प्रयोग कीजिए।)
हल : त्रिज्याखंड कोण (θ) = 80°
त्रिज्याखंड की त्रिज्या (R) = 16.5 km
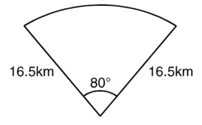
समुद्र के उस भाग का क्षेत्रफल जिसमें जहाज़ों को चेतावनी दी जा सकती है = त्रिज्याखंड का क्षेत्रफल
![]()
![]()
= 189.97 km 2
समुद्र के उस भाग का क्षेत्रफल जिसमें जहाजों को चेतावनी दी जा सकती है = 189.97 km2 उत्तर
डिज़ाइन की त्रिज्या (R) = 28 cm
प्रत्येक डिज़ाइन त्रिज्याखंड के आकार का है, केंद्रीय कोण ![]()
क्योंकि केंद्रीयकोण 60° है और OA = OB है।
∴ ∆OAB एक समबाहु त्रिभुज है जिसकी भुजा 28 cm है।
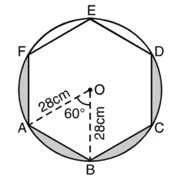
एक छायांकित डिज़ाइन भाग का क्षेत्रफल
= वृत्तखंड का क्षेत्रफल
= त्रिज्याखण्ड OAB का क्षेत्रफल – ∆OAB का क्षेत्रफल
![]() (भुजा)2
(भुजा)2
![]()
= (410.66 – 333.2)cm2
= 77.46 cm2
एक छायांकित डिज़ाइन भाग का क्षेत्रफल = 77.46 cm2
छः डिज़ाइन भागों का क्षेत्रफल
= 6 [एक डिज़ाइन भाग का क्षेत्रफल]
= 6 [77.46] cm2
= 464.76 cm2
1 cm2 डिज़ाइन बनाने का खर्च = ₹ 0.35
464.76 cm2 डिज़ाइन बनाने का खर्च
= ₹ 0.35 x 464.76
= ₹ 162.68
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
वृत्त की त्रिज्या = R
त्रिज्याखंड का क्षेत्रफल ![]()
![]()
![]()
∴ सही विकल्प (d) है। उत्तर
इस पोस्ट में आपको class 10 ncert maths exercise 12.2 solutions in hindi class 10 areas related to circles solutions pdf NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles Class 10 Maths Chapter 12 Areas Related to Circles Ex 12.2 NCERT Solutions for Class 10 Maths Exercise 12.2 एनसीईआरटी समाधान कक्षा 10 गणित प्रश्नावली 12.2 वृत्तों से संबंधित क्षेत्रफल Class 10 Maths वृतों से संबंधित क्षेत्रफल Ex 12.2 से संबंधित पूरी जानकारी दी गई है अगर इसके बारे में आपका कोई भी सवाल या सुझाव हो तो नीचे कमेंट करके हम से जरूर पूछें और अगर आपको यह जानकारी फायदेमंद लगे तो अपने दोस्तों के साथ शेयर जरूर करें.
NCERT Solutions for Class 10 Maths Chapter 12 वृत्तों से संबंधित क्षेत्रफल Exercise 12.1
NCERT Solutions for Class 10 Maths Chapter 12 वृत्तों से संबंधित क्षेत्रफल Exercise 12.2
NCERT Solutions for Class 10 Maths Chapter 12 वृत्तों से संबंधित क्षेत्रफल Exercise 12.3