Class 10 Maths Chapter 12 Exercise 12.3 – वृत्तों से संबंधित क्षेत्रफल
NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles Ex 12.3 – हर विद्यार्थी का सपना होता है कि वे अपनी कक्षा में अच्छे अंक से पास हो ,ताकि उन्हें आगे एडमिशन या किसी नौकरी के लिए फॉर्म अप्लाई करने में कोई दिक्कत न आए . कक्षा 10वीं के विद्यार्थी के लिए यहां परएनसीईआरटी कक्षा 10 गणित अध्याय 12. (वृत्तों से संबंधित क्षेत्रफल) प्रश्नावली 12.3 के लिए सलूशन दिया गया है. जोकि एक सरल भाषा में दिया है .ताकि विद्यार्थी को पढने में कोई दिक्कत न आए .इसकी मदद से आप अपनी परीक्षा में अछे अंक प्राप्त कर सकते है.
NCERT Solutions For Class 10th Maths वृत्तों से संबंधित क्षेत्रफल (प्रश्नावली 12.3)
(जब तक अन्यथा न कहा जाए, ![]() का प्रयोग कीजिए।)
का प्रयोग कीजिए।)
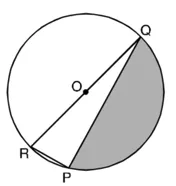
PR = 7 cm
RQ वृत्त का व्यास है।
∠RPQ = 90° अर्धवृत्त का कोण
समकोण ∆PQR में,
QR2 = RP2 + PQ2
![]()
= √625 cm
QR = 25cm
∴ वृत्त का व्यास (QR) = 25 cm
वृत्त की त्रिज्या ![]()
छायांकित भाग का क्षेत्रफल
= अर्धवृत्त का क्षेत्रफल – समकोण ∆RPQ का क्षेत्रफल
![]()
![]()
![]()
= (245.53 – 84) cm2 = 161.53 cm2
∴ छायांकित भाग का क्षेत्रफल = 161.53 cm2 उत्तर
बड़े वृत्त की त्रिज्या (R) = 14 cm
केन्द्रीय कोण ∠AOC (θ) = 40°
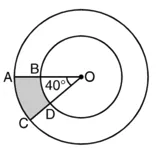
छायांकित भाग का क्षेत्रफल = बड़े वृत्तखंड OAC का क्षेत्रफल
– छोटे वृत्तखंड OBD का क्षेत्रफल
![]()
![]()
![]()
![]()
![]()
= 51.33 cm2
∴ छायांकित भाग का क्षेत्रफल = 51.33 cm2 उत्तर
अर्धवृत्त का व्यास (AB = BC)
= 14 cm
अर्धवृत्त की त्रिज्या (R) = 7 cm
वर्ग का क्षेत्रफल = (भुजा)2
= 14 x 14 cm2
= 196 cm2
अर्धवृत्त का क्षेत्रफल ![]()
![]()
= 77 cm2
दो अर्धवृत्तों का क्षेत्रफल = 2(77) cm2
= 154 cm2
छायांकित भाग का क्षेत्रफल
= वर्ग ABCD का क्षेत्रफल – दो अर्धवृत्तों का क्षेत्रफल
= (196 – 154) cm2
= 42 cm2
∴ छायांकित भाग का क्षेत्रफल = 42 cm2 उत्तर
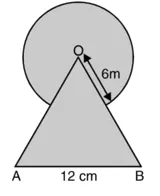
समबाहु त्रिभुज OAB की भुजा = 12 cm
OA = OB = AB = 12 cm
त्रिज्याखंड का केन्द्रीय कोण = 60°
[समबाहु त्रिभुज का प्रत्येक कोण 60°] वृत्त के दीर्घ त्रिज्याखंड का क्षेत्रफल
= वृत्त का क्षेत्रफल – त्रिज्याखंड का क्षेत्रफल
![]()
![]()
![]()
![]()
![]()
= 94.28 cm2
∴ वृत्त के दीर्घ त्रिज्याखंड का क्षेत्रफल
= 94.28 cm2
समबाहु त्रिभुज OAB का क्षेत्रफल
![]() (भुजा)2
(भुजा)2
![]()
= 1.73 x 36 cm2
= 62.28 cm2
छायांकित क्षेत्रफल = समबाहु त्रिभुज OAB का क्षेत्रफल
+ वृत्त के दीर्घ त्रिज्याखंड का क्षेत्रफल
= (62.28 + 94.28) cm2
= 156.56 cm2
छायांकित क्षेत्रफल
= 156.56 cm2 उत्तर
काटे गए प्रत्येक चतुर्थांश की त्रिज्या (r)
= 1 cm
वृत्त का व्यास (R) = 2 cm
∴ वृत्त की त्रिज्या (R) = 1 cm
वर्ग का क्षेत्रफल = (भुजा)2
= (4)2 cm2 = 16 cm2
4 चतुर्थांशों का क्षेत्रफल ![]()
![]()
= 3.14 cm2
वृत्त का क्षेत्रफल = ????R2
![]()
वृत्त का क्षेत्रफल = 3.14 cm2
अभीष्ट क्षेत्रफल = [वर्ग का क्षेत्रफल] – [4 चतुर्थांशों का क्षेत्रफल] – [वृत्त का क्षेत्रफल]
= (16 – 3.14 – 3.14) cm2
= 9.72 cm2
अभीष्ट क्षेत्रफल = 9.72 cm2 उत्तर
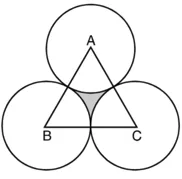
OA = OB = OC = 32 cm
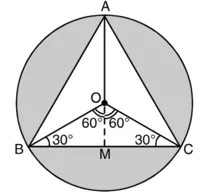
∆ABC एक समबाहु त्रिभुज है जिसमें
AB = AC = BC = 32 cm
∠A = ∠B = ∠C = 60°
∠AOB = ∠BOC = ∠AOC = 120°
OM ⊥ BC
![]()
∴ ∠O + ∠B + ∠C = 180°
120° + 2∠B = 180°
∠B = 30°
⇒ ∠B = ∠C = 30°
∴ समकोण ∆OMB में,
∠OBM = 30°
∴ ![]()
![]()
BM = 16√3 cm
∴ BC = 2MB = 32√3 cm
वृत्त का क्षेत्रफल ![]()
![]()
= 3218.28 cm2 उत्तर
∆ABC का क्षेत्रफल ![]() (भुजा)2
(भुजा)2
![]()
= 1328.64 cm2 उत्तर
∴ अभीष्ट क्षेत्रफल = वृत्त का क्षेत्रफल – ∆ABC का क्षेत्रफल
= (3218.28 – 1328.64) cm2
= 1889.64 cm2 उत्तर
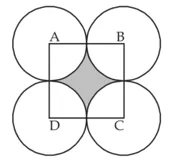
दिया गया है, ABCE एक वर्ग है जिसकी भुजा = 14 cm
चूँकि प्रत्येक वृत्त तीन शेष वृत्तों में से दो वृत्तों को बाह्य रूप से स्पर्श करता है,
अत: वृत्त की त्रिज्या = 14/2 = 7 cm
तब छायांकित भाग का क्षेत्रफल = ?
हम जानते हैं कि वर्ग का क्षेत्रफल = (भुजा)2
अत: दिये गये वर्ग का क्षेत्रफल = (14 cm)2
= 196 cm2
तथा कुल मिलाकर वृत्त के चार चतुर्थांश हैं
अत: वर्ग में पड़ने वाले वृत्त की संख्या = 1/4 वृत्त × 4 = 1 वृत्त
हम जानते हैं कि वृत्त का क्षेत्रफल = π r2
अत: वृत के चार चतुर्थांश अर्थात कुल 1 वृत्त का क्षेत्रफल
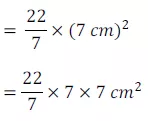
अत: वर्ग के अंदर पड़ने वाले वृत्त के चतुर्थांशों का कुल क्षेत्रफल = 154 cm2
अब छायांकत भाग का क्षेत्रफल = वर्ग का क्षेत्रफल – चारों वृत्त के चतुर्थांशों का क्षेत्रफल
= 196 cm2– 154 cm2
= 42 cm2
अत: छायांकित भाग का क्षेत्रफल = 42 cm2उत्तर
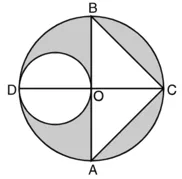
बड़े वृत्त की त्रिज्या, R = 7 cm
छोटे वृत्त का व्यास = 7 cm
∴ छोटे वृत्त की त्रिज्या
AB और CD एक वृत्त के दो परस्पर लंब व्यास हैं।
∴ AD ⊥ CD
बड़े वृत्त का क्षेत्रफल = ????R2
![]()
= 154 cm2
छोटे वृत्त का क्षेत्रफल = ????r2
![]()
= 38.50 cm2
∆ABC का क्षेत्रफल = ![]() आधार x ऊँचाई
आधार x ऊँचाई
![]()
= 49 cm2
∴ छायांकित क्षेत्रफल = बड़े वृत्त का क्षेत्रफल – छोटे वृत्त का क्षेत्रफल
– त्रिभुज का क्षेत्रफल
= (154 – 38.5 – 49) cm2
= 66.5 cm2 उत्तर
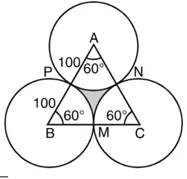
![]() (भुजा)2 = 17320.5 cm2
(भुजा)2 = 17320.5 cm2
(भुजा)2 ![]()
(भुजा)2 ![]()
भुजा = √4x100x100cm
भुजा = 2 X 100 cm = 200 cm
∴ AB = BC = AC
वृत्त की त्रिज्या ![]()
त्रिज्याखंड का कोण, θ = 60°
त्रिज्याखंड APN का क्षेत्रफल = ![]()
![]()
= 5233.33 cm2
तीनों त्रिज्याखंडों का क्षेत्रफल = 3 x 5233.33 cm2
= 15699.99 cm2
= 156700 cm2
∴ अभीष्ट छायांकित क्षेत्रफल = त्रिभुज का क्षेत्रफल – तीन त्रिज्याखंडों का क्षेत्रफल
= 17320.5 cm2 – 156700 cm2
= 1620.5 cm2
∴ छायांकित क्षेत्रफल = 1620.5 cm2 उत्तर
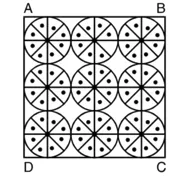
हल: वृत्त की त्रिज्या (R) = 7 cm
वृत्त का व्यास = 2 x R
= 2 x 7 cm
= 14 cm
क्योंकि वर्ग की भुजा के अनुदिश तीन वृत्त हैं।
∴ वर्ग की भुजा = 3 [14] cm = 42 cm2
रुमाल का कुल क्षेत्रफल = वर्ग का क्षेत्रफल = (भुजा)2
= (42)2 cm2 = 1764 cm2
9 वृत्ताकार डिज़ाइनों का क्षेत्रफल
= 9????R2
![]()
![]()
= 9 x 154 cm2
= 1386 cm2
∴ शेष भाग का अभीष्ट क्षेत्रफल
= वर्ग का क्षेत्रफल – 9 वृत्ताकार डिज़ाइनों का क्षेत्रफल
= 1764 cm2 – 1386 cm2
= 378 cm2
∴ शेष भाग का अभीष्ट क्षेत्रफल = 378 cm2 उत्तर
(ii) छायांकित भाग
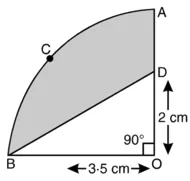
त्रिज्याखंड का कोण (θ) = 90°
OD = 2 cm.
(i) चतुर्थांश OACB का क्षेत्रफल = ![]()
![]()
= 9.625 cm2 उत्तर
(ii) ∆ODB का क्षेत्रफल = ![]() x आधार x ऊँचाई
x आधार x ऊँचाई
![]()
= 3.5 cm2
∴ छायांकित क्षेत्रफल = चतुर्थांश OACB का क्षेत्रफल
– ∆ODB का क्षेत्रफल
= (9.625 – 3.5) cm2
= 6.125 cm2
∴ छायांकित क्षेत्रफल = 6.125 cm2 उत्तर
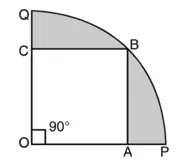
∠AOC = 90°
AB = OA
∴ ∆OAB में,
OB2 = OA2 + AB2
OB = √(20 cm)2 + (20 cm)2
= √400 cm2 + 400 cm2
= √800 cm2
OB = 20√2 cm
वर्ग OABC का क्षेत्रफल
= (भुजा)2 = (20)2 cm2
∴ वर्ग का क्षेत्रफल = 400 cm2
चतुर्थांश की त्रिज्या (R) = 20√2 cm2
त्रिज्याखंड का कोण (θ) = 90°
∴ त्रिज्याखंड का क्षेत्रफल ![]()
![]()
= 2 x 314 cm2
= 628 cm2
∴ अभीष्ट छायांकित क्षेत्रफल = त्रिज्याखंड का क्षेत्रफल – वर्ग का क्षेत्रफल
= (628 – 400) cm2
= 228 cm2 उत्तर
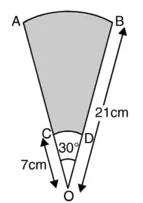
त्रिज्याखंड ODC की त्रिज्या (r) = 7 cm
त्रिज्याखंड का कोण (θ) = 30°
बड़े त्रिज्याखंड (OAB) का क्षेत्रफल
![]()
![]()
= 115.5 cm2
छोटे त्रिज्याखंड (ODC) का क्षेत्रफल
![]()
![]()
छोटे त्रिज्याखंड (ODC) का क्षेत्रफल = 12.83 cm2
अब छायांकित भाग का क्षेत्रफल = बड़े त्रिज्याखंड OAB का क्षेत्रफल
– छोटे त्रिज्याखंड OCD का क्षेत्रफल
= 115.5 cm2 – 12.83 cm2
= 102.66 cm2
छायांकित भाग का क्षेत्रफल = 102.66 cm2 उत्तर
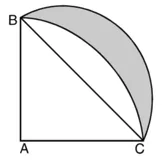
त्रिज्याखंड कोण (θ) = 90°
AB = AC = 7 cm
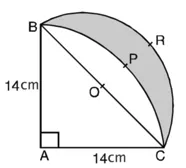
त्रिभुज का क्षेत्रफल ![]()
![]()
= 98 cm2
त्रिज्याखंड ACPB का क्षेत्रफल ![]()
![]()
= 154 cm2
∴ BOCPB का क्षेत्रफल = त्रिज्याखंड ABPC का क्षेत्रफल
– ∆ABC का क्षेत्रफल
= 154 cm2 – 98 cm2 = 56 cm2
∆ABAC में, AB2 + AC2 = BC2
(14 cm)2 + (14 cm)2 = BC2
BC = √196 + 196 cm = √2(196) cm
= 14√2 cm
∴ अर्धवृत्त BOCR की त्रिज्या ![]()
अर्धवृत्त का क्षेत्रफल ![]()
![]()
![]()
= 154 cm2
अभीष्ट क्षेत्रफल = अर्धवृत्त का क्षेत्रफल
– [BOCPB का क्षेत्रफल]
= 154 cm2 – 56 cm2 = 98 cm2
छायांकित भाग का क्षेत्रफल = 9.8 cm2 उत्तर
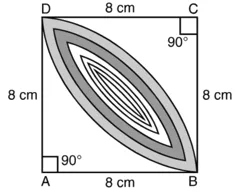
हल: वृत्तों से संबंधित क्षेत्रफल
वर्ग की भुजा = 8 cm
वर्ग का क्षेत्रफल = (8 cm)2 = 64 cm2
विकर्ण BD वर्ग ABCD को दो समान भागों में विभाजित करता है।
∆ABD का क्षेत्रफल = ∆ABDC का क्षेत्रफल
त्रिज्याखंड का कोण, θ = 90°
त्रिज्याखंड का क्षेत्रफल ![]()
![]()
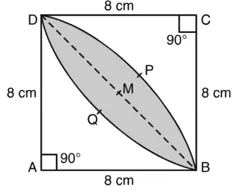
त्रिज्याखंड का क्षेत्रफल = 50.28 cm2
∆ABD का क्षेत्रफल ![]()
![]()
= 32 cm2
∴ वृत्तखंड DMBPD का क्षेत्रफल
= त्रिज्याखंड ABPD का क्षेत्रफल
– ∆ABD का क्षेत्रफल
= 50.28 cm2 – 32 cm2
= 18.28 cm2
छायांकित क्षेत्रफल = 2 वृत्तखंड DMBPD का क्षेत्रफल
= 2 (18.28) cm2 = 36.57 cm2 उत्तर
इस पोस्ट में आपको Class 10 Maths Chapter 12 Exercise 12.3 Areas Related to Circles class 10 ncert maths exercise 12.3 solutions in hindi Areas related to circles class 10 solutions pdf download Areas related to circles class 10 solutions pdf questions NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles Exercise 12.3 Class 10 Maths वृतों से संबंधित क्षेत्रफल Ex 12.3 कक्षा 10 गणित वृतों से सम्बंधित क्षेत्रफल प्रश्नावली 12.3 से संबंधित पूरी जानकारी दी गई है अगर इसके बारे में आपका कोई भी सवाल या सुझाव हो तो नीचे कमेंट करके हम से जरूर पूछें और अगर आपको यह जानकारी फायदेमंद लगे तो अपने दोस्तों के साथ शेयर जरूर करें.
NCERT Solutions for Class 10 Maths Chapter 12 वृत्तों से संबंधित क्षेत्रफल Exercise 12.1
NCERT Solutions for Class 10 Maths Chapter 12 वृत्तों से संबंधित क्षेत्रफल Exercise 12.2
NCERT Solutions for Class 10 Maths Chapter 12 वृत्तों से संबंधित क्षेत्रफल Exercise 12.3