Class 10 Maths Chapter 4 Exercise 4.4 – द्विघात समीकरण

Class 10 Maths Chapter 4 Exercise 4.4 – द्विघात समीकरण

NCERT Solutions for Class 10 Maths Chapter 4 Quadratic Equations Ex 4.4 – जो विद्यार्थी 10वीं कक्षा में पढ़ रहे है उनके लिए यहां पर एनसीईआरटी कक्षा 10 गणित अध्याय 4. (द्विघात समीकरण) प्रश्नावली 4.4 के लिए सलूशन दिया गया है. जोकि एक सरल भाषा में दिया है .ताकि विद्यार्थी को पढने में कोई दिक्कत न आए .इसकी मदद से आप अपनी परीक्षा में अछे अंक प्राप्त कर सकते है. इसलिए निचे आपको एनसीईआरटी समाधान कक्षा 10 गणित अध्याय 4 द्विघात समीकरण प्रश्नावली 4.4 दिया गया है .

NCERT Solutions For Class 10th Maths द्विघात समीकरण (प्रश्नावली 4.4)

(i) 2x² – 3x + 5 = 0
(ii) 3x² – 4√3x + 4= 0
(iii) 2x² – 6x + 3 = 0

2????² – 3???? + 5 = 0
इसकी तुलना
α????² + b???? + c = 0 से करने पर,
∴ α = 2, b = – 3, c = 5
D = b² – 4αc
= (-3)² – 4 x 2 x 5
= 9 – 40
= – 31 < 0
अतः दी गई द्विघात समीकरण का कोई वास्तविक मूल नहीं है। उत्तर

3????² – 4√3???? + 4 = 0

इसकी तुलना α????² + b???? + c = 0 से करने पर,
α = 3, b = – 4√3, c = 4
D = b² – 4αc
= (- 4√3)² – 4x3x4
= 48 – 48 = 0
अतः दी गई समीकरण के मूल वास्तविक और बराबर हैं।उत्तर

अब,

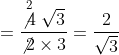
अतः दी गई द्विघात समीकरण के मूल हैं। के मूल हैं और हैं। है उत्तर

2????² – 6???? + 3 = 0
इसकी तुलना α????² + b???? + c = 0 से करने पर,
∴ α = 2, b = – 6, c = 3
D = b² – 4αc
= (- 6)² – 4 x 2 x 3
= 36 – 24
= 12 > 0

∴ दी गई द्विघात समीकरण के मूल वास्तविक और भिन्न हैं।

अब,

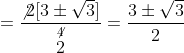
और

अतः दी गई द्विघात समीकरण के मूल और हैं। उत्तर

(i) 2x² + kx + 3 = 0
(ii) kx (x – 2) + 6 = 0

2????² + k???? + 3 = 0
इसकी तुलना α????² + b???? + c = 0 से करने पर,
∴ α = 2, b = k, c = 3
∵ दी गई द्विघात समीकरण के मूल बराबर हैं। .:.
∴ D = 0
b² – 4αc = 0
या (k)² – 4 x 2 x 3 = 0
या k² – 24 = 0
या k² = 24
या k = ± √24
या k = ± 2√6 उत्तर

k???? (???? – 2) + 6 = 0
या k????2 – 2k???? + 6 = 0
इसकी तुलना α????² + b???? + c = 0 से करने पर,
∴ α = k, b = – 2k, c = 6

∵ दी गई द्विघात समीकरण के मूल बराबर हैं।

∴ D = 0
b² – 4αc = 0
या (-2k)² – 4 x k x 6 =
या 4k² – 24k = 0
या 4k [k – 6] = 0
अर्थात् 4k = 0 या
k – 6 = 0
k = 0 या k = 6
k = 0, 6 उत्तर

आयताकार बगिया की लम्बाई = ???? m
और आयताकार बगिया की चौड़ाई = 2???? m
आयताकार बगिया का क्षेत्रफल = लम्बाई x चौड़ाई

= [???? x 2????] m²
= 2????² m²

प्रश्न के अनुसार,

2????² = 800

???? = ± √400
???? = ± 20

∵ आयत की लंबाई ऋणात्मक नहीं हो सकती।
इसलिए हम ???? = – 20 को छोड़ देते हैं
∴ ???? = 20
∴ आयताकार बगिया की चौड़ाई = 20 m
और आयताकार बगिया की लंबाई
= (2 x 20) m
= 40 m उत्तर

पहले मित्र की आयु = ???? वर्ष
और दूसरे मित्र की आयु = (20 – ????) वर्ष
चार वर्ष पूर्व,
पहले मित्र की आयु = (???? – 4) वर्ष
और दूसरे मित्र की आयु = (20 – ???? – 4) वर्ष

= (16 – ????) वर्ष

∴ उनका गुणनफल = (???? – 4) (16 – ????)
= 16???? – ????² – 64 + 4????
= – ????² + 20???? – 64

प्रश्न के अनुसार,

– ????² + 20???? – 64 = 48
या – ????² + 20???? – 64 – 48 = 0
या – ????² + 20???? – 112 = 0
या ????² – 20???? + 112 = 0

इसकी तुलना α????² + b???? + c = 0 से करने पर,

∴ α = 1, b = – 20, c = 112
अब D = b² – 4αc
= (- 20)² – 4 x 1 x 112
= 400 – 448
= – 48 < 0

∴ मूल वास्तविक नहीं हैं।

इसलिए, ???? का कोई मान द्विघात समीकरण (1) को संतुष्ट नहीं कर सकता। अतः दी गई स्थिति संभव नहीं हैं।

आयताकार पार्क की चौड़ाई = y m
∴ आयताकार पार्क का परिमाप = 2 (???? + y) m
और आयताकार पार्क का क्षेत्रफल = ????y m²
पहली शर्त के अनुसार,

2 (???? + y) = 80

y = 40 – x …..(1)
दूसरी शर्त के अनुसार,
????y = 400

???? (40 – ????) = 400 [(1) का प्रयोग करने पर]

या 40???? – ????² = 400
या 40???? – ????² – 400 = 0
या ????² – 40???? + 400 = 0

इसकी तुलना α????² + b???? + c = 0 से करने पर,

∴ α = 1, b = – 40, c = 400
D = b² – 4αc
= (- 40)² – 4 x 1 x 400
= 1600 – 1600 = 0

अब,

जब ???? = 20, तो (1) से
y = 40 – 20 = 20

∴ आयताकार पार्क की लंबाई और चौड़ाई का माप 20 m के बराबर है। अंत: दी गई आयताकार पार्क का अस्तित्व संभव है और यह एक वर्ग है।

इस पोस्ट में आपको class 10 maths chapter 4 exercise 4.4 question Class 10 Maths Ex 4.4 solutions Class 10 Maths Chapter 4 Solutions NCERT Solutions for Class 10 Maths Chapter 4 Quadratic Equations Ex 4.4 class 10 maths chapter 4 (द्विघात समीकरण) all examples एनसीईआरटी कक्षा-10 गणित 4. द्विघात गुणांक Class 10th maths chapter-4, द्विघात समीकरण प्रश्नावली 4.4 एनसीईआरटी समाधान कक्षा 10 गणित प्रश्नावली 4.4 कक्षा 10 प्रश्नावली 4.4 द्विघात समीकरण नोट्स से संबंधित पूरी जानकारी दी गई है अगर इसके बारे में आपका कोई भी सवाल या सुझाव हो तो नीचे कमेंट करके हम से जरूर पूछें और अगर आपको यह जानकारी फायदेमंद लगे तो अपने दोस्तों के साथ शेयर जरूर करें.

NCERT Solutions for Class 10 Maths Chapter 4 द्विघात समीकरण Exercise 4.1
NCERT Solutions for Class 10 Maths Chapter 4 द्विघात समीकरण Exercise 4.2
NCERT Solutions for Class 10 Maths Chapter 4 द्विघात समीकरण Exercise 4.3
NCERT Solutions for Class 10 Maths Chapter 4 द्विघात समीकरण Exercise 4.4