Class 10 Maths Chapter 4 Exercise 4.3 – द्विघात समीकरण

Class 10 Maths Chapter 4 Exercise 4.3 – द्विघात समीकरण

NCERT Solutions for Class 10 Maths Chapter 4 Quadratic Equations Ex 4.3 – कक्षा 10वीं के विद्यार्थी के लिए यहां पर एनसीईआरटी कक्षा 10 गणित अध्याय 4. (द्विघात समीकरण) प्रश्नावली 4.3 के लिए सलूशन दिया गया है. जोकि एक सरल भाषा में दिया है .ताकि विद्यार्थी को पढने में कोई दिक्कत न आए .इसकी मदद से आप अपनी परीक्षा में अछे अंक प्राप्त कर सकते है.

NCERT Solutions For Class 10th Maths द्विघात समीकरण (प्रश्नावली 4.3)

(i) 2x² – 7x + 3 = 0
(ii) 2x² + x – 4 = 0
(iii) 4x² + 4√3x + 3 = 0
(iv) 2x² + x + 4 = 0

हल : (i) दी गई द्विघात समीकरण है :

2????² – 7???? + 3 = 0
2????² – 7???? = – 3

या

या

या

या

या

या

स्थिति I

जब

या

या

स्थिति II

जब

या

या
अतः, दी गई द्विघात समीकरण के मूल हैं

(ii) दी गई द्विघात समीकरण है

2????² + ???? – 4 = 0

या 2????² + ???? = 4

या

या

या

या

या

या

या

स्थिति I. जब

या

या

स्थिति II.

जब

या

या

अतः, दी गई द्विघात समीकरण के मूल हैं : और उत्तर

(iii) दी गई द्विघात समीकरण है :

4????² + 4√3???? + 3 = 0

या 4????² + 4√3???? = – 3

या

या

या

या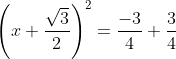

या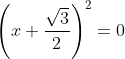

या

अर्थात्

या

या

अतः दी गई समीकरण के मूल और हैं। उत्तर

(iv) दी गई द्विघात समीकरण है :

2????² + ???? + 4 = 0

2????² + ???? = – 4
या

या

या

या

या

∵ किसी संख्या का वर्ग ऋणात्मक नहीं हो सकता।

इसलिए, के किसी भी वास्तविक मान के लिए ऋणात्मक नहीं हो सकता।

∴ यहाँ ???? का कोई भी वास्तविक मान नहीं है जो दी गई द्विघात समीकरण को संतुष्ट करता हो।
अतः, दिए गए समीकरण के कोई वास्तविक मूल नहीं हैं।

हल : (i) दी गई द्विघात समीकरण है :

2????² – 7???? + 3 = 0

इसकी α????² + b???? + c = 0 से तुलना करने पर,

α = 2, b = – 7, c = 3

अब, b² – 4αc = (-7)² – 4 x 2 x 3

= 49 – 24

= 25 > 0

∴

और

और

= 3 और

अतः, 3 और दी गई द्विघात समीकरण के मूल हैं।

(ii) दी गई द्विघात समीकरण है :

2????² + ???? – 4 = 0

इसकी तुलना α????² + b???? + c = 0 से करने पर,

α = 2, b = 1, c = – 4

अब, b² – 4αc = (1)² – 4 x 2 – (- 4)

= 1 + 32

= 33 > 0

∴

और

अंत:, और दी गई द्विघात समीकरण के मूल हैं।

(iii) दी गई द्विघात समीकरण है :

4????² + 4√3 + 3 = 0
इसकी तुलना α????² + b???? + c = 0 से करने पर,
∴ α = 4, b = 4√3, c = 3
अब, b² – 4αc = (4√3)² – 4 x 4 x 3
= 48 – 48 = 0

∴

अतः और दी गई द्विघात समीकरण के मूल हैं। उत्तर

(iv) दी गई द्विघात समीकरण है :

2????² + ???? + 4 = 0

इसकी तुलना α????² + b???? + c = 0 से करने पर,

∴ α = 2, b = 1, c = 4

अब, b² – 4αc = (1)² – 4 x 2 x 4

= 1 – 32 = – 31 < 0

परंतु

क्योंकि एक वास्तविक संख्या का वर्ग ऋणात्मक नहीं हो सकता। इसलिए ???? का कोई वास्तविक मान नहीं होगा। अतः दिए गए समीकरण का कोई वास्तविक मूल नहीं है।

(i)
(ii)

हल : (i) दी गई समीकरण है :

या

या ????² – 1 = 3????

या ????² – 3???? – 1 = 0

इसकी तुलना α????² + b???? + c = 0 से करने पर,

∴ α = 1, b = – 3, c = – 1

अब, b² – 4αc = (-3)² – 4. 1. (- 1)

= 9 + 4 = 13 > 0

∴

और

अतः, और दी गई द्विघात समीकरण के मूल हैं। उत्तर

हल : (i) दी गई समीकरण है :

या

या

या

या – 11 x 30 = 11 (????²– 3???? – 28)
या – 30 = ????²– 3???? – 28)
या ????² – 3???? – 28 + 30 = 0
या ????² – 3???? + 2 = 0
इसकी तुलना α????² + b???? + c = 0 से करने पर
∴ α = 1, b = – 3, c = 2
अब, b² – 4αc = (-3)² – 4 x 1 x 2
= 9 – 8
= 1 > 0

∴

और

और और 1

अतः, 2 और 1 दी गई द्विघात समीकरण के मूल हैं। उत्तर

हल : मान लीजिए, रहमान की वर्तमान आयु = ???? वर्ष

3 वर्ष पूर्व रहमान की आयु = (???? – 3) वर्ष
अब से 5 वर्ष पश्चात् रहमान की आयु = (???? + 5) वर्ष

प्रश्न अनुसार

या

या

या

या 6???? + 6 = ????²+2????-15

या ????² + 2???? – 15 – 6???? – 6 = 0
या ????² – 4???? – 21 = 0,
इसकी तुलना α????² + b???? + c = 0 से करने पर,
∴ α = 1, b = – 4, c = – 21
अब, b² – 4αc = (- 4)² – 4 x 1 x (-21)
= 16 + 84
= 100 > 0

∴

और

और

= 7 और – 3

∵ आयु ऋणात्मक नहीं हो सकती।
इसलिए हम ???? = – 3 को छोड़ देते हैं।
∴ ???? = 7
अतः, रहमान की वर्तमान आयु = 7 वर्ष। उत्तर

हल : मान लीजिए, शेफाली के गणित में प्राप्त अंक = ????

∴ शेफाली के अंग्रेज़ी में प्राप्त अंक = 30 – ????
पहली शर्त के अनुसार,
शेफाली के गणित में अंक = ???? + 2
और शेफाली के अंग्रेज़ी में अंक = 30 – ???? – 3
= 27 – ????
∴ उनका गुणनफल = (???? + 2) (27 – ????)
= 27???? – ????² + 54 – 2????
=-????² + 25???? + 54

प्रश्न की दूसरी शर्त अनुसार,

– ????² + 25???? + 54 = 210
या – ????² + 25???? + 54 – 210 = 0
या – ????² + 25???? – 156 = 0
या ????² – 25x + 156 = 0
इसकी तुलना α????²– + b???? + c = 0 से करने पर,
∴ α = 1, b = – 25, c = 156
अब, b² – 4αc = (-25)² – 4 x 1 x 156

= 625 – 624
= 1 > 0

∴

और

और

= 13 और 12

स्थिति I.

जब x = 13
तब शेफाली के गणित में अंक = 13
तथा शेफाली के अंग्रेजी में अंक = 30 – 13 = 17

स्थिति II.

जब x = 12
तब शेफाली के गणित में अंक = 12
शेफाली के अंग्रेज़ी में अंक = 30 – 12 = 18
अतः, शेफाली के दो विषयों में अंक हैं : 13 और 17 या 12 और 18

हल : मान लीजिए आयताकर खेत की छोटी भुजा= AD = ???? m
आयताकार खेत की लंबी भुजा = AB = (???? + 30) m
और आयताकार खेत का विकर्ण
= DB = (???? + 60) m
अब समकोण त्रिभुज DAB में,

पाइथागोरस प्रमेय का प्रयोग करने पर,

(DB)² = (AD)² + (AB)²
(????² + 60)² = (????)² + (???? + 30)²
या ????² + 3600 + 120????
= ????² + ????² + 900 + 60????
या ????² + 3600 + 120???? – 2????² – 900 – 60???? = 0
या – ????² + 60???? + 2700 = 0
????² – 60x – 2700 = 0

इसकी तुलना α????² + b???? + c = 0 से करने पर,

∴ α = 1, b = – 60, c = – 2700
और b² – 4αc = (- 60)² – 4 . 1 . (- 2700)
= 3600 + 10800
= 14400 > 0

∴

और

और

= 90 और – 30

∵ किसी भी भुजा की लंबाई ऋणात्मक नहीं होती।
इसलिए हम ???? = – 30 को छोड़ देते हैं।
∴ ???? = 90
अतः आयताकार खेत की छोटी भुजा
= 90 m
आयताकार खेत की लंबी भुजा
= (90 + 30) m
= 120 m Ans.

हल : मान लीजिए, बड़ी संख्या = ????

छोटी संख्या = y
प्रश्न की पहली शर्त अनुसार,
????² – y² = 180 …. (1)
प्रश्न की दूसरी शर्त अनुसार
y² = 8???? …. (2)
(1) और (2) से हम प्राप्त करते हैं,
????² – 8???? = 180
या ????² – 8???? – 180 = 0
इसकी तुलना α????² + b???? + c = 0 से करने पर,
∴ α = 1, b = – 8, c = – 180
और b² – 4αc = (- 8)² – 4 x 1 x (- 180)
= 64 + 720
= 784 > 0

∴

और

और

= 18 और – 10

जब ???? = – 10 तो, (2) से
y² = 8 (- 10) = – 80, जोकि संभव नहीं है।
इसलिए हम ???? = – 10 को छोड़ देते हैं।
जब ???? = 18, तो (2) से,
y² = 8 (18) = 144
या y = ±√144
या y = ± 12
अतः अभीष्ट संख्याएं 18 और 12
या 18 और – 12 हैं। उत्तर

हल : मान लीजिए रेलगाड़ी की एक समान चाल = ???? km/h

रेलगाड़ी द्वारा तय की गई दूरी = 360 km
रेलगाड़ी द्वारा लिया गया समय = दूरी/चाल
(∵ चाल = दूरी/चाल)

घंटे

रेलगाड़ी की बढ़ी हुई चाल = (???? + 5) km/h

∴ बढ़ी हुई चाल से रेलगाड़ी द्वारा लिया गया समय

घंटे

प्रश्न अनुसार,

या

या

या 1800 = ????² + 5????
या ????² + 5???? – 1800 = 0
इसकी तुलना α????² + b???? + c = 0 से करने पर,
∴ α = 1, b = 5, c = – 1800
और b² – 4αc = (5)² – 4 x 1 x (- 1800)
= 25 + 7200
= 7225 > 0

∴

और

और

= 40 और – 45
∵ किसी रेलगाड़ी की चाल ऋणात्मक नहीं हो सकती।
इसलिए, हम ???? = – 45 को छोड़ देते हैं।
∴ ???? = 40
अतः रेलगाड़ी की चाल = 40 km/h

हल : मान लीजिए, बड़े व्यास वाले नल द्वारा हौज को भरने में लिया समय = ???? घंटे

छोटे नल द्वारा हौज भरने में लिया समय = (???? + 10) घंटे
एक घंटे की स्थिति में,

बड़ा नल हौज भर सकता है

छोटा नल हौज भर सकता है

∴ बड़ा और छोटा दोनों नल हौज को भरते हैं …..(1)

परंतु दोनों नल एक साथ हौज भरने में समय लेते हैं घंटे

अब, दोनों नल एक साथ एक घंटे में हौज भर सकते हैं …..(2)

(1) और (2) से हम प्राप्त करते हैं,

या

या

या 75(2???? + 10) = 8 (????² + 10????)
या 150???? + 750 = 8????² + 80????
या 8????² + 80???? – 150x – 750 = 0
या 8????² – 70???? – 750 = 0
या 4????² – 35???? – 375 = 0

इसकी तुलना α????² + b???? + c = 0 से करने पर,

α = 4, b = – 35, c = – 375
और b² – 4αc = (- 35)² – 4 x 4 x (-375)
= 1225 + 6000
= 7225 > 0

∴

और

और

= 15 और

∵ समय ऋणात्मक नहीं हो सकता।
इसलिए, हम छोड़ देते हैं
∴ ???? = 15
अतः बड़े नल द्वारा हौज भरने के लिए लिया गया समय
= 15 घंटे
और छोटे नल द्वारा हौज भरने के लिए लिया गया समय
= (15 + 10) घंटे
= 25 घंटे उत्तर

हल : मान लीजिए सवारी गाड़ी का औसत चाल

= x km/h
एक्सप्रेस रेलगाड़ी की औसत चाल
= (x + 11) km/h
मैसूर और बैंगलोर के बीच की दूरी
= 132 km

सवारी गाड़ी द्वारा लिया गया समय घंटे

∵ चाल = दूरी/समय
एक्सप्रेस रेलगाड़ी द्वारा लिया गया समय

घंटे

प्रश्न अनुसार,

या

या

या 1452 = ????² + 11

या ????² + 11???? – 1452 = 0
इसकी तुलना α????² + b???? + c = 0 से करने पर,
α = 1, b = 11, c = – 1452
और b² – 4αc = (11)² – 4 x 1 x (- 1452)
= 121 + 5808
= 5929 > 0

∴

और

और

= 33 और – 44
∵ रेलगाड़ी की चाल ऋणात्मक नहीं हो सकती
∴ ???? = 33
अतः, सवारी गाड़ी की औसत चाल
= 33 km/h
और एक्सप्रेस रेलगाड़ी की औसत चाल
= (33 + 11) km/h
= 44 km/h

हल : पहले बड़े वर्ग की स्थिति मेंमान लीजिए वर्ग की भुजा की लंबाई
= ???? m
वर्ग का क्षेत्रफल = ????² m²
वर्ग का परिमाप = 4???? m
छोटे वर्ग की स्थिति में
मान लीजिए वर्ग की भुजा की लंबाई
= y m
वर्ग का क्षेत्रफल = y² m²
वर्ग का परिमाप = 4y m
प्रश्न की पहली शर्त के अनुसार,
????² + y????² = 468 ….(1)
दूसरी शर्त के अनुसार,
4???? – 4y = 24
या 4 (???? – y) = 24
या ???? – y = 6
या ???? = 6 + y ….(2)
(1) और (2) से हम प्राप्त करते हैं,
(6 + y)² + y² = 468
या 36 + y² + 12y + y² = 468
या 2y² + 12y + 36 – 468 = 0
या 2y² + 12y – 432 = 0
या y² + 6y – 216 = 0

इसकी तुलना αy² + by + c = 0 से करने पर,

α = 1, b = 6, c = – 216
और b² – 4αc = (6)² – 4 x 1 x (- 216)
= 36 + 864
= 900 > 0

∴

और

और

= 12 और – 18
∵ वर्ग की भुजा की लंबाई ऋणात्मक नहीं हो सकती।
इसलिए हम y = – 18 को छोड़ देते हैं।
∴ y = 12
(2) से, ???? = 6 + 12 = 18
अतः, दो वर्गों की भुजाएँ 12 m और 18 m हैं उत्तर

इस पोस्ट में आपको NCERT Class 10 Maths Ex 4.3 solutions , chapter 4 maths class 10 extra questions ,Class 10 Maths Exercise 4.3 NCERT solutions in Hindi NCERT Solutions Quadratic Equations Exercise 4.3 Class 10 Maths Solutions Chapter 4 द्विघात समीकरण Ex 4.3 ,कक्षा 10 गणित अध्याय 4.3 के लिए एनसीईआरटी समाधान Class 10 Maths Chapter 4 – Quadratic Equations एनसीईआरटी समाधान कक्षा 10 गणित प्रश्नावली 4.3 से संबंधित पूरी जानकारी दी गई है अगर इसके बारे में आपका कोई भी सवाल या सुझाव हो तो नीचे कमेंट करके हम से जरूर पूछें और अगर आपको यह जानकारी फायदेमंद लगे तो अपने दोस्तों के साथ शेयर जरूर करें.

NCERT Solutions for Class 10 Maths Chapter 4 द्विघात समीकरण Exercise 4.1
NCERT Solutions for Class 10 Maths Chapter 4 द्विघात समीकरण Exercise 4.2
NCERT Solutions for Class 10 Maths Chapter 4 द्विघात समीकरण Exercise 4.3
NCERT Solutions for Class 10 Maths Chapter 4 द्विघात समीकरण Exercise 4.4