Class 9 Maths Chapter 1 – संख्या पद्धति
NCERT Solutions for Class 9 Mathematics Chapter 1. संख्या पद्धति – कक्षा 9वीं के विद्यार्थियों के लिए जो अपनी क्लास में सबसे अच्छे अंक पाना चाहता है उसके लिए यहां पर एनसीईआरटी कक्षा 9th गणित अध्याय 1.( संख्या पद्धति ) के लिए समाधान दिया गया है. इस NCERT Solutions For Class 9 Mathematics Chapter 1. Number Systems की मदद से विद्यार्थी अपनी परीक्षा की तैयारी कर सकता है और परीक्षा में अच्छे अंक प्राप्त कर सकता है. इसे आप अच्छे से पढ़े यह आपकी परीक्षा के लिए फायदेमंद होगा .हमारी वेबसाइट पर Class 9 Mathematics के सभी चेप्टर के सलुसन दिए गए है .
| Class | Class 9 |
| Subject | Mathematics |
| Chapter | Chapter 1 |
| Chapter Name | संख्या पद्धति |
NCERT Solutions For Class 9 गणित Chapter 1 संख्या पद्धति
Class 9 Mathematics संख्या पद्धति Ex 1.1
Class 9 Mathematics संख्या पद्धति Ex 1.2
Class 9 Mathematics संख्या पद्धति Ex 1.3
Class 9 Mathematics संख्या पद्धति Ex 1.4
Class 9 Mathematics संख्या पद्धति Ex 1.5
Class 9 Mathematics संख्या पद्धति Ex 1.6
Class 9 Mathematics संख्या पद्धति (प्रश्नावली 1.1)
के रूप में लिख सकते हैं, जहाँ p और q पूर्णाक हैं और q ≠ 0 है ?हल : हाँ, शून्य एक परिमेय संख्या है और इसे रूप में इस प्रकार से लिख सकते हैं,
जहाँ p = 0
और q = 1
ध्यान दीजिए कि q कोई भी संख्या हो सकती है जो आप चाहते हैं।
इत्यादि]
हल : मान लीजिए 4 = 3, और b = 4
3 और 4 के बीच की परिमेय संख्या है।
अर्थात् = 
अब 3 और 
के बीच परिमेय संख्या
और 4 के बीच परिमेय संख्या
और के बीच परिमेय संख्या
और 
के बीच परिमेय संख्या
के 
बीच परिमेय संख्या
अतः छः परिमेय संख्याएँ हैं :
वैकल्पिक विधि :
एक अन्य विकल्प है कि एक ही चरण में सभी छ: परिमेय संख्याओं को ज्ञात कर लें। क्योंकि हम छ: संख्याएँ ज्ञात करना चाहते हैं इसलिए हम 6 + 1 अर्थात् 7 को हर लेकर 3 और 4 को परिमेय संख्याओं के रूप में लिखते हैं :
अर्थात् 
तब 3 और 4 के बीच छ: परिमेय संख्याएँ हैं :
और 
के बीच पाँच परिमेय संख्याएँ ज्ञात कीजिए।हल : हम जानते हैं कि 
∴ पाँच परिमेय संख्याएं हैं :
0.61, 0.62, 0.63, 0.64, 0.65
वैकल्पिक विधि :
∴ पांच परिमेय संख्याएं हैं : 
चेतावनी : हरों को बराबर बनाते समय इस बात का ध्यान रखना चाहिए कि उनके अंशों में समुचित अंतर हो, जिससे के हम पाँच परिमेय संख्याएं लिख सकें।
(i) प्रत्येक प्राकृत संख्या एक पूर्ण संख्या होती है।
(ii) प्रत्येक पूर्णांक एक पूर्ण संख्या होती है।
(iii) प्रत्येक परिमेय संख्या एक पूर्ण संख्या होती है।
हल : (i) सत्य है।
कारण : क्योंकि पूर्ण संख्याओं के संग्रह में सभी प्राकृत संख्याएँ होती हैं।
पूर्ण संख्या
अतः प्रत्येक पूर्ण संख्या प्राकृत संख्या नहीं होती परंतु प्रत्येक प्राकृत संख्या एक पूर्ण संख्या होती है। संख्या पद्धति
(ii) असत्य है।
कारण : ऋणात्मक संख्याएँ – 3, – 2, – 1 पूर्ण संख्याएं नहीं हैं।
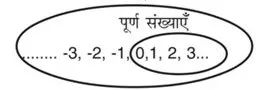
(iii) असत्य है।
परिमेय संख्याएँ हैं :
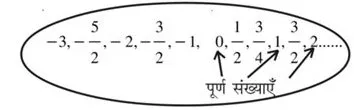
कारण :
पूर्ण संख्याएँ परिमेय संख्याओं का भाग हैं।
अतः प्रत्येक परिमेय संख्या पूर्ण संख्या नहीं है।
उदाहरण के लिए 
एक परिमेय संख्या है, परंतु पूर्ण संख्या नहीं है।
Class 9 Mathematics संख्या पद्धति Ex 1.1
Class 9 Mathematics संख्या पद्धति Ex 1.2
Class 9 Mathematics संख्या पद्धति Ex 1.3
Class 9 Mathematics संख्या पद्धति Ex 1.4
Class 9 Mathematics संख्या पद्धति Ex 1.5
Class 9 Mathematics संख्या पद्धति Ex 1.6