Class 7 Maths Chapter 1 Exercise 1.1 – पूर्णांक

Class 7 Maths Chapter 1 Exercise 1.1 – पूर्णांक

NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.1 – जो विद्यार्थी 7वीं कक्षा में पढ़ रहे है उनके लिए यहां पर एनसीईआरटी कक्षा 7 गणित अध्याय 1. (पूर्णांक) प्रश्नावली 1.1 के लिए सलूशन दिया गया है. जोकि एक सरल भाषा में दिया है .ताकि विद्यार्थी को पढने में कोई दिक्कत न आए .इसकी मदद से आप अपनी परीक्षा में अछे अंक प्राप्त कर सकते है. इसलिए निचे आपको एनसीईआरटी समाधान कक्षा 7 गणित अध्याय 1 पूर्णांक प्रश्नावली 1.1 दिया गया है .

NCERT Solutions For Class 7th Maths पूर्णांक (प्रश्नावली 1.1)

[su_note]1. किसी विशिष्ट दिन विभिन्न स्थानों के तापमानों को डिग्री सेल्सियस (C) में निम्नलिखित संख्या रेखा द्वारा दर्शाया गया है :[/su_note]

• (a) इस संख्या रेखा को देखिए और इस पर अंकित स्थानों के तापमान लिखिए।
• (b) उपर्युक्त स्थानों में से सबसे गर्म और सबसे ठंडे स्थानों के तापमानों में क्या अंतर है?
• (c) लाहुलस्पीति एवं श्रीनगर के तापमानों में क्या अंतर है?
• (d) क्या हम कह सकते हैं कि शिमला और श्रीनगर के तापमानों का योग शिमला के तापमान से कम है? क्या इन दोनों स्थानों के
  तापमानों का योग श्रीनगर के तापमान से भी कम है?

[su_label]हल :[/su_label]

(a) लाहुलस्पीति का तापमान = – 8°C
श्रीनगर का तापमान = – 2°C
शिमला का तापमान = 5°C
ऊटी का तापमान = 14°C
बैंगलोर का तापमान = 22°C

(b) सबसे गर्म स्थान का तापमान = 22°C
सबसे ठंडे स्थान का तापमान = – 8°C
सबसे गर्म और सबसे ठंडे स्थान में अंतर = 22 – (- 8)
= 22 + 8
= 30°C

(c) लाहुलस्पीति का तापमान = – 8°C
श्रीनगर का तापमान = – 2°C
लाहुलस्पीति और श्रीनगर के तापमान में अंतर = – 8 – (- 2)
= – 8 + 2
= – 6°C

(d) श्रीनगर और शिमला का तापमान = – 2 + 5 = 3°C
हाँ, श्रीनगर और शिमला दोनों का तापमान शिमला के तापमान से कम है परंतु यह श्रीनगर के तापमान से कम नहीं है।

[su_note]2. किसी प्रश्नोत्तरी में सही उत्तर के लिए धनात्मक अंक दिए जाते हैं और गलत उत्तर के लिए ऋणात्मक अंक दिए जाते हैं। यदि पाँच उत्तरोतर चक्करों (rounds) में जैक द्वारा प्राप्त किए गए अंक 25, -5, – 10, 15 और 10 थे, तो बताइए अंत में उसके अंकों का कुल योग कितना था?[/su_note]
[su_label]हल :[/su_label]

जैक के अंकों का योग = 25 + (- 5) + (- 10) + 15 + 10
= 25-5 – 10 + 15 + 10
= 25 + 15 + 10 – 5 – 10
= 50 – 15
= 35 उत्तर

[su_note]3. सोमवार को श्रीनगर का तापमान – 5°C था और मंगलवार को तापमान 2°C कम हो गया। मंगलवार को श्रीनगर का तापमान क्या था? बुधवार को तापमान 4°C बढ़ गया। बुधवार को तापमान कितना था ?[/su_note]

[su_label]हल :[/su_label] सोमवार का तापमान = – 5°C
∵ तापमान मंगलवार को 2°C कम हो गया था।
∴ मंगलवार का तापमान = – 5°C – 2°C
= – 7°C उत्तर
अब, ∴ बुधवार को तापमान 4°C बढ़ गया।
बुधवार का तापमान = – 7°C + 4°C
= – 3°C उत्तर

[su_note]4. एक हवाई जहाज़ समुद्र तल से 5000 मीटर की ऊँचाई पर उड़ रहा है। एक विशिष्ट बिंदु पर यह हवाई जहाज़ समुद्र तल से 1200 मीटर नीचे तैरती हुई पनडुब्बी के ठीक ऊपर है। पनडुब्बी और हवाई जहाज़ के बीच की ऊर्ध्वाधर दूरी कितनी है?[/su_note]
[su_label]हल :[/su_label] पनडुब्बी और हवाई जहाज़ के बीच की ऊर्ध्वाधर दूरी
= 5000 मीटर + 1200 मीटर
= 6200 मीटर
∴ पनडुब्बी और हवाई जहाज़ के बीच की ऊर्ध्वाधर दूरी 6200 मीटर उत्तर

[su_note]5. मोहन अपने बैंक खाते में 2000 रुपये जमा करता है और अगले दिन इसमें से 1642 रुपये निकाल लेता है। यदि खाते में से निकाली गई राशि को ऋणात्मक संख्या से निरूपित किया जाता है, तो खाते में जमा की गई राशि को आप कैसे निरूपित करोगे? निकासी के पश्चात् मोहन के खाते में शेष राशि ज्ञात कीजिए।[/su_note]
[su_label]हल :[/su_label] मोहन द्वारा जमा कराई गई राशि = 2000 रु०
मोहन द्वारा निकाली गई राशि = 1642 रु०
मोहन के खाते में शेष राशि = 2000 – 1642 रु०
= 358 रु० उत्तर
∴ निकाली गई राशि को ऋणात्मक संख्या से निरूपित किया जाता है।
∴ जमा की गई राशि को धनात्मक संख्या से निरूपित किया जाता है।

[su_note]6. रीता बिंदु A से पूर्व की ओर बिंदु B तक 20 किलोमीटर की दूरी तय करती है। उसी सड़क के अनुदिश बिंदु B से वह 30 किलोमीटर की दूरी पश्चिम की ओर तय करती है। यदि पूर्व की ओर तय की गई दूरी को धनात्मक पूर्णांक से निरूपित किया जाता है, तो पश्चिम की ओर तय की गई दूरी को आप कैसे निरूपित करोगे? बिंदु A से उसकी अंतिम स्थिति को किस पूर्णांक से निरूपित करोगे?[/su_note]

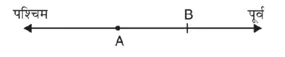
[su_label]हल :[/su_label]क्योंकि, रीता पहले पूर्व की ओर जाती है जिसे धनात्मक पूर्णांक से निरूपित किया जाता है फिर वह पश्चिम की ओर जाती है जो पूर्व के बिल्कुल उल्ट है। इसलिए, पश्चिम की ओर तय की गई दूरी ऋणात्मक पूर्णांक द्वारा निरूपित की जाती है।
बिंदु A से रीता की अंतिम स्थिति = 20 किलोमीटर – 30 किलोमीटर
= – 10 किलोमीटर
∴ रीता पूर्व की ओर 10 किलोमीटर है।
[su_note]8. a और b के निम्नलिखित मानों के लिए a – (- b) = a + b का सत्यापन कीजिए :[/su_note]

[su_row][su_column size=”1/2″ center=”no” class=””] (i)

5	-1	-4
-5	-2	7
0	3	-3

[/su_column] [su_column size=”1/2″ center=”no” class=””] (ii)

1	-10	0
-4	-3	-2
-6	4	-7

[/su_column][/su_row]
[su_label]हल :[/su_label]

(i) पहली पंक्ति का योग = 5 + (- 1) + (- 4)
= 5 – 1 – 4 = 4-4
= 0

दूसरी पंक्ति का योग = – 5 + (-2) + 7
= – 5 – 2 + 7 = – 7 +7

तीसरी पंक्ति का योग = 0 + 3 + (- 3)
= 0 + 3 – 3 = 3 – 3
= 0

पहले स्तंभ का योग = 5 + (-5) + 0
= 5 – 5 = 0

दूसरे स्तंभ का योग = (-1) + (-2) + 3
= – 1 – 2 + 3 = – 3 + 3 = 0

तीसरे स्तंभ का योग = (- 4) + 7 + (- 3)
= – 4 + 7 – 3
= 3 – 3 = 0

पहले विकर्ण का योग = 5 + (-2) + (-3)
= 5 – 2 – 3 = 5 – 5
= 0

दूसरे विकर्ण का योग = – 4 + (- 2) + 0
= – 4 – 2 = – 6

∵ प्रत्येक पंक्ति, प्रत्येक स्तंभ और प्रत्येक विकर्ण का योग 0 है, परंतु दूसरे विकर्ण का योग – 6 है।
∴ वर्ग (i) मायावी वर्ग नहीं है।

(ii) पहली पंक्ति का योग = 1 + (- 10) + 0
= 1 – 10 = – 9

दूसरी पंक्ति का योग = (- 4) + (- 3) + (- 2)
= – 4 – 3 – 2 = – 9

तीसरी पंक्ति का योग = (- 6) + 4 + (- 7)
= – 6 + 4 – 7
= – 2 – 7 = – 9

पहले स्तंभ का योग = 1 + (- 4) + (- 6)
= 1 – 4 – 6 = 1 – 10 = – 9

दूसरे स्तंभ का योग = (- 10) + (- 3) + 4
= – 10 -3 + 4 = – 13 +4
= – 9

तीसरे स्तंभ का योग = 0 + (- 2) + (-7)
= 0 – 2 – 7 = – 9

पहले विकर्ण का योग = 1 + (- 3) + (- 7)
= 1 – 3 – 7 = 1 – 10
= – 9

दूसरे विकर्ण का योग = 0 + (-3) + (-6)
= 0 – 3 – 6
= – 9
∴ प्रत्येक पंक्ति, प्रत्येक स्तंभ, प्रत्येक विकर्ण का योग – 9 है।
∴ वर्ग (ii) मायावी वर्ग है।

[su_note]8. a और b के निम्नलिखित मानों के लिए a – (- b) = a + b का सत्यापन कीजिए :[/su_note]
(i) a = 21, b = 18
(ii) a = 118, b = 125
(iii) a = 75, b = 84
(iv) a = 28, b = 11

[su_label]हल :[/su_label]

(i) पहली पंक्ति का योग = 5 + (- 1) + (- 4)
∴ α – (- b) = 21 – (-18)
= 21 + 18 = 39
और α + b = 21 + 18 = 39
∴ α – (- b) = α + b

अतः, सत्यापित हुआ।

(ii) दिया है, α = 118, b = 125
∴ α – (- b) = 118 – (- 125)
= 118 + 125 = 243
और α + b = 118 + 125 = 243
∴ α – (- b) = α + b

अतः, सत्यापित हुआ।

(iii) दिया है, α = 75, b = 84
α – (- b) = 75 – (- 84)
= 75 + 84 = 159
और α + b = 75 + 84 = 159
∴ α – (- b) = α + b

अतः, सत्यापित हुआ।

(iv) दिया है, α = 28, b = 11
α – (- b) = 28 – (-11)
= 28 + 11 = 39
और α + b = 28 + 11 = 39
∴ α – (- b) = α + b
अतः, सत्यापित हुआ।

[su_note]9. निम्नलिखित कथनों को सत्य बनाने के लिए, बॉक्स में संकेत >, < अथवा = का उपयोग कीजिए :[/su_note]
(a) (- 8) + (- 4) ???? (-8) – (-4)
(b) (-3) + 7 – (19) ???? 15 – 8 + (-9)
(c) 23 – 41 + 11 ???? 23 – 41 – 11
(d) 39 + (- 24) – (15) ???? 36 + (- 52) – (-36)
(e) – 231 + 79 + 51 ???? – 399 + 159 + 81

[su_label]हल :[/su_label]  (a) (-8) + (-4) < (-8) – (-4)
(b) (-3) +7 – (19) < 15 – 8 + (-9)
(c) 23 – 41 + 11 > 23 – 41 – 11
(d) 39 + (-24) – (15) < 36 + (-52) – (-36)
(e) – 231 + 79 + 51 >- 399 + 159 + 81

[su_note]10. पानी के एक तालाब में अंदर की ओर सीढ़ियाँ हैं। एक बंदर सबसे ऊपर वाली सीढ़ी (यानी पहली सीढ़ी) पर बैठा हुआ है। पानी नौवीं सीढ़ी पर है।[/su_note]

(i) वह एक छलाँग में तीन सीढ़ियाँ नीचे की ओर और अगली छलाँग में दो सीढ़ियाँ ऊपर की ओर जाता है। कितनी छलाँगों में वह पानी के स्तर तक पहुँच पाएगा?

(ii) पानी पीने के पश्चात् वह वापिस जाना चाहता है। इस कार्य के लिए वह एक छलाँग में 4 सीढ़ियाँ ऊपर की ओर और अगली छलाँग में 2 सीढ़ियाँ नीचे की ओर जाता है। कितनी छलाँगों में वह वापस सबसे ऊपर वाली सीढ़ी पर पहुँच जाएगा?

(iii) यदि नीचे की ओर पार की गई सीढ़ियों की संख्या को ऋणात्मक पूर्णांक से निरूपित किया जाता है और ऊपर की ओर पार की गई सीढ़ियों की संख्या को धनात्मक पूर्णांक से निरूपित किया जाता है, तो निम्नलिखित को पूरा करते हुए भाग (i) और (ii) में उसकी गति को निरूपित कीजिए :
(a) – 3 + 2 + ……….. = – 8
(b) 4 – 2 + ……. = 8. (a) में योग (- 8) आठ सीढ़ियाँ नीचे जाने को निरूपित करता है तो (b) में योग 8 किसको निरूपित करेगा?

[su_label]हल :[/su_label] मान लीजिए नीचे की ओर पार की गई सीढ़ियों की संख्या को ऋणात्मक पूर्णांक से निरूपित किया जाता है। ऊपर की ओर पार की गई सीढियों की संख्या को धनात्मक पूर्णांक से निरूपित किया जाता है। ऊपर और नीचे की ओर की सीढ़ियों की कुल संख्या = 9

(i) एक छलाँग में नीचे की ओर पार की गई सीढ़ियों की संख्या = 3
एक छलाँग में ऊपर की ओर पार की गई सीढ़ियों की संख्या = 2

प्रश्न के अनुसार, छलाँगों की संख्या जिसमें वह पानी के स्तर तक पहुँच जाएगा
= – 9 + (-3 + 2)
= – 10
अतः वह 10 छलाँगों में पानी के स्तर तक पहुँच जाएगा। उत्तर

(ii) एक छलाँग में ऊपर की ओर पार की गई सीढ़ियों की संख्या     = 4 – 2
एक छलाँग में नीचे की ओर पार की गई सीढ़ियों की संख्या            = – 2
∴ एक छलाँग में पार की गई सीढ़ियों की संख्या                           = 4 – 2
.                                                                                          = 2
अब, सबसे ऊपर वाली सीढ़ी के लिए तय की गई सीढ़ियाँ = 9
अतः, ऊपर वाली सीढ़ी पर वह 5 छलाँगों में पहुँच जाएगा। उत्तर

(iii) (a) -3 + 2 -3 + 2 – 3 + 2 – 3 + 2 – 3 + 2 – 3 = – 8
(b) 4 – 2+ 4 – 2+ 4 = 8

इस पोस्ट में आपको Class 7 maths chapter 1 exercise 1.1 integers solutions NCERT Solutions for Class 7 Maths Chapter 1 Exercise 1.1 class 7 maths chapter 1 exercise 1.1 Integers ncert solutions for class 7 maths chapter 1 pdf class 7 maths chapter 1 exercise 1.1 solutions कक्षा 7 गणित अभ्यास 1.1 अध्याय 1 पूर्णांक एनसीईआरटी समाधान कक्षा 7 गणित प्रश्नावली 1.1 से संबंधित पूरी जानकारी दी गई है अगर इसके बारे में आपका कोई भी सवाल या सुझाव हो तो नीचे कमेंट करके हम से जरूर पूछें और अगर आपको यह जानकारी फायदेमंद लगे तो अपने दोस्तों के साथ शेयर जरूर करें.

NCERT Solutions for Class 7 Maths Chapter 1 पूर्णांक Exercise 1.1
NCERT Solutions for Class 7 Maths Chapter 1 पूर्णांक Exercise 1.2
NCERT Solutions for Class 7 Maths Chapter 1 पूर्णांक Exercise 1.3
NCERT Solutions for Class 7 Maths Chapter 1 पूर्णांक Exercise 1.4