Class 10 Maths Chapter 9 त्रिकोणमिति के कुछ अनुप्रयोग

Class 10 Maths Chapter 9 त्रिकोणमिति के कुछ अनुप्रयोग

NCERT Solutions Class 10 Maths Chapter 9 त्रिकोणमिति के कुछ अनुप्रयोग – 10वीं कक्षा के विद्यार्थियों के लिए जो अपनी क्लास में अच्छे अंक पाना चाहता है उसके लिए यहां पर एनसीईआरटी कक्षा 10th गणित अध्याय 9. ( त्रिकोणमिति के कुछ अनुप्रयोग) के लिए समाधान दिया गया है. इस NCERT Solutions For Class 10 Maths Chapter 9 Some Applications of Trigonometry की मदद से विद्यार्थी अपनी परीक्षा की तैयारी कर सकता है और परीक्षा में अच्छे अंक प्राप्त कर सकता है. इसे आप अच्छे से पढ़े यह आपकी परीक्षा के लिए फायदेमंद होगा .हमारी वेबसाइट पर Class 10 Maths के सभी चेप्टर के सलुसन दिए गए है .

NCERT Solutions For Class 10th Maths त्रिकोणमिति के कुछ अनुप्रयोग (प्रश्नावली 9.1)

हल : मान लीजिएAB खंभे की ऊंचाई है।
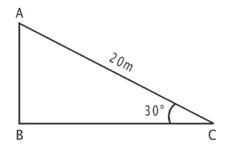
AC = 20 m डोर की लंबाई है।

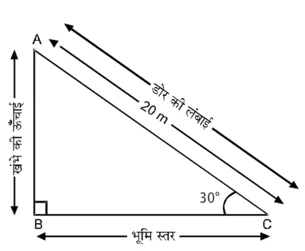
इस स्थिति में, उन्नयन कोण 30° है।
आकृति में विभिन्न आयोजन दिखाए गए हैं। समकोण ∆ABC में,

या

या

अतः खंभे की ऊँचाई 10 m. है। उत्तर

हल : मान लीजिए आँधी से पहले पेड़ की लंबाई BD है। आँधी के पश्चात्
AD = AC = टूटे गए पेड़ के भाग की लंबाई। आकृति में विभिन्न आयोजन दिखाए गए हैं।

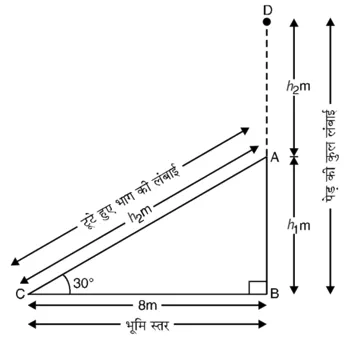
समकोण ∆ABC में,

या

या ….(1)

साथ ही,

या

या

…(2)

पेड़ की कुल लंबाई = h₁ + h₂

[(1) और (2) के प्रयोग से]

= 8√3 m

अतः, वृक्ष की ऊँचाई 8√3 m है। उत्तर

हल : स्थिति I. 5 वर्ष से कम उम्र के बच्चों के लिए

मान लीजिए AC = l₁ m फिसलनपट्टी की लंबाई को निरूपित करता है और BC = 1.5 m फिसलनपट्टी की ऊँचाई है। इस स्थिति में उन्नयन कोण 30° हैं।
आकृति में विभिन्न आयोजन दिखाए गए हैं।

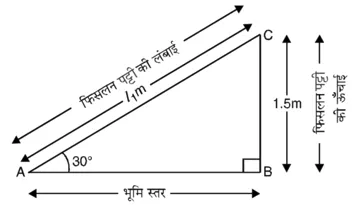
समकोण ∆ABC में,

या
या l₁ = 1.5m x 2 = 3m
स्थिति II. अधिक उम्र के बच्चों के लिये मान लीजिए AC = l₂m फिसलन पट्टी की लंबाई को निरूपित करता है और BC = 3 m फिसलनपट्टी की ऊँचाई है। इस स्थिति में उन्नयन कोण 60° का है। आकृति में विभिन्न आयोजन दिखाए गए हैं।

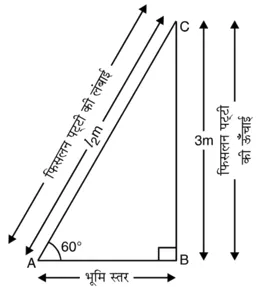
समकोण ∆ABC में,

या
या

अतः 5 वर्ष से कम उम्र तथा इससे अधिक उम्र के बच्चों के लिए फिसलनपट्टी की लंबाई है :
3 m और 2√3 m है। उत्तर

हल : मान लीजिए

BC = h m मीनार की ऊँचाई है और AB = 30 m भूमि स्तर पर दूरी है। विभिन्न आयोजन आकृति में दिखाए गए हैं

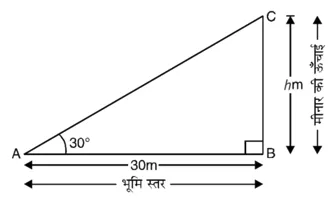
समकोण ∆ABC में,

या

या

= 10√3m = 10 x 1.732m

h = 17.32 m (लगभग)

अतः, मीनार की ऊँचाई 17.32 m. है। उत्तर

हल : मान लीजिए

पतंग बिंदु C पर स्थित है। AC = l m पतंग के साथ लगी डोरी की लंबाई है। इस स्थिति में उन्नयन कोण 60° है।
विभिन्न आयोजन आकृति में दिखाए गए हैं।

 

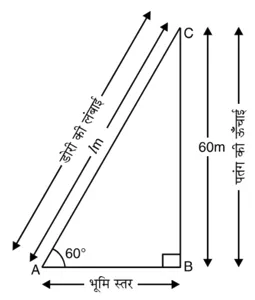
समकोण ∆ABC में,

या

या

अतः, डोरी की लंबाई 40√3 m है। उत्तर

[(1) और (2) का प्रयोग करने से]

अतः, लड़के द्वारा भवन की ओर तय की गई दूरी 19√3 m है ।

हल : मान लीजिए BC = 20 m भवन की ऊँचाई है और DC = h m संचार मीनार की ऊँचाई है। भवन के शिखर पर लगी संचार मीनार के आधार और शिखर के उन्नयन कोण क्रमश: 45° और 60° हैं।

विभिन्न आयोजन आकृति में दिखाए अनुसार हैं

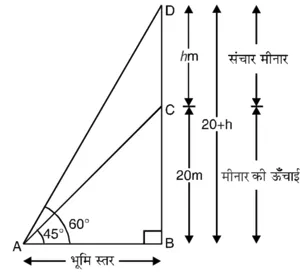
समकोण ∆ABC में,

या

या AB = 20 m …(1)

साथ ही, समकोण ∆ABD में,

या

या

या …..(2)

(1) और (2) से हमें प्राप्त होता है,

या 20√3 = 20 + h
या h = 20√3 – 20
या h = 20(√3 – 1) = 20 (1.732 – 1)
= 20 x 0.732 = 14.64
अतः, मीनार की ऊँचाई 14.64 m. है। उत्तर

हल : मान लीजिए

BC = h m पेडस्टल की ऊँचाई है और CD = 1.6 m मूर्ति की ऊँचाई है। भूमि के बिंदु से मूर्ति के शिखर और पेडस्टल के शिखर के उन्नयन कोण क्रमश: 60° और 45° हैं।
विभिन्न आयोजन आकृति में दिखाए अनुसार हैं।

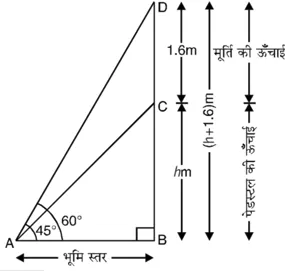
समकोण ∆ABC में,

या

या AB = h m …(1)

समकोण ∆ABD में,

या

या …..(2)

(1) और (2), से हमें प्राप्त होता है,

या √3h = h + 1.6

या (√3 – 1)h = 1.6

या

या

या

= 0.8×2.732 = 2.1856
= 2.20 (लगभग)
अतः, पेडस्टल की ऊँचाई 2.20 m है। उत्तर

हल : मान लीजिए

BC = 50 m मीनार की ऊँचाई है और AD = hm भवन की
ऊंचाई है। मीनार के पाद-बिंदु से भवन के शिखर का और भवन के पादबिंदु से मीनार के शिखर के उन्नयन कोण क्रमश: 30° और 60° हैं। विभिन्न आयोजन आकृति में दिखाए अनुसार हैं।

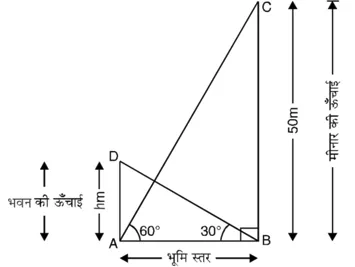
समकोण ∆ABC में,

या

या ….(1)

साथ ही, समकोण ∆DAB में,

या

या AB = h√3m …(2)

(1) और (2), से हमें प्राप्त होता है

या

या

या h = 16.70m (लगभग)
अतः, भवन की ऊँचाई 16.70 m है। उत्तर

हल : मान लीजिए

BC = DE = hm दो बराबर खंभों की ऊँचाई है और बिंदु A अभीष्ट बिंदु है जहाँ से दोनों खंभों के उन्नयन कोण क्रमश: 30° और 60° हैं। विभिन्न आयोजन आकृति में दिखाए अनुसार हैं।

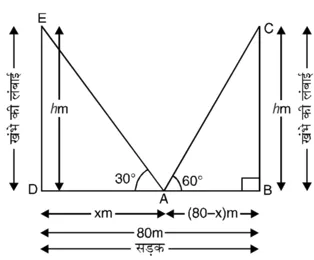
समकोण ∆ADE में,

या

या …(1)

समकोण ∆ABC में,

या

या h = (80 – ????)√3 ….(2)

(1) और (2) से, हमें प्राप्त होता है

या ???? = (80 – ????)√3 x √3

या ???? = (80 – ????)3

या ???? = 240 – 3????

या 4???? = 240

या

???? का मूल्य (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है।

∴ DA = ????m = 60 m

और AB = (80 – ????)m = (80 – 60)m = 20 m.
अतः, खंभे की ऊँचाई 34.64 m है और बिंदु की खंभों से दूरी क्रमशः
20 m और 60 m है।

हल : मान लीजिए

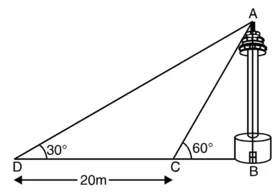
BC = ???? m नहर की चौड़ाई है और CD = hm टीवी टॉवर की ऊँचाई है। भिन्न-भिन्न स्थितियों में टॉवर के शिखर के उन्नयन कोण क्रमश: 30° और 60° हैं।

विभिन्न आयोजन आकृति में दिखाए अनुसार हैं।

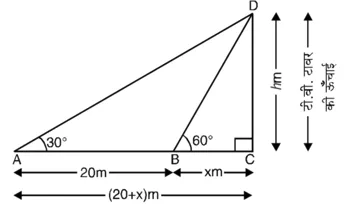
समकोण ∆BCD में,

या

या h = √3???? …(1)

साथ ही, समकोण ∆ACD में,

या

या …(2)

(1) और (2) से, हमें प्राप्त होता है

या 3???? = 20 + ????
या 2???? = 20
या
???? का मूल्य (1) में, प्रतिस्थापित करने पर हमें प्राप्त होता है :
h = 10(√3) = 10 x 1.732
h = 17.32
अत: टीवी टॉवर की ऊँचाई 17.32 m है और नहर की चौड़ाई 10 m. है। उत्तर

हल : मान लीजिए

BD = h m केबल टॉवर की ऊँचाई है और AE = 7 m भवन की ऊंचाई है। बिंदु E से केबल टॉवर के शिखर का उन्नयन कोण और पाद का अवनमन कोण क्रमशः 60° और 45° है।
विभिन्न आयोजन आकृति के अनुसार हैं।

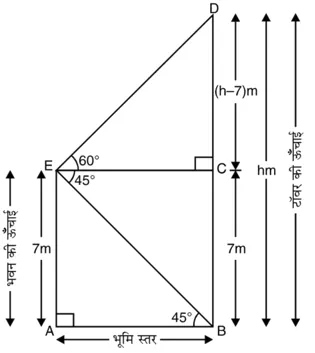
समकोण ∆BAE में,

या

या AB = 7 m …(1)

साथ ही, समकोण ∆DCE में,

या

या ….(2)

परंतु AB = EC …(दिया है)

∴

[(1) और (2) के प्रयोग से] या 7√3 = h – 7
या h = 7√3 + 7 = 7(√3 + 1)
या h = 7(1.732 + 1) = 7(2.732)
या h = 19.124
या h = 19.20 (लगभग)
अतः, केबल टॉवर की ऊंचाई 19.20 m है।

हल :

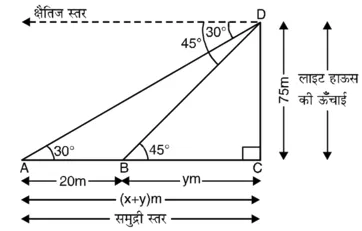
मान लीजिए CD = 75 m लाइट हाऊस की ऊँचाई है और लाइट हाऊस के शिखर के बिंदु D से दो जहाजों के अवनमन कोण क्रमश: 30° और 45° हैं। विभिन्न आयोजन आकृति में दिखाए अनुसार हैं।

समकोण ∆BCD में,

या

या y = 75 …(1)

साथ ही, समकोण ∆ACD में,

या

या ???? + y = 75√3

या ???? + 75 = 75√3

[(1) का प्रयोग करने पर]

या ???? = 75√3 – 75

= 75(√3 – 1)
= 75(1.732 – 1)
= 75(0.732)
या ???? = 54.90
अतः दो जहाजों के बीच की दूरी 54.90 m है।

हल : मान लीजिए

1.2 m लंबी लड़की की स्थिति ‘A’ है। इस बिंदु से विभिन्न दूरियों पर गुब्बारे के उन्नयन कोण क्रमश: 30° और 60° हैं। साथ ही, BE = CD = 88.2 m गुब्बारे की ऊंचाई है।

विभिन्न आयोजन आकृति में दिखाए अनुसार हैं:

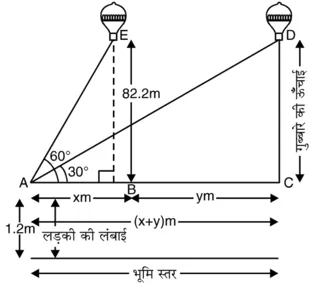
समकोण ∆ABE में,

या

या ….(1)

साथ ही, समकोण ∆ACD में,

या

या ???? + y = 88.2√3

या

या

या

या

या

या y = 58.8√3
या y = 58.8(1.732) = 101.8416
या y = 101.90

अतः, इस अंतराल के दौरान गुब्बारे द्वारा तय की गई दूरी 101.90 m. है।
उत्तर

हल : मान लीजिए

CD = hm मीनार की ऊँचाई है। मान लीजिए ‘A’ कार की
प्रारंभिक स्थिति है और छः सेकंड के बाद कार B पर पहुँच जाती है। A और B पर कार के अवनमन कोण क्रमश: 30° और 60° हैं। विभिन्न आयोजन आकृति में दिखाए अनुसार हैं।

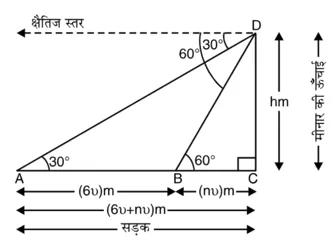
मान लीजिए कार की चाल ???? मीटर प्रति सेकंड है। सूत्र, दूरी = चाल x समय, का प्रयोग करने पर
AB = कार द्वारा 6 सेकंड में तय की गई दूरी
AB = 60 मीटर
साथ ही, कार द्वारा मीनार तक पहुँचने में लिया गया समय ‘n’ सेकंड है।
∴ BC = n???? मीटर
समकोण ∆ACD में,

या

या …(1)

साथ ही, समकोण ∆BCD में,

या

या h = n???? (√3) …(2)

(1) और (2) से, हमें प्राप्त होता है

या 6???? + n???? = n???? (√3 x √3)

या 6???? + n???? = 3n???? या 6???? = 2n????

या

अतः मीनार के पाद तक पहुँचने में कार द्वारा लिया गया साथ 3 सेकंड है। उत्तर

हल : मान लीजिए

CD = h m मीनार की ऊँचाई है और B ; A अभीष्ट बिंदु हैं
जो मीनार से क्रमश: 4 m और 9 m की दूरी पर हैं। विभिन्न आयोजन आकृति में दिखाए अनुसार हैं।

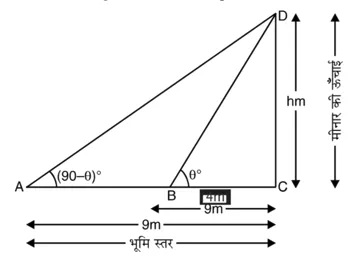
समकोण ∆BCD में,

या …(1)

साथ ही, समकोण ∆ACD में ,

या ….(2)

(1) और (2) को गुणा करने पर, हमें प्राप्त होता है।

या

या h² = 36 = (6)²

या h = 6
अतः, मीनार की ऊँचाई 6 m है।

इस पोस्ट में आपको Class 10 Maths Chapter 9 त्रिकोणमिति के कुछ अनुप्रयोग some applications of trigonometry class 10 pdf Class 10 maths chapter 9 some applications of trigonometry some applications of trigonometry class 10 notes Class 10 Maths Chapter 9 Exercise 9.1 Solutions Class 10 Maths Solutions Chapter 9 त्रिकोणमिति के कुछ अनुप्रयोग Ex 9.1. एनसीईआरटी समाधान कक्षा 10 गणित अध्याय 9 त्रिकोणमिति के कुछ अनुप्रयोग Trigonometry Case Study Questions Class 10 chapter 9 से संबंधित पूरी जानकारी दी गई है अगर इसके बारे में आपका कोई भी सवाल या सुझाव हो तो नीचे कमेंट करके हम से जरूर पूछें और अगर आपको यह जानकारी फायदेमंद लगे तो अपने दोस्तों के साथ शेयर जरूर करें.