Class 10 Maths Chapter 6 Exercise 6.6 – त्रिभुज

Class 10 Maths Chapter 6 Exercise 6.6 – त्रिभुज

NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.6 – जो विद्यार्थी 10वीं कक्षा में पढ़ रहे है उनके लिए यहां पर एनसीईआरटी कक्षा 10 गणित अध्याय 6. (त्रिभुज) प्रश्नावली 6.6 के लिए सलूशन दिया गया है. जोकि एक सरल भाषा में दिया है .ताकि विद्यार्थी को पढने में कोई दिक्कत न आए .इसकी मदद से आप अपनी परीक्षा में अछे अंक प्राप्त कर सकते है. इसलिए निचे आपको एनसीईआरटी समाधान कक्षा 10 गणित अध्याय 6 त्रिभुज प्रश्नावली 6.6 दिया गया है .

NCERT Solutions For Class 10th Maths त्रिभुज (प्रश्नावली 6.6)

[su_note note_color=”#eeeee9″ radius=”15″]प्रश्न 1. आकृति में, PS कोण ∠QPR का समद्विभाजक है।सिद्ध कीजिए कि काजिए[/su_note]  कि है।

[su_label]हल : दिया है : ∆PQR, PS कोण ∠QPR का समद्विभाजक है अर्थात् ∠1 = ∠2 है।[/su_label]

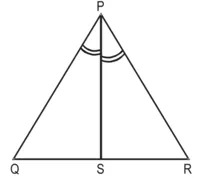
सिद्ध करना है

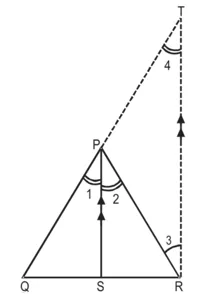
रचना : R में से एक रेखा PS के समांतर खींचिए जो QP को बढ़ाने पर T पर मिलती है।
उपपत्ति : ∆QRT में,

PS || TR
∠2 = ∠3 (एकांतर कोण)
∠1 = ∠4 (संगत कोण)
परन्तु ∠1 = ∠2 (दिया है)

∠3 = ∠4
∆PRT में,
∠3 = ∠4 (प्रमाणित)
PT = PR

[समान भुजाओं के सम्मुख कोण समान होते हैं।]

∆QRT में,
PS || TR

∴ [आधारभूत समानुपातिकता प्रमेय से]

(PT = PR)

[su_note note_color=”#eeeee9″ radius=”15″]प्रश्न 2. आकृति में D त्रिभुज ABC के कर्ण AC पर स्थित एक बिंदु है तथा DM ⊥ BC और DN ⊥ AB, सिद्ध कीजिए कि[/su_note]

(i) DM² = DN.MC
(ii) DN² = DM.AM.

[su_label]दिया है : ∆ABC में, DM ⊥ BC,[/su_label]
DN ⊥ AB है।

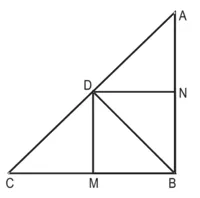
सिद्ध करना है : DM² = DN.AC
DN = DM.AM.

हल: BD ⊥ AC (दिया है)
⇒ ∠BDC = 90°
⇒ ∠BDM + ∠MDC = 90° ….(1)

∆DMC में,
∠DMC = 90°

[∵ DM ⊥ BC (दिया है)]

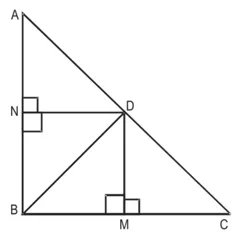
⇒ ∠C + ∠MDC = 90° …(2)
(1) और (2),
∠BDM + ∠MDC = ∠C + ∠MDC
∠BDM = ∠C

[दोनों ओर से ∠MDC को काटने पर]
अब ∆BMD और ∆MDC में,

∠BDM = ∠C [प्रमाणित]
∠BMD = ∠MDC [प्रत्येक 90°]
∆BMD ~ ∆MDC [AA समरूपता कसौटी से]

⇒

[∵ समरूप त्रिभुजों की संगत भुजाएं समानुपाती होती हैं।]
⇒ DM² = BM x MC
⇒ DM² = DN x MC
[∵ BM = DM]

इसी प्रकार ∆NDA ~ ∆NBD

⇒

[∵ समरूप त्रिभुजों की संगत भुजाएं समानुपाती होती हैं।]

⇒ DN² = BN x AN
⇒ DN² = DM x AN

[su_note note_color=”#eeeee9″ radius=”15″]प्रश्न 3. आकृति में ABC एक त्रिभुज है जिसमें ∠ABC > 90° है तथा AD ⊥ BC है। सिद्ध कीजिए कि[/su_note]

AC² = AB² + BC² + 2BC.BD है।

[su_label]हल : दिया है : ∆ABC में AD ⊥ BC जब BC का बढ़ाया जाता है। ∠ABC > 90° है।[/su_label]
सिद्ध करना है : AC² = AB² + BC² + 2BC.BD.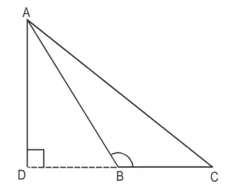

उपपत्ति : समकोण ∆ADB में,
AB² = BD² + AD² …(1)
[पाइथागोरस प्रमेय से]
अब, समकोण ∆ADC में,
AC² = AD² + DC²
= AD² + (DB + BC)
= AD² + BD + BC² + 2BC.BD [(1) से]
= AB² + BC² + 2BC.BD
अत: AC² = AB² + BC² + 2BC x BD.

[su_note note_color=”#eeeee9″ radius=”15″]प्रश्न 4. आकृति में, ABC एक त्रिभुज है जिसमें ∠ABC > 90° है तथा AD ⊥ BC है।[/su_note]
सिद्ध कीजिए कि :
AC² = AB² + BC² – 2BC.BD.

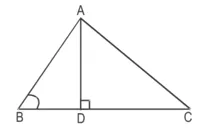
[su_label]हल : दिया है :[/su_label]

∆ABC जिसमें ∠ABC < 90° तथा AD ⊥ BC है।

सिद्ध करना है : AC² = AB² + BC² – 2BC.BD.

उपपत्ति : ADC एक समकोण है जिसमें D पर समकोण है।

AC² = CD + DA² …(1)

(पाइथागोरस प्रमेय से)

साथ ही, ∆ADB समकोण ∆ है D पर समकोण है।

AB² = AD² + DB² …(2)

(1) से हमें प्राप्त होता है

AC² = AD² + (CB – BD)²

= AD² + CB² + BD² – 2CB x BD

या AC² = (BD² + AD²) + CB² – 2CB x BD

AC² = AB² + BC² – 2BC x BD.

[(2) के प्रयोग से]

[su_note note_color=”#eeeee9″ radius=”15″]प्रश्न 5. आकृति में AD त्रिभुज ABC की एक माध्यिका है तथा AM I BC है[/su_note]

सिद्ध कीजिए कि :
(i)
(ii)
(iii)

[su_label]हल : दिया है : ∆ABC में, AM ⊥ BC, AD, ∆ABC की एक माध्यिका है।[/su_label]

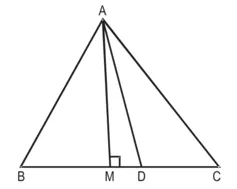
सिद्ध करना है :

(i)
(ii)
(iii)

उपपत्ति : ∆AMC में,

AC² = AM² + MC²
= AM² + (MD + DC)²
AC² = AM² + MD² + DC² + 2MD x DC

[समकोण त्रिभुज ∆AMD]

[AD² = AM² + MD²]

∴ ……(1)

[su_label](ii) समकोण त्रिभुज AMB में,[/su_label]

AB² = AM² + BM²
= AM² + (BD – MD)²

= AM² + BD² + MD² – 2BD x MD = (AM² + MD²) + BD²

[∵ ∆AMD में, AD² = MA² + MD²]

[su_label](iii) (1) और (2) को जोड़ने पर,[/su_label]

AB² = AC² = AD² + BC.MD

यह वांछित परिणाम है। [अतः सत्यापित

[su_note note_color=”#eeeee9″ radius=”15″]प्रश्न 6. सिद्ध कीजिए कि एक समांतर चतुर्भुज के विकर्णों के वर्गों का योग उसकी भुजाओं के वर्गों के योग के बराबर होता है।[/su_note]
[su_label]हल:[/su_label]

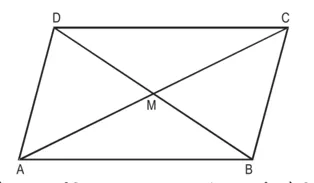
दिया है : मान लीजिए ABCD एक समांतर चतुर्भुज है जिसमें विकर्ण AC और BD परस्पर बिंदु M पर प्रतिच्छेद करते हैं।
सिद्ध करना है : AB² + BC² + CD² + DA²
= AB² + BC²

उपपत्ति : समांतर चतुर्भुज के विकर्ण एक-दूसरे को परस्पर विभाजित करते हैं।

∴ समांतर चतुर्भुज ABCD में,

विकर्ण BD और AC एक दूसरे को परस्पर काटते हैं।

या MB और MD क्रमश : त्रिभुज ABC और ADC की माध्यिका है।

हम जानते हैं, कि AD, ∆ABC की माध्यिका है,

इसका प्रयोग करते हुए,

…(1)

और …(2)

(1) और (2), को जोड़ने पर, हमें प्राप्त होता है,

AB² + BC² + AD² + CD²

AB² + BC² + AD² + CD²

AB² + BC² + AD² + CD² = BD² + AC²

अतः एक समांतर चतुर्भुज के विकर्णों के वर्गों का योग उसकी भुजाओं के वर्गों के योग के बराबर होता है।

[su_note note_color=”#eeeee9″ radius=”15″]प्रश्न 7. आकृति में, एक वृत्त की दो जीवाएँ AB और CD परस्पर बिंदु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि[/su_note]

(i) ∆APC ~ ∆DPB
(ii) AP.PB = CP.DP.

[su_label]हल : दिया है :[/su_label] एक वृत्त की दो जीवाएँ AB और CD परस्पर बिंदु P पर प्रतिच्छेद करती हैं।

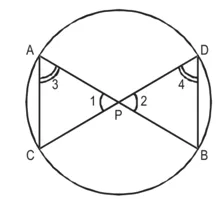
सिद्ध करना है : (i) ∆APC ~ ∆DPB

[su_label](ii) AP. PB = CP. DP.[/su_label]

उपपत्ति : (i) ∆APC और ∆DPB में,

∠1 = ∠2 (शीर्षाभिमुख कोण)

∠3 = ∠4 (एक ही वृत्तखंड के कोण)

∴ ∆APC ~ ∆DPB [AA समरूपता कटौती]

[su_label](ii) ∆APC ~ ∆DPB (ऊपर प्रमाणित)[/su_label]

(यदि दो त्रिभुजें समरूप हों, तो उनके संगत कोण समानुपाती होते हैं।)
AP.PB = PC.DP [अतः सत्यापित]

[su_note note_color=”#eeeee9″ radius=”15″]प्रश्न 8. आकृति में, एक वृत्त की दो जीवाएँ AB और CD बढ़ाने पर परस्पर बिंदु P पर प्रतिच्छेद करती हैं।[/su_note]
सिद्ध कीजिए कि :

(i) ∆PAC ~ ∆PDB
(ii) PA.PB = PC.PD.

[su_label]हल : दिया है :[/su_label]एक वृत्त की दो जीवाएँ AB और CD बढ़ाने पर परस्पर बिंदु P पर प्रतिच्छेद करती हैं।
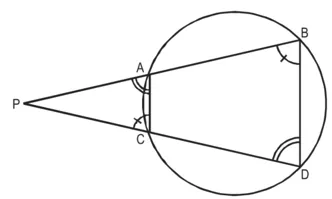
सिद्ध करना है : (i) ∆PAC ~ ∆PDB

[su_label](ii) PA.PB = PC.PD.[/su_label]

उपपत्ति : (i) ∆PAC और ∆PDB से,

∠P = ∠P (उभयनिष्ठ)

∠PAC = ∠PDB

(चक्रीय चतुर्भुज का बाह्य कोण अतः सम्मुख कोण के बराबर होता है।)

∴ ∆PAC ~ ∆PDB [AA समरूपता कसौटी से]

[su_label](iii) ∆PAB ~ ∆PDB[/su_label]

∴

[यदि तो त्रिभुजें समरूप हों, तो उनकी संगत भुजाएँ समानुपाती होती हैं।]

PA x PB = PC x PD.

[su_note note_color=”#eeeee9″ radius=”15″]प्रश्न 9. आकृति में, त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है

कि सिद्ध कीजिए कि : AD कोण ∠BAC का समद्विभाजक है। [/su_note]

[su_label]हल : दिया है :[/su_label]∆ABC, में भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि

सिद्ध करना है : AD कोण ∠BAC का समद्विभाजक है।

अर्थात्, ∠1 = ∠2

रचना : C में से CE || DA खींचिए जो BA को बढ़ाने पर E पर मिले।

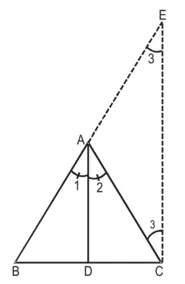
उपपत्ति : ∆BCE में,
AD || CE …(रचना)

आधारभूत समानुपातिकता प्रमेय से,

परंतु

∆ACE में,

⇒ AE = AC

⇒ ∠3 = ∠4 …. (बराबर भुजाओं के सम्मुख कोण)

चूँकि CE || DA और AC उन्हें प्रतिच्छेद करती है, तब

∠2 = ∠4 ..(एकांतर कोण)

साथ ही, CE || DA और BAE उन्हें प्रतिच्छेद करती है,

∠1 = ∠3 …(संगत कोण)

इस प्रकार, हमें प्राप्त करना है :

∠3 = ∠4

⇒ ∠4 = ∠1

∠3 = ∠1

परंतु ∠4 = ∠2

⇒ ∠1 = ∠2.

AD, LBAC को समद्विभाजित करता है।

[su_note note_color=”#eeeee9″ radius=”15″]प्रश्न 10. नाज़िमा एक नदी की धारा में मछलियाँ पकड़ रही है। उसकी मछली पकड़ने वाली छड़ का सिरा पानी की सतह से 1.8 m ऊपर है तथा डोरी के निचले सिरे से लगा कांटा पानी की सतह पर इस प्रकार स्थित है कि उसकी नाजिमा से दूरी 3.6 m है और छड़ के सिरे के ठीक नीचे पानी की सतह पर स्थित बिंदु से उसकी दूरी 2.4 m है। यह मानते हुए कि उसकी डोरी (उसकी छड़ के सिरे से काँटे तक ) तनी हुई है, उसने कितनी डोरी बाहर निकाली हुई है ( देखिए आकृति) ? यदि वह डोरी को 5 cm/s की दर से अंदर खींचे, तो 12 सेकंड के बाद नाजिमा की काँटे से क्षैतिज दूरी कितनी होगी?[/su_note]

[su_label]हल : समकोण त्रिभुज ABC में,[/su_label]
AB = 1.8 cm,
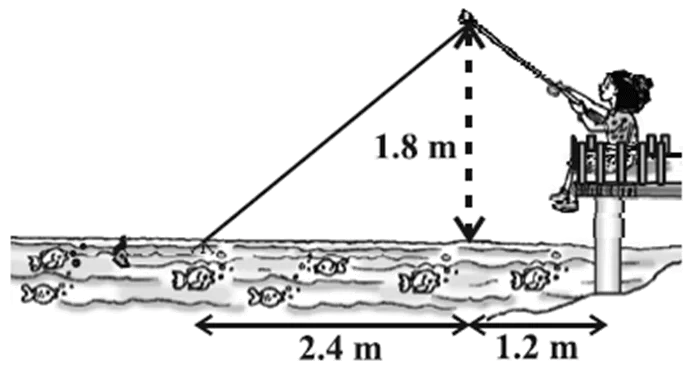
BC = 2.4 cm, ∠B = 90°
पाइथागोरस प्रमेय से,
AC² = AB² + BC²
AC² = (1.8)² + (2.4)²
AC² = 3.24 + 5.76 = 9
AC² = (3)²
AC = 3 cm
अब नाज़िमा डोरी को 5 cm/s की दर से अंदर खींचे, तो डोरी की लंबाई कम होती है।
= 5 x 12 = 60 cm
= 0.6 m ; 12 सेकण्ड में.
मान लो, 12 सेकण्ड के बाद काँटे की स्थिति D है।
∴ AD = AC – (12 सेकण्ड में तय दूरी)
= (3 – 0.6) m = 2.4 m
अब, समकोण त्रिभुज ∆ABD में,
पाइथागोरस प्रमेय से,
AD² = AB² + BD²
(2.4)² = (1.8)² + BD²
BD² = 5.76 – 3.24
BD² = 2.52 m
BD = 1.587 m.
∴ नाज़िमा द्वारा तय की गई क्षैतिज दूरी
= BD + 1.2 m
= (1.587 + 1.2)m
= 2.787 m
= 2.79 m
अब, डोरी की लंबाई और नाज़िमा द्वारा तय की गई दूरी 3m और 2.79 m

इस पोस्ट में आपको Class 10 maths chapter 6 exercise 6.6 triangles worksheet Class 10 maths chapter 6 exercise 6.6 triangles solutions Class 10 maths chapter 6 exercise 6.6 triangles questions class 10 triangles important questions with solutions pdf कक्षा 10 गणित अध्याय 6 त्रिभुज प्रश्नावली 6.6 एनसीईआरटी समाधान कक्षा 10 गणित अध्याय 6 त्रिभुज NCERT Solutions Class 10 त्रिभुज Ex 6.6 से संबंधित पूरी जानकारी दी गई है अगर इसके बारे में आपका कोई भी सवाल या सुझाव हो तो नीचे कमेंट करके हम से जरूर पूछें और अगर आपको यह जानकारी फायदेमंद लगे तो अपने दोस्तों के साथ शेयर जरूर करें.

NCERT Solutions for Class 10 Maths Chapter 6 त्रिभुज Exercise 6.1
NCERT Solutions for Class 10 Maths Chapter 6 त्रिभुज Exercise 6.2
NCERT Solutions for Class 10 Maths Chapter 6 त्रिभुज Exercise 6.3
NCERT Solutions for Class 10 Maths Chapter 6 त्रिभुज Exercise 6.4
NCERT Solutions for Class 10 Maths Chapter 6 त्रिभुज Exercise 6.5
NCERT Solutions for Class 10 Maths Chapter 6 त्रिभुज Exercise 6.6