Class 10 Maths Chapter 6 Exercise 6.5 – त्रिभुज

Class 10 Maths Chapter 6 Exercise 6.5 – त्रिभुज

NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.5 – आज हम आप के लिए Class 10 Maths Chapter 6 Triangles में लेकर आयें है। जो कि Class 10 Maths Exams के लिए अत्यन्त उपयोगी साबित होगी. कक्षा 10वीं के विद्यार्थी के लिए यहां पर एनसीईआरटी कक्षा 10 गणित अध्याय 6. (त्रिभुज) प्रश्नावली 6.5 के लिए सलूशन दिया गया है. जोकि एक सरल भाषा में दिया है .ताकि विद्यार्थी को पढने में कोई दिक्कत न आए .इसकी मदद से आप अपनी परीक्षा में अछे अंक प्राप्त कर सकते है.

NCERT Solutions For Class 10th Maths त्रिभुज (प्रश्नावली 6.5)

(i) 7 cm, 24 cm, 25 cm
(ii) 3 cm, 8 cm, 6 cm
(iii) 50 cm, 80 cm, 100 cm
(iv) 13 cm, 12 cm, 5 cm.

हल : (i) मान लीजिए ∆ABC में,

AB = 7 cm
BC = 24 cm, AC = 25 cm
AB² + BC² = (7)² + (24)²
= 49 + 576 = 625
AC² = (25)² = 625
अब AB² + BC² = AC²

∴ ∆ ABC एक समकोण त्रिभुज है।

(ii) मान लीजिए ∆PQR में,

PQ = 3 cm, QR = 8 cm
PR = 6 cm
PO² + PR² = (3)² + (6)²
= 9 + 36 = 45
QR² = (8)² = 64
यहाँ PQ² + PR² ≠ QR²

∴ ∆ PQR समकोण त्रिभुज नहीं है।

(iii) मान लीजिए ∆MNP में, MN = 50 cm,

NP = 80 cm, MP = 100 cm
MN² + NP² = (50)² + (80)²
= 2500 + 6400 = 8900
MP² = (100)² = 10000
यहाँ MP² ≠ MN² + NP²

∴ ∆MNP समकोण त्रिभुज नहीं है।

(iv) मान लीजिए ∆ABC में,

AB = 13 cm, BC = 12 cm,
AC = 5 cm
BC² + AC² = (12)² + (5)²
= 144 + 25 = 169
AB² = (13)² = 169
∴ AB² = BC² + AC²

∆ABC समकोण त्रिभुज है।

हल : दिया है : समकोण ∆PQR में कोण P समकोण है। Q पर बिंदु M इस प्रकार स्थित है कि PM ⊥ QR है।सिद्ध करना है : PM² = QM x MR

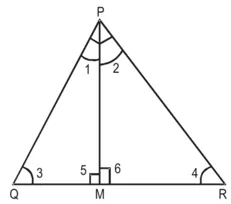
उपपत्ति: (दिया है)

∠P = 90°
∴ ∠1 + ∠2 = 90° …(1)
∠M = 90°
∆PMQ में,
∠1 + ∠3 + ∠n = 180° …(2)
∠1 + ∠3 = 90°
[∠M = 90°] (1) और (2) से,
∠1 + ∠2 = ∠1 + ∠3
∠2 = ∠3
∆QPM और ∆RPM में,
∠3 = ∠2 (प्रमाणित)
∠5 = ∠6 (प्रत्येक 90°)

∴ ∆QMP ~ ∆PMR [AA समरूपता]

क्षे०/क्षे०

[यदि दो त्रिभुजें समरूप हैं, तो उनके क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के वर्गों के अनुपात के बराबर होता है।]

[∵ त्रिभुज का क्षेत्रफल = आधार x शीर्षलम्ब]

PM² = QM x RM ] [अतः सत्यापित]

(i) AB² = BC.BD
(ii) AC² = BC.DC
(iii) AD² = BC.CD

हल : ∆DAB और ∆DCA में,

∠D = ∠D (उभयनिष्ठ)
∠A = ∠C (प्रत्येक 90°)
∴ ∆DAB ~ ∆DCA [AA समरूपता] ∆DAB और ∆ACB में, …(1)
∠B = ∠B (उभयनिष्ठ)
∠A = ∠C (प्रत्येक 90°)
∴ ∆DAB ~ ∆ACB ….(2)
(1) और (2) से,
∆DAB ~ ∆ACB ~ ∆DCA
(i) ∆ACB ~ ∆DAB (प्रमाणित)

∴ क्षे०/क्षे०

[यदि दो त्रिभुजें समरूप हैं, तो उनके क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के वर्गों के अनुपात के बराबर होता है।]

[∵ त्रिभुज का क्षेत्रफल = आधार x शीर्षलम्ब]

AB² = BC x BD

(ii) ∆ACB ~ ∆DCA (प्रमाणित)

क्षे०/क्षे०

[यदि दो त्रिभुजें समरूप हों, तो उनके क्षेत्रफलों का अनुपात संगत भुजाओं के अनुपात के वर्ग के

बराबर होता है।]

OB = 1800 km.

समकोण ∆AOB में,

AB² = AO² + OB²

AB² = (1500)² + (1800)²

AB = √2250000 + 3240000

= 15490000

AB = 300 √61 km.

∴ दोनों हवाई जहाज़ों के बीच की दूरी = 300 √61 km

[∵ त्रिभुज का क्षेत्रफल = आधार x शीर्षलम्ब

AC² = BC x DC

(iii) ∆DAB ~ ∆DCA (प्रमाणित)

क्षे०/क्षे०

[यदि दो त्रिभुजें समरूप हों, तो उनके क्षेत्रफलों का अनुपात संगत भुजाओं के अनुपात के वर्ग के बराबर होता है।]

⇒ AD² = BD x CD

हल : दिया है : ∆ABC एक समद्विबाहु त्रिभुज है जिसका कोण C समकोण है।

सिद्ध करना है : AB² = 2AC²

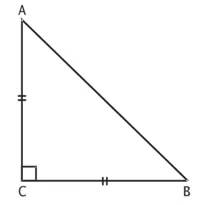
उपपत्ति : ∆ACB में, LC = 90°
AC = BC (दिया है)
AB² = AC² + BC²
[पाइथागोरस प्रमेय से] = AC² + AC² [BC = AC] AB² = 2AC² [अतः सत्यापित

हल : दिया है : ∆ABC एक समद्विबाहु त्रिभुज है जिसका कोण AC = BC है।

AB² = 2AC²
सिद्ध करना है : ∆ABC एक समकोण त्रिभुज है।

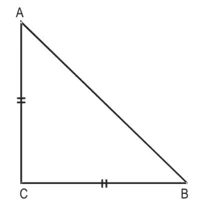
उपपत्ति : AB² = 2AC² (दिया है)
AB² = AC² + AC²
AB² = AC² + BC² [AC = BC]

∴ पाइथागोरस प्रमेय के विलोम से, ∆ABC समकोण त्रिभुज है।

हल : ∆ABC समबाहु त्रिभुज है जिसकी भुजा 2α है।

AD ⊥ BC
AB = AC = BC = 2α
∆ADB ≅ ∆ADC [RHS सर्वांगसमता से] ∴ BD = DC = α

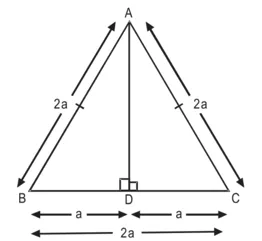
समकोण ∆ ADB में,
AB² = AD² + BD²
(2α)² = AD² + (α)²
4α² – α² = AD²
AD² = 3α²
AD² = 3α²
AD = √3α

हल : दिया है : समचतुर्भुज ABCD के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं।

सिद्ध करना है :

AB² + BC² + CD² + AD² = AC² + BD²

उपपत्ति : ∵ समचतुर्भुज के विकर्ण परस्पर समकोण पर समद्विभाजित होते हैं।

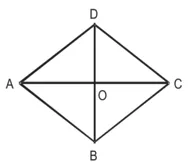
∴ AO = CO, BO = DO
∴ O पर कोण समकोण हैं

∆AOB में, ∠AOB = 90°
∴ AB² = AO² + BO² ….(1)

[पाइथागोरस प्रमेय से]

इसी प्रकार, BC² = CO² + BO² …(2)
CD² = CO² + DO² ….(3)
और DA² = DO² + AO² ….(4)

(1), (2), (3) और (4) को जोड़ने पर हमें प्राप्त होता है।

AB² + BC² + CD² + DA²
= 2AO² + 2CO² + 2BO² + 2DO²
= 4AO² + 4BO²
[∵ AO = CO और BO = DO] = (2AO)² + (2BO)² = AC² + BD²

(i) OA² + OB² + OC² – OD² – OE² – OF²
= AF² + BD² + CE²
(ii) AF² + BD² + CE²
= AE² + CD² + BF²

हल : दिया है : एक ∆ABC जिसमेंOD ⊥ BC, OE ⊥ AC और OF ⊥ AB है।

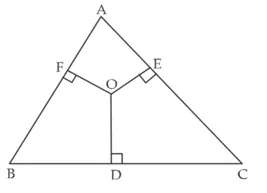
सिद्ध करना है :

(i) AF² + BD² + CE² = OA² + OB² + OC² – OD² – OE² – OF²

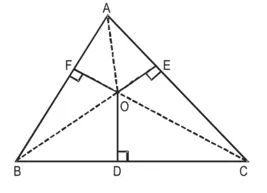
(ii) AF² + BD² + CE²
= AE² + CD² + BF²

रचना : AB, OC और OA को मिलाइए।

उपपत्ति : (i) समकोण ∠∆AFO में,
OA² = OF² + AF²

[पाइथागोरस प्रमेय से।]

या AF² = OA² – OF² …(1)
समकोण ∆BDO में,

OB² = BD² + OD² [पाइथागोरस प्रमेय से]

⇒ BD² = OB² – OD² ….(2)
समकोण ∆CEO में,

OC² = CE² + OE² [पाइथागोरस प्रमेय से]

⇒ CE² = OC² – OE² ….(3)
∴ AF² + CD² + CE²
= OA² – OF² + OB² – OD² + OC² – OE²

[(1), (2), और (3) को जोड़ने पर]

= OA² + OB² + OC² – OD²
– OE² – OF²

जोकि (1) को सिद्ध करता है।

पुन : AF² + BD² + CE²
= (OA² – OE²) + (OC² – OD²)
+ (OB² – OF²)
= AE² + CD² + BF²

{∵ AE² = AO² – OE²}
{CD² = OC² – OD²}
{BF² = OB² – OF²}

हल : खिड़की की धरती से ऊँचाई (AB) = 8m

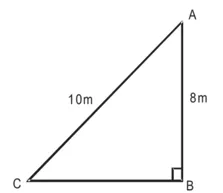
सीढ़ी की लंबाई (BC) = 10 m

सीढ़ी के निचले सिरे और दीवार के आधार के बीच की दूरी (BC) = ?

∆ABC में,
AB² + BC² = AC² [पाइथागोरस प्रमेय से] (8)² + (BC)² = (10)²
64 + BC² = 100
BC² = 100 – 64
BC = √36
BC = 6 cm

∴ सीढ़ी के निचले सिरे और दीवार के आधार के बीच की दूरी = 6 cm.

हल : मान लीजिए खंभे की ऊँचाई AB = 18 m

तार की लंबाई, BC = 24m

फोटो

C, खूटे की स्थिति है। इसकी खंभे के आधार से दूरी BC = है। समकोण ABC,

AB + BC² = AC² [पाइथागोरस प्रमेय से]

(18)² + (BC)² = (24)²
324 + (BC)² = 576
BC² = 576 – 324
BC = √252
BC = 6√7 m

= 100 km/hr.

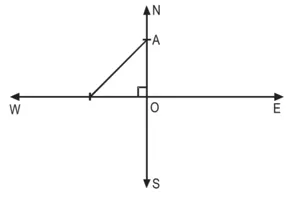
पहले हवाई जहाज़ द्वारा उत्तर की ओर घंटे में तय की गई दूरी

= OA = 1500

दूसरे हवाई जहाज़ की चाल

= 1200 km/hr.

दूसरे हवाई जहाज़ द्वारा घंटे में तय की गई दूरी

हल : खंभे की ऊँचाई, AB = 11m
खंभे की ऊँचाई (CD) = 6 m

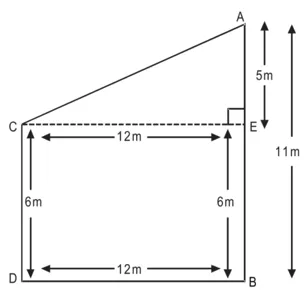
खंभों के आधारों में दूरी = 12 m
C से CE ⊥ AB खींचिए
BE = DC = 6m
AE = AB – BE
= (11 – 6) m = 5m

समकोण ∆AEC में,

AC² = AE² + EC²
AC = √(5)² + (12)²
= √25 + 24
= √169 = 13

∴ खंभों के ऊपरी सिरों के बीच की दूरी = 13m.

हल : दिया है : ∆ABC एक समकोण त्रिभुज है जिसमें C पर समकोण है भुजाओं CA और CB पर क्रमशः बिंदु D और E स्थित हैं।

अर्थात्

सिद्ध करना है :

AE² + BD² = AB² + DE²

उपपत्ति : समकोण ∆BCA में,

AB² = BC² + CA² …(1)

[पाइथागोरस प्रमेय से]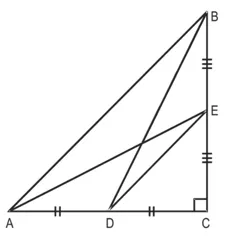

समकोण ∆ECD में,
DE² = EC² + DC² …..(2)

[पाइथागोरस प्रमेय से]

समकोण ∆ACE में,
AE² = AC² + CE² …..(3)
समकोण ∆BCD में,
BD² = BC² + CD² ….(4)

(3) और (4) को जोड़ने पर,

AE² + BD² = AC² + CE² + BC² + CD²
= [AC² + CB²] + [CE² + DC²] = AB² + DE² [(3) और (4) से] अतः, AE² + BD² = AB² + DE².

(देखिए आकृति)

सिद्ध कीजिए कि 2AB² = 2 AC² + BC² है।

हल : दिया है : ∆ABC में, AD ⊥ BC
BD = 3CD है।
सिद्ध करना है :
2AB² = 2AC² + BC²

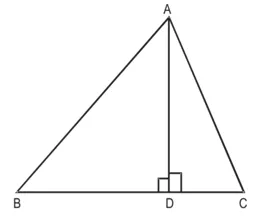
उपपत्ति :- समकोण त्रिभुजों ADB और ADC में,

AB² = AD² + BD²;
AC² = AD² + DC²

[पाइथागोरस प्रमेय से]

∴ AB² – AC² = BD² – DC²
= 9CD² – CD²;
[∵ BD = 3CD]

[∵ BC = DB + CD] [= 3 CD + CD] [= 4 CD]

⇒ 2(AB² – AC²) = BC²
⇒ 2AB² – 2AC² = BC²
∴ 2AB² = 2AC² + BC²

हल : दिया है : समबाहु त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि
सिद्ध करना है : 9AD² = 7AB²

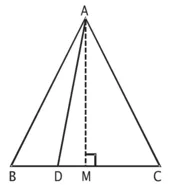
रचना : AB ⊥ BC

उपपत्ति :- ∆AMBO ≅ ∆AMC

[R.H.S. नियम से क्योंकि AM = AM और AB = AC]

पुन:

∴

और

(∵ BC, D पर तीन भागों में विभाजित है)

अब ∆ADC में, ∠C न्यून कोण है।

∴ AD² = AC² + DC² – 2DC x MC

और

[∵ AC = BC = AB]

∴

⇒ 9AD² = 7AB²

हल : दिया है : ∆ABC एक समबाहु ∆ है जिसमें

AB = BC = AC

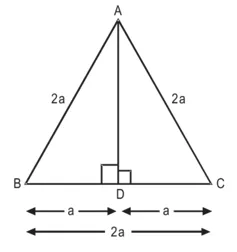
AD ⊥ DC
सिद्ध करना है : AB² = 4AD²
उपपत्ति : ∆ABC में,
मान लीजिए AB = BC = AC = 2α
AD ⊥ BC
∴
समकोण त्रिभुज में,
AB² = AD² + BD²
(2α)² = AD² + (α)²
4α² = AD² + α²
4α² – α² = AD²
AD² = 3α²

3AB²=4AB²

(a) 120° (b) 60°
(C) 90° (d) 45°

हल: AC = 12 cm

AB = 6√3 cm
BC = 6 cm
AC² = (12)² = 144 cm
AB² + BC² = (6√3)² + (6)²
= 108 + 36
AB² + BC² = 144
∴ AB² + BC² = AC²

पाइथागोरस प्रमेय के विलोम से,

∴ ∆ABC में B पर समकोण है .
∠B = 90°
∴ विकल्प (C) सही है।

इस पोस्ट में आपको Class 10 Maths Chapter 6 Exercise 6.5 Triangles class 10 maths chapter 6 pdf Class 10 maths chapter 6 exercise 6.5 triangles solutions NCERT Solutions for Class 10 Maths Chapter 6 Exercise 6.5 Class 10 Maths Chapter 6 Exercise 6.5 त्रिभुज ,कक्षा 10 गणित अध्याय 6 एनसीईआरटी समाधान त्रिभुज ,एनसीईआरटी समाधान कक्षा 10 गणित प्रश्नावली 6.5 NCERT Class-10 प्रश्नावली 6.5 Mathematics 6. त्रिभुज Class 10 maths chapter 6 triangles questions से संबंधित पूरी जानकारी दी गई है अगर इसके बारे में आपका कोई भी सवाल या सुझाव हो तो नीचे कमेंट करके हम से जरूर पूछें और अगर आपको यह जानकारी फायदेमंद लगे तो अपने दोस्तों के साथ शेयर जरूर करें.

NCERT Solutions for Class 10 Maths Chapter 6 त्रिभुज Exercise 6.1
NCERT Solutions for Class 10 Maths Chapter 6 त्रिभुज Exercise 6.2
NCERT Solutions for Class 10 Maths Chapter 6 त्रिभुज Exercise 6.3
NCERT Solutions for Class 10 Maths Chapter 6 त्रिभुज Exercise 6.4
NCERT Solutions for Class 10 Maths Chapter 6 त्रिभुज Exercise 6.5
NCERT Solutions for Class 10 Maths Chapter 6 त्रिभुज Exercise 6.6