Class 10 Maths Chapter 6 Exercise 6.4 – त्रिभुज

Class 10 Maths Chapter 6 Exercise 6.4 – त्रिभुज

NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.4 – जो विद्यार्थी 10वीं कक्षा में पढ़ रहे है उनके लिए यहां पर एनसीईआरटी कक्षा 10 गणित अध्याय 6. (त्रिभुज) प्रश्नावली 6.4 के लिए सलूशन दिया गया है. जोकि एक सरल भाषा में दिया है .ताकि विद्यार्थी को पढने में कोई दिक्कत न आए .इसकी मदद से आप अपनी परीक्षा में अछे अंक प्राप्त कर सकते है. इसलिए निचे आपको एनसीईआरटी समाधान कक्षा 10 गणित अध्याय 6 त्रिभुज प्रश्नावली 6.4 दिया गया है .

NCERT Solutions For Class 10th Maths त्रिभुज (प्रश्नावली 6.4)

हल : ∆ABC ~ ∆DEF, ∆ABC का क्षेत्रफल = 64cm2 और ∆DEF का क्षेत्रफल = 121 cm2 और EF = 15.4 cm है।

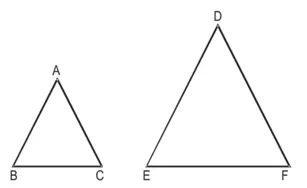
∆ABC ~ ∆DEF

∴ क्षे०(∆ABC)/क्षे०(∆DEF)

{यदि दो त्रिभुजें समरूप हों तो उनके क्षेत्रफलों का अनुपात संगत भुजाओं के अनुपात के वर्ग के बराबर होता है।}

⇒

BC = 8 x 1.4

BC = 11.2 cm.

हल : ABCD एक समलंब है जिसमें AB || DC है, के विकर्ण AC और BD परस्पर बिंदु O पर प्रतिच्छेद करते हैं। AB = 2CD है।

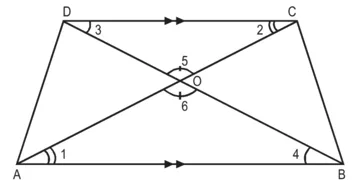
∆AOB और ∆COD में,
∠1 = ∠2 (एकांतर कोण)
∠3 = ∠4 (एकांतर कोण)
∠5 = ∠6 (शीर्षाभिमुख कोण)

∴ ∆AOB ~ ∆COD (AAA समरूपता कसौटी)

क्षे०./क्षे०.

{यदि दो त्रिभुजें समरूप हों, तो उनके क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के अनुपात का वर्ग होता है।

क्षे०./क्षे०.

∴ वांछित क्षे० ∆AOB

और क्षे० ∆COD का अनुपात = 4 : 1

क्षे०./क्षे०.

हल : दिया है : ∆ABC और ∆DBC एक ही आधार BC पर बने हुए हैं। AD, BC को O पर प्रतिच्छेद करती है।

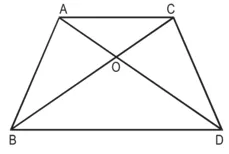
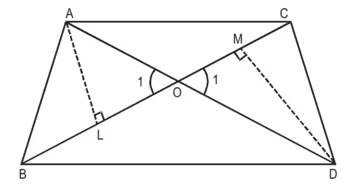
सिद्ध कीजिए : क्षे०./क्षे०.

रचना : AL ⊥ BC, DM ⊥ BC खींचिए।

उपपत्ति : ∆ALO और ∆DMO में,

∠1 = ∠2 (शीर्षाभिमुख कोण)

∠L = ∠M (प्रत्येक 90°)

∴ ∆ALO ~ ∆DMO

[AA समरूपता कसौटी]

∴ …(1)

[यदि दो त्रिभुजें समरूप हों, तो संगत भुजाएँ समानुपाती होती हैं।}

क्षे०/क्षे०

क्षे०/क्षे०

क्षे०/क्षे०

सिद्ध करना है : ∆ABC ≅ ∆DEF

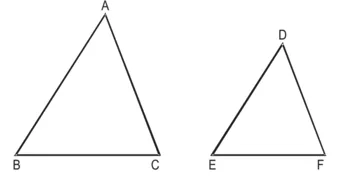
उपपत्ति : चूँकि ∆ABC ~ ∆DEF

क्षे०/क्षे०

⇒

[∵ क्षे० (∆ABC) = क्षे० (∆ABC)]

⇒ BC² = EF²

⇒ BC = EF

साथ ही, चूँकि ∆ABC ~ ∆DEF, इसलिए वे समकोणिक हैं
और ∠B = ∠E
और ∠C = ∠F
अब त्रिभुजों ABC और DEF में,
∠B = ∠E, ∠C = ∠F
और BC = EF
∴ ∆ABC ≅ ∆DEF
(ASA सर्वांगसमता प्रमेय)

हल:

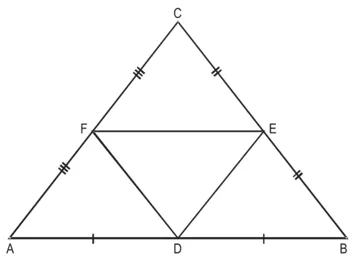
दिया है : एक AABC की भुजाओं AB, BC और CA के मध्य-बिंदु क्रमश: D, E और F हैं।
अभीष्ट : क्षे० (∆DEF) : क्षे० (∆ABC) ज्ञात करना।
उपपत्ति : ∆ABC में,

F, AC का मध्य-बिंदु है। ….(दिया है)

E, BC का मध्य-बिंदु है। …(दिया है)

इसलिए मध्य-बिंदु प्रमेय से,

FE || AB और

⇒ FE || AB

और FE = AD

∴ ADEF एक समांतर चतुर्भुज है

(∵ सम्मुख भुजाएँ समांतर और समान हैं।)

त्रिभुजों FAD और DEF में,

FA = DE

….(|| gm BDEF की सम्मुख भुजाएँ)

FD = FD …..(उभयनिष्ठ)

AD = FE

…..(|| gm BDEF की सम्मुख भुजाएँ)

∴ ∆FAD ≅ ∆DEF

….. (SSS सर्वांगसमता प्रयोग)

इसी प्रकार, हम सिद्ध कर सकते हैं कि

∆CFE ≅ ∆DEF

और ∆EDB ≅ ∆DEF

यदि त्रिभुजें सर्वांगसम हों, तो वे क्षेत्रफल में बराबर होती हैं।

क्षे० (∆FAD) = क्षे० (∆DEF) ….(1)

क्षे० (∆CFE) = क्षे० (∆DEF) ….(2)

क्षे० (∆EDB) = क्षे० (∆DEF) …..(3)

अब क्षे० ∆ (ABC)

= αr (∆FAD) + αr (∆DEF) + αr (∆CFE) + αr (∆EDB)

= αr (∆DEF) + αr (∆DEF) + αr (∆DEF) + αr (∆DEF)

[(1), (2) और (3) का प्रयोग करने पर]

= 4 क्षे० (∆DEF)

⇒ क्षे० क्षे० (∆ABC)

⇒ क्षे०/क्षे०

∴ क्षे० (∆DEF) : क्षे० (∆ABC) = 1 : 4

 

∆ABC ~ ∆DEE.

AX और DY क्रमशः भुजाओं BC और EF की माध्यिकाएँ हैं।

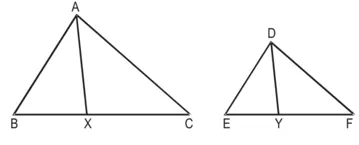
सिद्ध करना है :

उपपत्ति : ∆ABC ~ ∆DEF (दिया है)

∴

[∵ AX और DY माध्यिकाएँ हैं

∴ BC = 2BX और EF = 2EY]

⇒ ….(1)

∆ABX और ∆DEY में,

∠B = ∠E [∵ ∆ABC ~ ∆DEF]

[(1) में सिद्ध किया है]

∴ ∆ABC ~ ∆DEY

[SAS समरूपता कसौटी]

∴ …(2)

चूंकि, दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात इनकी संगत भुजाओं के अनुपात के वर्ग के बराबर होता है।

∴ क्षे०/क्षे० [अतः सत्यापित

हल : दिया है : ABCD एक वर्ग है।

समबाहु ∆ABC वर्ग की भुजा AB पर स्थित है और समबाहु ∆ACF विकर्ण AC पर बनी है।

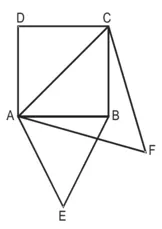
सिद्ध करना है : क्षे०/क्षे०

उपपत्ति : समकोण ∆ABC में,

AB² + BC² = AC²

[पाइथागोरस प्रमेय द्वारा]

⇒ AB² + AB² = AC²

[∵ AB = BC, एक ही वर्ग की भुजाएँ]

⇒ 2AB² = AC² …(1)

अब, प्रत्येक ∆ABC और ∆ACF समबाहु और इसलिए समकोणिक हैं और इसलिए समरूप हैं।

अर्थात् ∆ABE ~ ∆ACF

यहाँ पहली ∆ की कोई भुजा दूसरी त्रिभुज की किसी भुजा से समांतर है।

∴ क्षे०/क्षे०

[∵ दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के अनुपात के वर्ग के बराबर होता है।]

[(1) का प्रयोग करने पर]

सही उत्तर चुनिए और अपने उत्तर का औचित्य दीजिए:

(a) 2 : 1 (b) 1 : 2
(c) 4 : 1 (d) 1 : 4

हल : ∆ABC और ∆BDE दो समबाहु त्रिभुज इस प्रकार है कि D भुजा BC का मध्य बिन्दु है।

∴
मान लीजिए समबाहु त्रिभुज की भुजा 2a है।

∴ ∆ABC ~ ∆BDE

∴ क्षे०/क्षे०

∴ (c) सही विकल्प है

(a) 2 : 3 (b) 4 : 9
(c) 81 : 16 (d) 16 : 81
हल:

∆ABC ~ ∆DEF (दिया है)

∴ क्षे०/क्षे०

[दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के अनुपात के वर्ग के बराबर होता है]

∴ क्षे०/क्षे०

(d) सही विकल्प है।

इस पोस्ट में आपको Class 10 maths chapter 6 exercise 6.4 triangles solutions Class 10 maths chapter 6 exercise 6.4 triangles question answer class 10 ncert solutions exercise 6.4 Class 10 Maths Chapter 6 Exercise 6.4 Triangles Class 10 Maths Chapter 6 Triangles Ex 6.4 questions with solutions कक्षा 10 एनसीईआरटी पुस्तक समाधान प्रश्नावली 6.4 कक्षा 10 गणित अध्याय 6 एनसीईआरटी समाधान त्रिभुज कक्षा 10 गणित अध्याय 6 त्रिभुज प्रश्नावली 6.4 से संबंधित पूरी जानकारी दी गई है अगर इसके बारे में आपका कोई भी सवाल या सुझाव हो तो नीचे कमेंट करके हम से जरूर पूछें और अगर आपको यह जानकारी फायदेमंद लगे तो अपने दोस्तों के साथ शेयर जरूर करें.

NCERT Solutions for Class 10 Maths Chapter 6 त्रिभुज Exercise 6.1
NCERT Solutions for Class 10 Maths Chapter 6 त्रिभुज Exercise 6.2
NCERT Solutions for Class 10 Maths Chapter 6 त्रिभुज Exercise 6.3
NCERT Solutions for Class 10 Maths Chapter 6 त्रिभुज Exercise 6.4
NCERT Solutions for Class 10 Maths Chapter 6 त्रिभुज Exercise 6.5
NCERT Solutions for Class 10 Maths Chapter 6 त्रिभुज Exercise 6.6