Class 10 Maths Chapter 5 Exercise 5.3 – समांतर श्रेढी
NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progression Ex 5.3 – हर विद्यार्थी का सपना होता है कि वे अपनी कक्षा में अच्छे अंक से पास हो ,ताकि उन्हें आगे एडमिशन या किसी नौकरी के लिए फॉर्म अप्लाई करने में कोई दिक्कत न आए . कक्षा 10वीं के विद्यार्थी के लिए यहां पर एनसीईआरटी कक्षा 10 गणित अध्याय 5. (समांतर श्रेढी) प्रश्नावली 5.3 के लिए सलूशन दिया गया है. जोकि एक सरल भाषा में दिया है .ताकि विद्यार्थी को पढने में कोई दिक्कत न आए .इसकी मदद से आप अपनी परीक्षा में अछे अंक प्राप्त कर सकते है.
NCERT Solutions For Class 10th Maths समांतर श्रेढी (प्रश्नावली 5.3)
(i) 2, 7, 12, … 10 पदों तक।
(ii) – 37, – 33, – 29,… 12 पदों तक।
(iii) 0.6, 1.7, 2.8, … 100 पदों तक।
(iv) ![]() पदों तक।
पदों तक।
यहां α = 2, d = 7 – 2 = 5
और n = 10
सूत्र ![]() के प्रयोग से,
के प्रयोग से,
![]()
= 5 [4 + 45] = 245
(ii) दी गई A.P. है : – 37, – 33, – 29…यहां α = – 37, d = – 33 + 37 = 4
और n = 12
सूत्र ![]() के प्रयोग से,
के प्रयोग से,
![]()
= 6 [- 74 + 44] = – 180 उत्तर
(iii) दी गई A.P. है : 0.6, 1.7, 2.8,….यहां α = 0.6, d = 1.7 – 0.6 = 1.1
और n = 100
सूत्र ![]() के प्रयोग से,
के प्रयोग से,
![]()
= 50 [1.2 + 108.9] = 5505 उत्तर
(iv) दी गई A.P. है :
![]()
यहां ![]()
![]()
![]()
और n = 11
सूत्र ![]() के प्रयोग से,
के प्रयोग से,
![]()
![]()
![]() उत्तर
उत्तर
(i) ![]()
(ii) 34 + 32 + 30 + … + 10
(iii) – 5 + (- 8) + (- 11) + … + (- 230)
![]()
यहाँ ![]()
![]()
और l = Tn = 84
या α + (n – 1) d = 84
या ![]()
या ![]()
या ![]()
या n = 22 + 1 = 23
अब, ![]()
![]()
![]() उत्तर
उत्तर
(ii) दी गई A.P. है :
34 + 32 + 30 + … + 10
यहां α = 34, d = 32 – 34 = – 2
और l = Tn = 10
α + (n – 1) d = 10
या 34 + (n -1) ( -2) = 10
या – 2 (n -1) = 10 – 34 = – 24
या ![]()
या n = 12 + 1 = 13
अब, ![]()
![]()
![]() उत्तर
उत्तर
– 5 + (- 8) + (- 11) + … + (- 230)
यहाँ α = – 5, d = – 8 + 5 = – 3
और l = Tn, = – 230
α + (n -1) d = – 230
या – 5 + (n – 1) (-3) = – 230
या – 3 (n -1) = – 230 + 5 = – 225
या ![]()
या n = 75 + 1 = 76
अब, ![]()
![]()
= 38 (- 235)
= – 8930 उत्तर
(i) a = 5, d = 3, an = 50 दिया है। n और Sn ज्ञात कीजिए।
(ii) a = 7, a13 = 35 दिया है। d और S13 ज्ञात कीजिए।
(iii) a12 = 37, d = 3 दिया है। a और S12 ज्ञात कीजिए।
(iv) a3 = 15, S10 = 125 दिया है। d और a10 ज्ञात कीजिए।
(v) d = 5, S9 = 75, दिया है। a और a9 ज्ञात कीजिए।
(vi) a = 2, d = 8, Sn = 90 दिया है। n और an ज्ञात कीजिए।
(vii) a = 8, an = 62. Sn = 210 दिया है। n और d ज्ञात कीजिए।
(viii) an = 4, d = 2, Sn = – 14 दिया है। n और a ज्ञात कीजिए।
(ix) a = 3, n = 8, S = 192 दिया है। d ज्ञात कीजिए।
(x) I = 28, S = 144 दिया है। और कुल पद 9 हैं। a, ज्ञात कीजिए।
∵ αn = 50
α + (n – 1) d = 50
या 5 + (n – 1) 3 = 50
या 3 (n – 1) = 50 – 5 = 45
या ![]()
या n = 15 + 1 = 16
अब, ![]()
![]()
= 440 उत्तर
(ii) दिया है α = 7, α13 = 35∵ α13 = 35
α + (n – 1) d = 35
या 7 + (13 -1) d = 35
या 12 d = 35 – 7 = 28
या ![]()
अब, ![]()
![]()
![]()
= 273
(iii) दिया है α12 = 37, d = 3∵ α12 = 37
α + (n – 1) d = 37
या α + (12 -1) 3 = 37
α = 37 – 33 = 4
α = 37 – 33 = 4
अब, ![]()
![]()
= 6 x 41 = 246
(iv) दिया है α3 = 15, S10 = 125∵ α3 = 15
α + (n – 1) d = 15
या α + (3 – 1) d = 15
या α + 2d = 15 ….(1)
∵ S10 = 125
![]()
![]()
या 5[2α + 9d] = 125
या ![]()
या 2α + 9d = 25 ….(2)
(1) से α = 15 – 2d ….(3)
α का मान (2), में प्रतिस्थापित करने पर हमें प्राप्त होता है :
2(15 – 2d) + 9d = 25
या 30 – 4 d + 9d = 25
या 5d = 25 – 30
d का मान (3) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
α = 15 – 2 (-1)
α = 15 + 2 = 17
अब, α10 = 17 + (10 – 1) (- 1)
|∵ αn = α + (n – 1) d
= 17 – 9 = 8
∵ S9 = 75
या ![]()
![]()
या ![]()
या ![]()
या ![]()
या ![]()
या ![]()
अब, α9 = α + (n – 1)d
![]()
![]()
![]() उत्तर
उत्तर
Sn = 90
![]()
या ![]()
या n [2 + 4n – 4] = 90
या n (4n – 2) = 90
या 4n2 – 2n – 90 = 0
या 2n2 – n – 45 = 0
या 2n2 – 10n + 9n – 45 = 0
[∵ S = – 2
P = – 45 x 2 = – 90]
या 2n [n – 5] + 9 (n – 5) = 0
या (2n + 9) (n – 5) = 0
अर्थात् 2n + 9 = 0
या n – 5 = 0![]() अर्थात् n = 5
अर्थात् n = 5
∵ n ऋणात्मक नहीं हो सकता इसलिए ![]() को छोड़ दीजिए।
को छोड़ दीजिए।
∴ n = 5
अब, αn = α5 = α + (n – 1) d
= 2 + (5 – 1) 8
= 2 + 32 = 34
∵ Sn, = 210
![]()
या ![]()
या ![]()
या ![]()
अब αn = 62
8 + (6 – 1) d = 62 |∵ Tn = α + (n – 1) d
या 5d = 62 – 8 = 54
या ![]()
∵ αn = 4
α + (n – 1) d = 4
या α + (n – 1) 2 = 4
या α + 2n – 2 = 4
या α = 6 – 2n …..(1)
और Sn = – 14
![]()
या ![]() [(1) के प्रयोग से]
[(1) के प्रयोग से]
या ![]()
या 5n – n2 – 14 = 0
या n2 – 5n – 14 = 0 S = – 5
या n2 – 7n + 2n – 14 = 0 P = 1 x – 14
या n2 – 7n + 2n – 14 = 0 = – 14
या n(n – 7) + 2 (n – 7) = 0
या (n – 7) (n + 2) = 0
अर्थात् n – 7 = 0 या n + 2 = 0
n = 7 या n = – 2
∵ n ऋणात्मक नहीं हो सकता।
∵ n = – 2 को छोड़ दीजिए।
∴ n = 7
n का मान (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
α = 6 – 2 x 7
α = 6 – 14 = – 8
∵ S = 192
⇒ S8 = 192 [∵ n = 8]
या ![]()
![]()
या 4 [6 + 7d] = 192
या ![]()
या 7d = 48 – 6 = 42
या ![]()
∴ n = 9; 1 = α9 = 28 ; S9 = 144
∵ α9 = 28
या α + (9 – 1)d = 28 |∵ αn = Tn = 9 + (n – 1)d …(1)
या α + 8d = 28
और S9 = 144
![]()
![]()
या ![]()
α = 32 – 28 = 4
9, 17, 25, …
यहां α = 9, d = 17 – 9 = 8 क्योंकि
Sn= 636
![]()
या ![]()
या ![]()
या n[4n+5]=636
या 4n2 + 5n – 636 = 0
α = 4,b = 5, c = – 636
D = (5)2 – 4 x 4 x (-636)
= 25 + 10176
= 10201
∴ ![]()
![]()
![]() या
या ![]() या 12.
या 12.
∵ n ऋणात्मक नहीं हो सकता।
अंत: ![]() को छोड़ दीजिए
को छोड़ दीजिए
∴ n = 12
अंतः दी गई A.P. के 12 पदों का योग 636 है। उत्तर
और Sn = 400
∵ Tn = 45
α + (n – 1)d = 45
या 5 + (n – 1) d = 45
या (n – 1) d = 45 – 5 = 40
या (n – 1) d = 40 …(1)
और Sn = 400
![]()
![]()
या 25n=400
या ![]()
n का मान (1), में प्रतिस्थापित करने पर, हमें प्राप्त होता है :
(16 – 1) d = 40
या 15d = 40
या ![]()
अतः, n = 16 और ![]() उत्तर
उत्तर
l = αn = 350
और d = 9
∵ l = αn = 350
α + (n – 1) d = 350
17 + (n – 1) 9 = 350
या 9(n – 1) = 350 – 17 = 333
या ![]()
या n = 37 + 1 = 38
अब, ![]()
![]()
= 19 x 367 = 6973
अतः दी गई A.P. के 38 पदों का योग 6973 है। उत्तर
और n = 22
∴ T22 = 149
α + (n – 1) d = 149
या α + (22 – 1) 7 = 149
या α + 147 = 149
या α = 149 – 147 = 2
अब, ![]()
![]()
= 11 x 151 = 1661
अतः, दी गई A.P. के प्रथम 22 पदों का योग 1661 है। उत्तर
दिया गया है कि T2 = 14; T3 = 18
और n = 51
∵ T2 = 14
α + (n – 1) d = 14
α + (2 – 1) d = 14
या α + d = 14
या α = 14 – d …..(1)
और T3 = 18 (दिया है)
α + (n – 1) d = 18
α + (3 – 1) d = 18
या α + 2d = 18
या 14 – d + 2d = 18
या d = 18 – 14 = 4
या d = 4
d का मान (1), में प्रतिस्थापित करने पर, हमें प्राप्त होता है :
α = 14 – 4 = 10
अब, ![]()
![]()
![]()
![]()
अतः, दी गई A.P. के प्रथम 51 पदों का योग 5610 है। उत्तर
S7 = 49
![]()
या ![]()
या ![]()
या α + 3d = 7
या α = 7 – 3d …..(1)
दूसरी शर्त के अनुसार,
S17 = 289
![]()
![]()
![]()
α का मान (1), में प्रतिस्थापित करने पर हमें प्राप्त होता है :
7 – 3d + 8d = 17
5d = 17 – 7 = 10![]()
d का मान (1), में प्रतिस्थापित करने पर हमें प्राप्त होता है :
α = 7 – 3 x 2
α = 7 – 6 = 1
अब, ![]()
![]()
= n[1 x n + 1 = n x n
= n 2
अतः, दी गई A.P. के प्रथम n पदों का योग n 2 है। उत्तर
(i) an = 3 + 4n
(ii) an = 9 – 5n
साथ ही, प्रत्येक स्थिति में, प्रथम 15 पदों का योग ज्ञात कीजिए।
n के विभिन्न मान (1), में प्रतिस्थापित करने पर,
α1 = 3 + 4 (1) = 7;
α2 = 3 + 4 (2) = 11
α1 = 3 + 4 (3) = 15, …
अब α2 – α1, α3 – α2 = 15 – 11 = 4
∵ α2 – α1 = 11 – 7 = 4
और α3 – α2 = 4 = d (मान लीजिए)
∴ दिया गया अनुक्रम A.P. का ही रूप है।
यहाँ α = 7, d = 4 और n = 15
∴ ![]()
![]()
![]()
= 15 x 35 = 525
n के विभिन्न मान (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
α1 = 9 – 5(1) = 4 ;
α2 = 9 – 5(2) = – 1;
α3 = 9 – 5(3) = – 6
अब, α2 – α1, = – 1 – 4 = – 5
और α3 – α2 = – 6 + 1 = – 5
∵ α2 – α1 = α3 – α2 = – 5 = d
(मान लीजिए)
∴ दिया गया अनुक्रम A.P. का ही रूप है।
यहाँ α = 4, d = – 5 और n = 15
∴ ![]()
![]()
![]()
= – 465
Sn = 4n – n2 …..(1)
n = 1 (1), में प्रतिस्थापित करने पर हमें प्राप्त होता है
S1 = 4(1) – (1)2 = 4 – 1
S1 = 3
∴ α = T1 = S1 = 3
n = 2, (1), में प्रतिस्थापित करने पर हमें प्राप्त होता है :
S2 = 4(2) – (2)2 = 8 – 4
S2 = 4
या T1 + T2 = 4
या 3 + T2 = 4
या T2 = 4 – 3 = 1
n = 3, (1), में प्रतिस्थापित करने पर हमें प्राप्त होता है :
S3 = 4 (3) – (3)2 = 12 – 9
S3 = 3
या S2 + T3 = 3 [∵ S3 = S2 + T3]
या 4 + T3 = 3
या T3 = 3 – 4 = – 1
अब, d = T2 – T1
= 1 – 3 = – 2
T10 = α + (n – 1) d
= 3 (10 – 1) (- 2)
T10 = 3 – 18 = – 15
और Tn, = α + (n – 1) d
= 3 + (n – 1) (- 2)
= 3 – 2n + 2
Tn = 5 – 2n
6, 12, 18, 24, 30, 36 42, …
यहाँ α = T1 = 6, T2 = 12,
T3 = 18, T4 = 24
d = T2 – T1 = 12 – 6 = 6
सूत्र ![]() का प्रयोग करने पर,
का प्रयोग करने पर,
![]()
= 20 [12 + 234] = 20 (246) = 4920
अतः, 6 से विभाज्य प्रथम 40 घन पूर्णांकों का योग 4920 है। उत्तर
यहाँ α = T1 = 8 ; T2 = 16 ;
d = T2 – T1 = 16 – 8 = 8
सूत्र ![]() का प्रयोग करने पर,
का प्रयोग करने पर,
![]()
![]()
![]()
अतः, 8 के प्रथम 15 गुणजों का योग 960 है। उत्तर
1, 3, 5, 7, 9, …, 49
यहाँ α = T1 = 1 ; T2 = 3 ;
और l = Tn = 49
d = T2 – T1 = 3 – 1 = 2
साथ ही l = Tn, = 49
α + (n – 1) = 49
1 + (n – 1) 2 = 49
या 2(n – 1) = 49 – 1 = 48
या ![]()
या n = 24 + 1 = 25
सूत्र ![]() का प्रयोग करने पर,
का प्रयोग करने पर,
![]()
![]()
![]()
अतः, 0 और 50 के बीच की विषम संख्याओं का योग 625 है। उत्तर
पहले दिन के लिए ₹ 200 दूसरे दिन के लिए ₹ 250, तीसरे दिने के लिए ₹ 300 इत्यादि, अर्थात् प्रत्येक उत्तरोत्तर दिन का जुर्माना अपने से ठीक पहले दिन के जुर्माने से ₹ 50 अधिक है। एक ठेकेदार को जुर्माने के रूप में कितनी राशि अदा करनी पड़ेगी, यदि वह इस कार्य में 30 दिन का विलंब कर देता है?
हल : पहले, दूसरे और तीसरे दिन के विलंब के लिए जुर्माना है : ₹ 200, ₹ 250, ₹ 300अब, जुर्माना अगले दिन ₹ 50 के अंतर से बढ़ता जाता है∴ अभीष्ट A.P. है : 200, 250, 300, 350, …
यहाँ α = T1 = 200 ; d = 50 और n = 30
30 दिन के पश्चात् दी जाने वाली जुर्माने की राशि
= S30
![]()
![]()
= 15 [400 + 1450]
= 15 (1850) = 27750
अतः, यदि ठेकेदार कार्य में 30 दिन विलंब करता है, तो उसे जुर्माने के रूप में ₹ 27,750 देने होंगे। उत्तर
दूसरे विद्यार्थी को दी गई पुरस्कार की राशि = ₹ (???? – 20)
तीसरे विद्यार्थी को दी गई पुरस्कार की राशि = ₹ [???? – 20 – 20]
= ₹ (???? – 40)
∴ अभीष्ट अनुक्रम है :
????, (???? – 20), (???? – 40), …
जो कि एक A.P. बनाती है, जिसमें
α = x d = – 20 और n = 7
सूत्र ![]() का प्रयोग करने पर,
का प्रयोग करने पर,
प्रश्न के अनुसार,
7(???? – 60) = 700
![]()
x = 100 + 60
x = 160
अतः, 7 पुरस्कार हैं : ₹ 160, ₹ 140, ₹ 120, ₹ 100, ₹ 80, ₹ 60, ₹ 40 उत्तर
कक्षा II के तीन अनुभागों द्वारा लगाए गए पेड़ों की संख्या = 3 x 2 = 6
कक्षा III के तीन भागों द्वारा लगाए गए पेड़ों की संख्या = 3 x 3 = 9
कक्षा XII के तीन अनुभागों द्वारा लगाए गए पेड़ों की संख्या = 3 x 12 = 36
∴ अभीष्ट A.P. है : 3, 6, 9,…, 36
यहाँ, α = T1 = 3 ; T2 = 6; T3 = 9
और l = Tn, = 36 ; n = 12
d = T2 – T1 = 6 – 3 = 3
विद्यार्थियों द्वारा लगाए गए पेड़ों की कुल संख्या = S12
विद्यार्थियों द्वारा लगाए गए पेड़ ![]()
![]()
अतः, वायु प्रदूषण को रोकने के लिए विद्यार्थियों द्वारा 234 पेड़ लगाए
जाएँगे। उत्तर
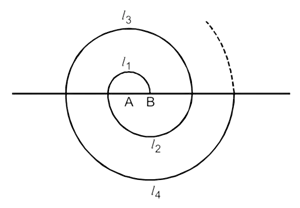
( लीजिए ![]() ) [संकेत : क्रमश: केंद्रों A, B, A, B,… वाले अर्धवृत्तों के परिमाप l1, l2, l3, l4, हैं।
) [संकेत : क्रमश: केंद्रों A, B, A, B,… वाले अर्धवृत्तों के परिमाप l1, l2, l3, l4, हैं।
![]()
l2 = दूसरे अर्धवृत्त का परिमाप
= ????r2 = ????(1) = ????
l3 तीसरे अर्धवृत्त का परिमाप
![]()
और l4 = चौथे अर्धवृत्त का परिमाप
= ????r4 = ????(2) = 2???? इसी तरह आगे भी
∵ उत्तरोत्तर अर्धवृत्तों के परिमाप एक A.P. बनाते हैं।
यहाँ ![]()
![]() और n = 13
और n = 13
![]()
![]()
सर्पिल की कुल लंबाई = S13
![]()
![]()
![]()
![]()
अतः, तेरह क्रमागत अर्धवृत्तों से बने सर्पिल की कुल लंबाई 143 cm है। उत्तर
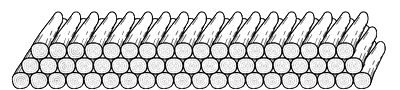
तीसरी पंक्ति में लट्ठों की संख्या = 18
इसी प्रकार आगे भी
∴ प्रत्येक पंक्ति में रखे गए लट्ठों की संख्या एक A.P. बनाती है।
यहाँ α = T1 = 20 ;
T2 = 19 ; T3 = 18…
d = T2 – T1
= 19 – 20 = – 1
मान लीजिए Sn लट्ठों की कुल संख्या को व्यक्त करता है। सूत्र का प्रयोग करने पर,![]()
∴ ![]()
![]()
![]()
प्रश्न के अनुसार,
![]()
या 41n2 – n2 = 400
या – n2 + 41n – 400 = 0
या n2 – 41n + 400 = 0 |S = – 41
या n2 – 16n – 25n + 400 = 0 |P = 400
या n (n – 16) – 25 (n – 16) = 0
या (n – 16) (n – 25) = 0
अर्थात् n – 16 = 0 या n – 25 = 0
अथवा n = 16 या n = 25
∴ n = 16, 25.
स्थिति I. जब n = 25
T25 = α + (n – 1) d
= 20 + (25 – 1) (- 1)
= 20 – 24 = – 4 ; जोकि असंभव है
∴ n = 25 छोड़ देते हैं
स्थिति II. जब n = 16
T16 = α + (n – 1) d
= 20 + (16 – 1) (- 1)
= 20 – 15 = 5
अतः, कुल 16 पंक्तियाँ हैं और सबसे ऊपरी पंक्ति में 5 लट्ठे हैं। उत्तर

प्रत्येक प्रतियोगी बाल्टी से चलना प्रारंभ करती है, निकटतम आलू को उठाती है, उसे उठाकर वापस आकर दौड़कर बाल्टी में डालती है, दूसरा आलू उठाने के लिए वापस दौड़ती है, उसे उठाकर वापस आकर बाल्टी में डालती है, और वह ऐसा तब तक करती रहती है, जब तक सभी आलू बाल्टी में न आ जाएँ। इसमें प्रतियोगी को कुल कितनी दूरी दौड़नी पड़ेगी.
[संकेत : पहले और दूसरे आलुओं को उठाकर बाल्टी में डालने तक दौड़ी गई दूरी = 2 x 5 + 2 x (5 + 3) है।]हल : पहला आलू उठाने के लिए तय की गई दूरी= 2(5) m = 10 m
उतरोत्तर आलुओं के बीच की दूरी = 3 m
∴ दूसरा आलू उठाने के लिए तय की गई दूरी
= 2 (5 + 3) m = 16 m
तीसरा आलू उठाने के लिए तय की गई दूरी
= 2 (5 + 3 + 3) m
= 22 m
और यह प्रक्रिया चलती रहती है। इससे स्पष्ट है कि यह स्थिति एक A.P. बन जाती है।
10, 16, 22, 22, 28, …
यहाँ α = T1 = 10; T2 = 16; T3 = 22, …
d = T2 – T1 = 16 – 10 = 6
और n = 10
∴ प्रतियोगी को कुल जितनी दूरी दौड़नी पड़ेगी समांतर श्रेढ़ी
= S10
![]()
![]()
= 5[20 + 54] 5 x 74 = 370
अतः, प्रतियोगी को कुल 370 m की दूरी दौड़नी पड़ेगी। उत्तर
इस पोस्ट में आपको class 10 maths exercise 5.3 solutions , class 10 maths chapter 5 solutions pdf download in hindi Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.3 Class 10 Maths समांतर श्रेढ़ियाँ Ex 5.3 Class 10 Maths Solutions Chapter 5 समांतर श्रेढ़ियाँ Ex 5.3 एनसीईआरटी समाधान कक्षा 10 गणित प्रश्नावली 5.3 से संबंधित पूरी जानकारी दी गई है अगर इसके बारे में आपका कोई भी सवाल या सुझाव हो तो नीचे कमेंट करके हम से जरूर पूछें और अगर आपको यह जानकारी फायदेमंद लगे तो अपने दोस्तों के साथ शेयर जरूर करें.
NCERT Solutions for Class 10 Maths Chapter 5 समांतर श्रेढ़ी Exercise 5.1
NCERT Solutions for Class 10 Maths Chapter 5 समांतर श्रेढ़ी Exercise 5.2
NCERT Solutions for Class 10 Maths Chapter 5 समांतर श्रेढ़ी Exercise 5.3
NCERT Solutions for Class 10 Maths Chapter 5 समांतर श्रेढ़ी Exercise 5.4