Class 10 Maths Chapter 3 Exercise 3.7 – दो चर वाले रैखिक समीकरण युग्म
कक्षा 10वीं के विद्यार्थी के लिए यहां पर एनसीईआरटी कक्षा 10 गणित अध्याय 3. (दो चर वाले रैखिक समीकरण युग्म ) प्रश्नावली 3.7 के लिए सलूशन दिया गया है. जोकि एक सरल भाषा में दिया है .ताकि विद्यार्थी को पढने में कोई दिक्कत न आए .इसकी मदद से आप अपनी परीक्षा में अछे अंक प्राप्त कर सकते है.
Class 10th Maths दो चर वाले रैखिक समीकरण युग्म (प्रश्नावली 3.7)
[su_note]प्रश्न 1. दो मित्रों अनी और बीजू की आयु में 3 वर्ष का अंतर है। अनी के पिता धर्म की आयु अनी की आयु से दुगुनी है और बीजू की आयु उसकी बहन कैथी की आयु से दुगुनी है। कैथी और धर्म की आयु में 30 वर्ष का अंतर है। अनी और बीजू की आयु ज्ञात कीजिए :[/su_note]
[su_label]हल : मान लीजिए,[/su_label]
अनी की आयु = ???? वर्ष
और बीजू की आयु = y वर्ष
धर्म की आयु = 2???? वर्ष
कैथी की आयु = 
वर्ष
पहली शर्त अनुसार,
– (अनी की आयु) – (बीजू का आयु) = 3
???? – y = 3 …..(1)
दूसरी शर्त अनुसार
(धर्म की आयु) – (कैथी की आयु) = 30
या 
या 4???? – y = 60
अब, (2) – (1) से प्राप्त होता है :
4???? – y = 60
???? – y = 3
– + –
3???? = 57
या 
???? के इस मान को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
19 – y = 3
या – y = 3 – 19
याया – y = – 16
या y = 16
अतः, अनी की आयु = 19 वर्ष
बीजू की आयु = 16 वर्ष
[su_note]प्रश्न 2. एक कहता है, “मित्र, मुझे सौ दे दो! मैं तब आपसे दुगुना अमीर बन जाऊँगा।” दूसरे ने उत्तर दिया, “यदि आप मुझे दस दे दो तो मैं आपसे छः गुना अमीर हो जाऊँगा।” बताइए प्रत्येक के पास कितनी पूँजी है ? [भाष्कर II के बीज गणित से] [संकेत : ???? + 100 = 2 (y – 100), y + 10 = 6 (x – 10)][/su_note]
[su_label]हल : मान लीजिए एक मित्र की पूँजी = ₹ ????[/su_label]
दूसरे मित्र की पूँजी = ₹ y
पहली शर्त अनुसार,
???? + 100 = 2 (y – 100)
या ???? + 100 = 2y – 200
या ???? – 2y = – 200 – 100
या ???? – 2y = – 300 ….(1)
दूसरी शर्त अनुसार
y + 10 = 6 (???? – 10)
या y + 10 = 6???? – 60
या 6???? – y = 10 + 60
या 6x – y = 70 ….(2)
(1) को 6 से गुणा करने पर हमें प्राप्त होता है:
6???? – 12y = – 1800
अब, (3) – (2) से प्राप्त होता है
6???? – 12y = – 1800
6???? – y = 70
– 11y = – 1870
y को (2) से गुणा करने पर हमें प्राप्त होता है:
6???? – 170 = 70
6???? = 70 + 170
या 6???? = 240
या 
अतः, उनकी पूँजी क्रमशः ₹ 40
और ₹ 170 है।
[su_note]प्रश्न 2. एक कहता है, “मित्र, मुझे सौ दे दो! मैं तब आपसे दुगुना अमीर बन जाऊँगा।” दूसरे ने उत्तर दिया, “यदि आप मुझे दस दे दो तो मैं आपसे छः गुना अमीर हो जाऊँगा।” बताइए प्रत्येक के पास कितनी पूँजी है ? [भाष्कर II के बीज गणित से] [संकेत : ???? + 100 = 2 (y – 100), y + 10 = 6 (x – 10)][/su_note]
[su_label]हल : मान लीजिए रेलगाड़ी की चाल = ???? km/h[/su_label]
और रेलगाड़ी द्वारा लिया गया समय = y घंटे
∴ गाड़ी द्वारा तय की गई दूरी
= (चाल) x (समय)
= (????y) km
पहली शर्त अनुसार,
(???? + 10) (y – 2) = ????y
या ????y – 2???? + 10y – 20 = ????y
या – 2???? + 10 – 20 = 0
या ???? – 5y + 10 = 0 …(1)
दूसरी शर्त अनुसार,
(???? – 10) (y + 3) = ????y
या ????y + 3???? – 10y – 30 = ????y
या 3???? – 10y – 30 = 0
(1) को 3 से गुणा करने पर हमें प्राप्त होता है :
3???? – 15y + 30 = 0
अब, (3) – (2) से प्राप्त होता है
3???? – 15y + 30 = 0
3???? – 10y – 30 = 0
– + +
– 5y + 60 = 0
या -5y = – 60
या 
y के इस मान को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है:
???? – 5 x 12 + 10 = 0
या ???? – 60 + 10 = 0
या ???? – 50 = 0 या
या ???? = 50
∴ रेलगाड़ी की चाल = 50 km/h
रेलगाड़ी द्वारा लिया गया समय
= 12 घंटे
अतः, रेलगाड़ी द्वारा तय की गई दूरी
= (50 x 12) km
= 600 km
[su_note]प्रश्न 4. एक कक्षा के विद्यार्थियों को पंक्तियों में खड़ा किया जाना है। यदि प्रत्येक पंक्ति में 3 विद्यार्थी अतिरिक्त हों, तो एक पंक्ति कम होगी। यदि एक पंक्ति में 3 विद्यार्थी कम हों, तो 2 पंक्तियाँ अधिक होंगी। कक्षा में विद्यार्थियों की संख्या ज्ञात कीजिए।[/su_note]
[su_label]हल : मान लीजिए प्रत्येक पक्ति में विद्यार्थियों की संख्या = x[/su_label]
और पंक्तियों की संख्या = y
कक्षा में विद्यार्थियों की संख्या = ????y
पहली शर्त अनुसार
(???? + 3) (y – 1) = ????y
या ????y – ???? + 3y – 3 = ????y
या – ???? + 3y – 3 = 0
या ???? – 3y + 3 =0
दूसरी शर्त अनुसार
(???? – 3) (1 + 2) = ????y
या y + 2???? – 3 – 6 = ????y
या 2???? – 3y – 6 = 0
अब, (2) – (1) से प्राप्त होता है :
2???? – 3y – 6 = 0
???? – 3y + 3 = 0
– + –
???? – 9 = 0
x = 9
???? को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है।
9 – 3y + 3 = 0
या – 3y + 12 = 0
या – 3y = – 12
या y = 12 = 4
या y 
∴ प्रत्येक पंक्ति में विद्यार्थियों की संख्या = 9
और पँक्तियों की संख्या = 4
अतः, कक्षा में विद्यार्थियों की संख्या = 9 x 4 = 36
[su_note]प्रश्न 5. एक ∆ABC में ∠C = 3 ∠B = 2 (∠A + ∠B) है। तीनों कोण ज्ञात कीजिए।[/su_note]
[su_label]हल : एक ∆ABC में,[/su_label]
∠C = 3∠B = 2 (∠A + ∠B)
I II III
II और III, से हमें प्राप्त होता है
3∠B = 2 (∠A + ∠B)
या 3∠B = 2∠A + 2∠B
या 3∠B – 2∠B = 2∠A
या ∠B = 2∠A …(1)
I और II, से हमें प्राप्त होता है
∠C = 3∠B
या LC = 3(2∠A) [(1) का प्रयोग करने पर]
या LC = 6∠A …(2)
त्रिभुज के तीनों कोणों का योगफल 180° होता है
∠A + ∠B + ∠C = 180°
या ∠A + 2∠A + 6∠A = 180°
9∠A = 180°
या 
∴ 9∠A = 20°; ∠B = 2 x 20° = 40°
∠C = 6 x 20° = 120°.
[su_note]प्रश्न 6. समीकरणों 5x – y = 5 और 3x – y = 3 के आलेख खींचिए। इन रेखाओं और y-अक्ष द्वारा बनी त्रिभुज के शीर्षों के निर्देशांक ज्ञात कीजिए।[/su_note]
[su_label]हल : दिया गया रैखिक समीकरण युग्म है :[/su_label]
5???? – y = 5 और 3???? – y = 3
5???? – y = 5
या 5???? = 5 + y
या 
…(1)
y = 0 को (1), रखने पर, हमें प्राप्त होता है :
y = – 5 को (1) में रखने पर, हमें प्राप्त होता है :
y = 5 को (1) में रखने पर, हमें प्राप्त होता है :
सारणी
| ???? | 1 | 0 | 2 |
| y | 0 | -5 | 5 |
| (x, y) | (1, 0) | (0, – 5) | (2, 5) |
बिंदुओं A (1, 0); B (0, – 5); C (2, 5) को ग्राफ पर आलेखित करने पर हमें समीकरण 5???? – y = 5 की रेखा प्राप्त होती है।
और 3???? – y = 3 या
या 3???? = 3 + y
या 
…(2)
y = 0 को (2) में रखने पर, हमें प्राप्त होता है :
y = – 3 को (2) में रखने पर, हमें प्राप्त होता है :
y = 3 को (2) में रखने पर, हमें प्राप्त होता है :
सारणी
| ???? | 1 | 0 | 2 |
| y | 0 | -3 | 3 |
| (x, y) | (1, 0) | (0, – 3) | (2, 3) |
बिंदुओं A (1, 0); D (0, – 3); E (2, 3) को ग्राफ पेपर आलेखित करने पर हमें समीकरण 3x – y = 3 की रेखा प्राप्त होती है :
ग्राफ से यह स्पष्ट है कि दी गई रेखाएँ A (1, 0) पर प्रतिच्छेद करती हैं। इन रेखाओं और -अक्ष से बनी AABD को छायांकित किया गया है। AABD के शीर्षों के निर्देशांक हैं : A (1, 0); B (0, – 5) और D (0, – 3)
[su_note]प्रश्न 7. निम्नलिखित रैखिक समीकरणों के युग्म की हल कीजिए[/su_note]
(i) px + qy = p – q
qx – py = p + q
(ii) ax + by = c
bx + ay = 1 + c
(iii) 
ax + ay = a2 + b
(iv) (α – b)???? + (α + b) y = α2 – 2αb – b2
(α + b) (???? + y) = α2 + b2
(v) 152???? – 378y = – 74
– 378???? + 152y = – 604
[su_label]हल : (i) दिया गया रैखिक समीकरण युग्म है :[/su_label]
p???? + qy = p – q …(1)
और q???? – py = p + q …(2)
(1) को q से और (2) को p से गुणा करने पर हमें प्राप्त होता है।
pq???? + q2y = pq – q2
pq???? – p2y = pq + p2
– + – –
(q2 + p2) y = – (q2 + p2)
या y = – 1
y के इस मान को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
p???? + q (-1) = p – q
या p???? – q = p – q
या p???? = p – q + q
या p???? = p
या ???? = 1
अतः, ???? = 1 और y = – 1
[su_label](ii) दिया गया रैखिक समीकरण युग्म है :[/su_label]
α???? + by = c
और b???? + αy = 1 + c
या α???? + by – c = 0
और b???? + αy – (1 + c) = 0
I और III से हमें प्राप्त होता है :
या 
II और III से हमें प्राप्त होता है :
या 
अतः 
और 
[su_label](iii) दिया गया रैखिक समीकरण युग्म है :[/su_label]
या 
या b???? – αy = 0
और α???? + by = α2 + b2 …(1)
या α???? + by – (α2 + b2) = 0 …(2)
या 
या 
I और III से हमें प्राप्त होता है :
II और III से हमें प्राप्त होता है :
अतः, ???? = α और y = b
[su_label](iv) दिया गया रैखिक समीकरण युग्म है :[/su_label]
(α – b)???? + (α + b)y = α2 – 2αb – b2
या α???? – b???? + αy + by = α2 – 2αb – b2
और (α + b) (???? + y) = α2 + b2
या α???? + b???? + αy + by = α2 + b2
अब, (1) – (2) से प्राप्त होता है:
α???? – b???? + αy + by = α2 – 2αb – b2
α???? + b???? + αy + by = α2 + b2
– – – –
– 2b???? = – 2αb – 2b2
– 2b???? = – 2b [α + b]
= ???? = α + b
???? के इस मान को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
(α – b) (α + b) + (α + b) y = α2 – 2αb – b2
या α2 – b2 + (α + b) y = α2 – 2αb – b2
या (α2 + b2) y = α2 – 2αb – b2 – α2 + b2
या (α + b) y = – 2αb
या 
अतः, ???? = α + b और
[su_label](v) दिया गया रैखिक समीकरण युग्म है :[/su_label]
152???? – 378y = – 74
और – 378???? + 152y = – 604
या 76???? – 189y + 37 = 0
और – 189???? + 76y + 302 = 0
या 
या 
I और III से हमें प्राप्त होता है
⇒ 
⇒ ???? = 2
II और III से हमें प्राप्त होता है
⇒ 
⇒ y = 1
अतः, ???? = 2 और y = 1
[su_note]प्रश्न 8. ABCD एक चक्रीय चतुर्भुज है। देखिए आकृति। चक्रीय चतुर्भुज के कोण ज्ञात कीजिए।[/su_note]
[su_label]हल : चक्रीय चतुर्भुज ABCD में,[/su_label]
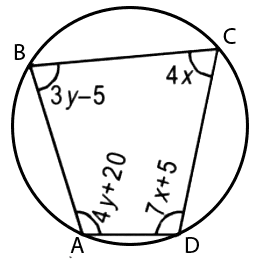
∠A = (4y + 20); ∠B = 3y – 5;
∠C = 4???? और ∠D = 7???? + 5
∠C = 4???? = 4 x 15 = 60°
∠D = 7???? + 5 = 7 x 15 + 5 = 110°
अतः, ∠A = 120°, ∠B = 70°; ∠C = 60°
और ∠D = 110°
∴ ∠A + ∠C = 180°
या 4y + 20 + (4????) = 180°
या 4???? + 4y = 180° – 20
या 4???? + 4y = 160
या ???? + y = 40
या y = 40 – ???? …(1)
और ∠B + ∠D = 180°
या 3y – 5 + (7???? + 5) = 180°
या 3 – 5 + 7???? + 5 = 180°
या 7???? + 3y = 180° …(2)
(1) से y के इस मान को (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
7???? + 3 (40 – ????) = 180°
7???? + 120 – 3???? = 180
या 4???? = 180 – 120
या 4???? = 60
या 
???? के इस मान को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है:
y = 40 – 15 = 25
∴ ∠A = 4y + 20 = 4 x 25 + 20 = 120°
∠B = 3y – 5 = 3 x 25 – 5 = 70°
∠C = 4???? = 4 x 15 = 60°
∠D = 7???? + 5 = 7 x 15 + 5 = 110°
अतः ∠A = 120°, ∠B = 70°; ∠C = 60°
और ∠D = 110°
इस पोस्ट में आपको Class 10 Maths Chapter 3 Exercise 3.7 Class 10 Chapter 3 Maths Pair of Linear Equations in Two Variables Exercise 3.7 class 10 maths chapter 3 notes class 10 maths chapter 3 exercise 3.7 solutions Class 10 अध्याय 3 दो चरों वाले रैखिक समीकरणों का युग्म प्रश्नावली 3.7 कक्षा 10 गणित अध्याय 3 प्रश्नावली 3.7 दो चर वाले रैखिक समीकरण युग्म क्लास 10th से संबंधित पूरी जानकारी दी गई है अगर इसके बारे में आपका कोई भी सवाल या सुझाव हो तो नीचे कमेंट करके हम से जरूर पूछें और अगर आपको यह जानकारी फायदेमंद लगे तो अपने दोस्तों के साथ शेयर जरूर करें.
Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.1
Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.2
Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.3
Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.4
Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.5
Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.6
Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.7