Class 10 Maths Chapter 3 Exercise 3.5 – दो चर वाले रैखिक समीकरण युग्म
जो विद्यार्थी 10वीं कक्षा में पढ़ रहे है उनके लिए यहां पर एनसीईआरटी कक्षा 10 गणित अध्याय 3. (दो चर वाले रैखिक समीकरण युग्म) प्रश्नावली 3.5 के लिए सलूशन दिया गया है. जोकि एक सरल भाषा में दिया है .ताकि विद्यार्थी को पढने में कोई दिक्कत न आए .इसकी मदद से आप अपनी परीक्षा में अछे अंक प्राप्त कर सकते है. इसलिए निचे आपको एनसीईआरटी समाधान कक्षा 10 गणित अध्याय 3 दो चर वाले रैखिक समीकरण युग्म प्रश्नावली 3.5 दिया गया है .
Class 10th Maths दो चर वाले रैखिक समीकरण युग्म (प्रश्नावली 3.5)
(i) x – 3y – 3 = 0
3x – 9y – 2 = 0
(ii) 2x + y = 5
3x + 2y = 8
(iii) 3x – 5y = 20
6x – 10y = 40
(iv) x – 3y – 7 = 0
3x – 3y – 15 = 0
???? – 3y – 3 = 0
और 3???? – 9y – 2 = 0
यहाँ α1 = 1, b1 = – 3, c1 = – 3
α2 = 3, b2 = – 9, c2, = – 2
अब ![]()
![]()
∴ ![]()
अतः दी गई समीकरण निकाय का कोई हल नहीं है।
(ii) दिया गया रैखिक समीकरण युग्म है :2???? + y = 5
और 3???? + 2y = 8
या 2???? + y – 5 = 0
और 3???? + 2y – 8 = 0
यहाँ α1 = 2, b1 = 1, c1 = – 5
α2 = 3, b2 = 2, c2 = – 8
अब ![]()
∴ ![]()
∴ दिए गए समीकरण निकाय का एक अद्वितीय हल है।
![]()
या ![]()
या ![]()
I II III
I और III से हमें प्राप्त होता है :
![]()
II और III से हमें प्राप्त होता है :
![]()
अतः, ???? = 2 और y = 1
(iii) दिया गया रैखिक समीकरण युग्म है :3???? – 5y = 20
और 6???? – 10y = 40
या 3???? – 5y – 20 = 0
और 6???? – 10y – 40 = 0
यहाँ α1 = 3, b1 = – 5, c1 = – 20
α2 = 6, b2 = – 10, c2 = – 40
![]()
![]()
![]()
∵ ![]()
अतः, दी गई समीकरण निकाय के अपरिमित रूप से अनेक हल हैं।
(iv) दिया गया रैखिक समीकरण युग्म है :???? – 3y – 7 = 0
और 3???? – 3y – 15 = 0
यहाँ α1 = 1, b1 = – 3, c1 = – 7
α2 = 3, b2 = – 3, c2 = – 15
अब ![]()
![]()
∴ ![]()
दिए गए समीकरण निकाय का एक अद्वितीय हल है
![]()
या ![]()
![]()
या ![]()
I और III से, हमें प्राप्त होता है
![]()
II और III से हमें प्राप्त होता है
![]()
यहाँ, ???? = 4, y = – 1
2???? + 3y = 7
और (a – b) x + (a + b) y = 3a + b – 2
(ii) k के किस मान के लिए निम्नलिखित समीकरण निकाय का कोई हल न होगा।
3???? + y = 1
(2k – 1) x + (k – 1) y = 2k + 1
2???? + 3y = 7
और (α – b) x + (α + b) y = 3α + b – 2
या 2???? + 3y – 7 = 0
और (α – b) ???? + (α + b) y – (3α + b – 2) = 0
यहाँ α1 = 2, b1 = 3, c1 = – 7
α2 = α – b, b2 = α + b,
c2 = – (3α + b – 2)
∴ दी गई समीकरण निकाय के अपरिमित रूप से अनेक हल हैं:
∴ ![]()
![]()
I और III से, हमें प्राप्त होता है :
![]()
या 6α + 2b – 4 = 7α – 7b
या – α + 9b – 4 = 0
या α = 9b – 4 …..(1)
II और III से प्राप्त होता है :
![]()
या 9α + 3b – 6 = 7α + 7b
या 2α – 4b – 6 = 0
या α – 2b – 3 = 0
समीकरण (1) से α का मान उपरोक्त में प्रतिस्थापित करने पर :
9b – 4 – 2b – 3 = 0
या 7b – 7 = 0
या 7b = 7
या b = 1
b के इस मान को (1) में प्रतिस्थापित करने पर हम प्राप्त करते हैं :
α = 9 x 1 – 4
= 9 – 4
α = 5
अतः α = 5 और b = 1
(ii) दिया गया रैखिक समीकरण युग्म है :3???? + y = 1
और 2k – 1) ???? + (k -1 1) y = 2k + 1
या 3???? + y – 1 = 0
और (2k – 1) x + (k – 1) y – (2k + 1) = 0
यहाँ α1 = 3, b1 = 1, c1 = – 1
α2 = (2k – 1), b2 = k – 1,
c2 = – (2k + 1)
∴ दी गई समीकरण निकाय का कोई हल नहीं है
∴ ![]()
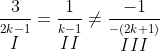
I और III से हमें प्राप्त होता है :
![]()
⇒ 4k ≠ – 4
⇒ ![]()
⇒ k ≠ – 1
I और II से हमें प्राप्त होता है :
![]()
⇒ k = 2
अतः, k = 2 और k ≠ – 1
प्र
8x + 5y = 9
3x + 2y = 4
8x + 5y = 9 ….(1)
3x + 2y = 4 ….(2)
प्रतिस्थापन विधि
(2) से, 2y = 4 – 3????
![]() ….(3)
….(3)
y के इस मान का (1), में प्रतिस्थापित करने पर हमें प्राप्त होता है :
![]()
या ![]()
या ???? = 18 – 20 = – 2
???? का यह मूल्य (3) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
![]()
![]()
अतः, ???? = – 2 और y = 5
वज्र गुणनविधि द्वारा
रैखिक समीकरण युग्म
8???? + 5y – 9 = 0
और 3???? + 2y – 4 = 0
यहाँ α1 = 8, b1 = 5, c1 = – 9
α2 = 3, b2 = 2, c2 = – 4
अब, ![]()
∵ ![]()
∴ निकाय का एक अद्वितीय हल है।
![]()
या ![]()
I और III से हमें प्राप्त होता है :
![]()
II और III से हमें प्राप्त होता है :
![]()
अंत:, ???? = – 2 और y = 5
(ii) एक भिन्न
(iii) यश ने एक टेस्ट में 40 अंक अर्जित किए, जब उसे प्रत्येक सही उत्तर पर 3 अंक मिले तथा अशुद्ध उत्तर पर 1 अंक की कटौती की गई। यदि उसे सही उत्तर पर 4 अंक मिलते हैं तथा अशुद्ध उत्तर पर 2 अंक कटते, तो यश 50 अंक अर्जित करता। टेस्ट में कितने प्रश्न थे ? दो चरों वाले रैखिक समीकरण
(iv) एक राजमार्ग पर दो स्थान A और B 100 km की दूरी पर
हैं। एक कार A से तथा दूसरी कार B से एक ही समय चलना प्रारम्भ करती है। यदि ये कारें भिन्न-भिन्न चालों से एक ही दिशा में चलती है, तो वे 5 घंटे पश्चात मिलती है। दोनों कारों की चाल ज्ञात कीजिए।
(v) एक आयत का क्षेत्रफल 9 वर्ग इकाई कम हो जाता है, यदि उसकी लंबाई 5 इकाई कम कर दी जाती है और चौड़ाई 3 इकाई बढ़ा दी जाती है। यदि हम लंबाई को 3 इकाई और चौड़ाई बढ़ा दें, तो क्षेत्रफल 67 वर्ग इकाई बढ़ जाता है। आयत की विमाएँ ज्ञात कीजिए।हल : (i) मान लीजिए होस्टल का नियत मासिक किराया = ₹ ????
और प्रतिदिन भोजन का मूल्य = ₹ y
पहली शर्त के अनुसार,
???? + 20y = 1000 ….(1)
प्रश्न की दूसरी शर्त अनुसार,I
???? + 26y = 1180 ….(2)
![]()
या ![]()
या ![]()
I और III से हमें प्राप्त होता है :
![]()
II और III से हमें प्राप्त होता है :
![]()
अतः होस्टल का मासिक नियत किराया और प्रतिदिन भोजन का मूल्य क्रमश: ₹ 400 और ₹ 30 है।
(ii) मान लीजिए भिन्न का अंश = ????निम्न का हर = y
∴ अभीष्ट भिन्न = ![]()
पहली शर्त के अनुसार,
![]()
या 3????-3=y
या 3???? -y – 3 = 0 ….(1)
दूसरी शर्त अनुसार,
![]()
या 4???? = y + 8
या 4???? – y – 8 = 0 ….(2)
![]()
I और III से हमें प्राप्त होता है :
![]()
II और III से हमें प्राप्त होता है :
![]()
अतः, अभीष्ट भिन्न ![]()
और यश द्वारा किए गए गलत प्रश्नों की संख्या = y
पहली शर्त अनुसार,
3???? – y = 40
या 3???? – y – 40 = 0 ….(1)
दूसरी शर्त अनुसार,
4???? – 2y = 50
या 4???? – 2y – 50 = 0 ….(2)
![]()
या ![]()
I और III से हमें प्राप्त होता है :
![]()
⇒ ![]()
⇒ ???? = 15
II और III से हमें प्राप्त होता है :
![]()
⇒ ![]()
⇒ y = 5
∴ सही प्रश्नों की संख्या = 15
गलत प्रश्नों की संख्या = 5
अतः प्रश्नों की कुल संख्या
= [सही प्रश्नों की संज्या] + [ गलत प्रश्नों की संज्या]
= 15 + 5 = 20
(iv) मान लीजिए स्थान A वाली कार की चाल= ???? km/h
और स्थान B वाली कार की चाल = y km/h
A और B के बीच की दूरी = 100 km
5 घंटे की स्थिति में
कार A द्वारा तय की गई दूरी = 5???? km [∵ दूरी = चाल x समय]
कार B द्वारा तय की गई दूरी = 5y km
पहली शर्त अनुसार,
5???? – 5y = 100
या ???? – y = 20
या ???? – y – 20 = 0 ….(1)
एक घंटे की स्थिति में
कार A द्वारा तय की गई दूरी = ???? km [∵ दूरी = चाल x समय]
कार B द्वारा तय की गई दूरी = y km
दूसरी शर्त अनुसार,
???? + y = 100
या ???? + y – 100 = 00 …(2)
![]()
![]()
या ![]()
II और III से हमें प्राप्त होता है :
![]()
I और III से हमें प्राप्त होता है :
![]()
अतः, बिंदुओं A तथा B से चलने वाली कारों की चालें क्रमश: 60 km/h और 40 km/h है।
(v) मान लीजिए आयत की लंबाई = ???? मात्रकऔर आयत की चौड़ाई = y मात्रक
∴ आयत का क्षेत्रफल = ????y sq. मात्रक
पहली शर्त अनुसार,
(???? – 5) (y + 3) = ????y – 9
या ????y + 3???? – 5y – 15 = ????y – 9
या 3???? – 5y – 6 = 0 ….(1)
दूसरी शर्त अनुसार,
(???? + 3) (y + 2) = ????y + 67
या ????y + 2???? + 3y + 6 = ????y + 67
या 2???? + 3y – 61 = 0 ….(2)
![]()
या ![]()
या ![]()
I और III से हमें प्राप्त होता है :
![]()
II और III से हमें प्राप्त होता है
![]()
अत: आयत की लंबाई और चौड़ाई क्रमशः 17 मात्रक और 9 मात्रक है।
इस पोस्ट में आपको Class 10 Maths Chapter 3 Exercise 3.5 class 10 maths chapter 3 solutions class 10 maths chapter 3 solutions pdf download class 10 maths chapter 3 exercise 3.5 solutions class 10 maths chapter 3 notes class 10 maths chapter 3 exercise 3.3 solutions NCERT Class-10 प्रश्नावली 3.5 Mathematics 3. दो चर वाले रैखिक समीकरण युग्म कक्षा 10 गणित अध्याय 3 प्रश्नावली 3.5 कक्षा 10 गणित प्रश्नावली 3.5 समाधान से संबंधित पूरी जानकारी दी गई है अगर इसके बारे में आपका कोई भी सवाल या सुझाव हो तो नीचे कमेंट करके हम से जरूर पूछें और अगर आपको यह जानकारी फायदेमंद लगे तो अपने दोस्तों के साथ शेयर जरूर करें.
Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.1
Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.2
Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.3
Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.4
Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.5
Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.6
Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.7