Class 10 Maths Chapter 3 Exercise 3.4 – दो चर वाले रैखिक समीकरण युग्म

Class 10 Maths Chapter 3 Exercise 3.4 – दो चर वाले रैखिक समीकरण युग्म

कक्षा 10वीं के विद्यार्थी के लिए यहां पर एनसीईआरटी कक्षा 10 गणित अध्याय 3. (दो चर वाले रैखिक समीकरण युग्म ) प्रश्नावली 3.3 के लिए सलूशन दिया गया है. जोकि एक सरल भाषा में दिया है .ताकि विद्यार्थी को पढने में कोई दिक्कत न आए .इसकी मदद से आप अपनी परीक्षा में अछे अंक प्राप्त कर सकते है.

Class 10th Maths दो चर वाले रैखिक समीकरण युग्म (प्रश्नावली 3.4)

(i) ???? + y = 5 और 2x – 3y = 4

(ii) 3???? + 4y = 10 और 2x – 2y = 2

(iii) 3x – 5y – 4 = 0 और 9x = 2y + 7

(iv) और

हल : (i) दिये गये रैखिक समीकरणों का युग्म है :

???? + y = 5 …..(1)

और 2???? – 3y = 4 …..(2)

विलोपन विधि (1) को 2, से गुणा करने पर हम प्राप्त करते हैं।

2???? + 2y = 10 …..(3)

अब, (3) – (2) से प्राप्त होता है

2???? + 2y = 10

2???? – 3y = 4

या

y का यह मान (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है

या

अतः और

प्रतिस्थापन विधि

(2) से, 2???? = 4 + 3y

या …(4)

???? का यह मान (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है

या

या 4 + 5y = 10

या 5y = 10 – 4 = 6

या

y का यह मान (4) में प्रतिस्थापित करने पर हमें प्राप्त होता है

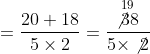
अत: और

(ii) दिया गया रैखिक समीकरण युग्म है :

3???? + 4y = 10

और 2x – 2 = 2

विलोपन विधि समीकरण (2) को 2 से गुणा करने पर हमें प्राप्त होता है :

4???? – 4y = 4

अब, (3) + (1) देता है :

4???? – 4y = 4

3???? + 4y = 10

7???? = 14

या

???? का यह मान (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है

3 (2) + 4y = 10

या 6 + 4y = 10

या 4y = 10 – 6

या 4y = 4

या

अतः, ???? = 2 और y = 1

प्रतिस्थापन विधि

(2) से,

2???? = 2 + 2y

???? = y + 1

???? का यह मान (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है

3 (y + 1) + 4y = 10

या 3y + 3 + 4y = 10

या 7y = 10 – 3

या 7y = 7

या y = 1

y का यह मान (3) में प्रतिस्थापित करने पर हमें प्राप्त होता है

???? = 1 + 1 = 2

अतः, ???? = 2 और y = 1

(iii) दिया गया रैखिक समीकरण युग्म हैं :

3???? – 5y – 4 = 0 …..(1)

और 9???? = 2y + 7

या 9???? – 2y – 7 = 0 …..(2)

विलोपन विधि

(1) को 3 से गुणा करने पर हमें प्राप्त होता है

9???? – 15y – 12 = 0

अब, (3) – (2) से प्राप्त होता है

9???? – 15y – 12 = 0

9???? – 2y – 7 = 0

– + +

– 13y – 5 = 0

– 13y = 5

y का यह मान (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है

या

या

या

या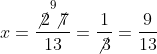

अत और

प्रतिस्थापन विधि

(2) से, …(4)

???? का यह मान (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है

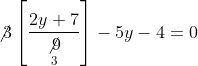
या

या – 13y – 5 = 0

या – 13y = 5

या

y का यह मान (4) में प्रतिस्थापित करने पर हमें प्राप्त होता है

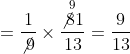
अतः, और

(iv) दिया गया रैखिक समीकरण युग्म है :

या

या 3???? + 4y = – 6 …..(1)

या

या 3???? – y = 9 …..(2)

विलोपन विधि

(1) – (2) से प्राप्त होता है

3???? + 4y = – 6

3???? – y = 9

– + –

5y = – 15

या

y का यह मान (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :

3???? + 4 (- 3) = – 6

या 3???? – 12 = – 6

3???? = – 6 + 12

या 3???? = 6

या

अतः ???? = 2, y = – 3

प्रतिस्थापन विधि

(2) से, y = 3???? – 9 ….(4)

y का यह मान (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :

3???? + 4 (3???? – 9) = – 6

या 3???? + 12???? – 36 = – 6

या 15???? = – 6 + 36

या 15???? = 30

या

???? का यह मान (4) में प्रतिस्थापित करने पर हमें प्राप्त होता है :

y = 3 (2) – 9

= 6 – 9 = – 3

अतः, ???? = 2, y = – 3

(i) यदि हम अंश में 1 जोड़ दें तथा हर में से 1 घटा दें, तो भिन्न 1 में बदल जाती है। यदि हर में 1 जोड़ दें, तो यह बन जाती है। वह भिन्न क्या है?
(ii) पाँच वर्ष पूर्व, नूरी की आयु, सोनू की आयु की तीन गुनी थी दस वर्ष पश्चात् नूरी की आयु, सोनू की आयु की दो गुनी हो जाएगी। नूरी और सोनू की आयु कितनी है ?
(iii) दो अंकों की एक संख्या का योग 9 है। इस संख्या के अंकों को पलटने से बनी संख्या का दो गुना है। इस वह संख्या ज्ञात कीजिए।
(iv) मीना ₹ 2000 निकालने के लिए बैंक गई। उसने खजांची से ₹ 50 तथा ₹ 100 के नोट देने के लिए कहा। मीना ने कुल 25 नोट प्राप्त हुए। ज्ञात कीजिए उसे ₹ 50 और ₹ 100 के कितने-कितने नोट प्राप्त हुए।
(v) किराये पर पुस्तकें देने वाले किसी पुस्तकालय का प्रथम दिनों का एक नियत किराया है तथा उसके बाद प्रत्येक अतिरिक्त दिन का अलग किराया है। सरिता ने सात दिनों तक एक पुस्तक रखने के लिए ₹ 27 अदा किए, जबकि सूसी ने एक पुस्तक पाँच दिनों तक रखने के ₹ 21 अदा किए। नियत किराया तथा प्रत्येक अतिरिक्त दिन का किराया ज्ञात कीजिए।हल : (i) मान लीजिए भिन्न का अंश = ????

भिन्न का हर = y

∴ अभीष्ट भिन्न

पहली शर्त के अनुसार,

या ???? + 1 = y – 1

या ???? – y + 2 = 0

दूसरी शर्त के अनुसार,

या 2???? = y + 1

या 2???? – y – 1 = 0 ……(2)

अब, (2) – (1) से प्राप्त होता है

2???? – y – 1 = 0
???? – y + 2 = 0
– + –
———-
???? – 3 = 0

या ???? = 3

???? का यह मान (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है :

2 x 3 – y – 1 = 0

या 6 – y – 1 = 0

या 5 – y = 0

या y = 5

अतः, अभीष्ट भिन्न में है।
(ii) मान लीजिए नूरी की वर्तमान आयु = ???? वर्ष

• सोनू की वर्तमान आयु = y वर्ष
• पाँच वर्ष पहले
• नूरी की आयु = (???? – 5) वर्ष
• सोनू की आयु = (y – 5) वर्ष
• पहली शर्त अनुसार,
• ???? – 5 = 3 (y – 5)
• या ???? – 5 = 3y – 15
• या ???? – 3y + 10 = 0 …(1)

दस वर्ष बाद

नूरी की आयु = (???? + 10) वर्ष

सोनू की आयु = (y + 10) वर्ष

दूसरी शर्त के अनुसार,

???? + 10 = 2 (y + 10)

या ???? + 10 = 2y + 20

या ???? – 27 – 10 = 0 ……(2)

अब, (1) – (2) से प्राप्त होता है

???? – 3y + 10 = 0

???? – 2y – 10 = 0
– + +
—————-
– y + 20 = 0

या – y = – 20

या y = 20

y का यह मान (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है :

???? – 2(20) – 0 = 0

या ???? – 40 – 10 = 0

या ???? = 50

अतः, नूरी की वर्तमान आयु = 50 वर्ष

सोनू की वर्तमान आयु = 20 वर्ष

(iii) मान लीजिए इकाई का अंक = ????

दहाई का अंक = y

∴ अभीष्ट संख्या = 10y + ????

पहली शर्त के अनुसार,

???? + y = 9

उल्टाने पर

इकाई का अंक = y

दहाई का अंक = ????

संख्या = 10???? + y

दूसरी शर्त अनुसार,

या 9 [10y + ????] = 2[10???? + y]

या 90y + 9???? = 20???? + 2y

या 90y + 9???? – 20???? – 2y = 0

– 11???? + 88y = 0

???? – 8y = 0

अब, (2) – (1) से प्राप्त होता है

???? – 8y = 0

???? + y = 9
– – –
————–
– 9y = – 9

y = 1

y का यह मान (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है :

???? – 8 x 1 = 0

या ???? = 8

अतः, अभीष्ट संख्या = 10y + x

= 10 x 1 + 8 = 18

(iv) मान लीजिए मीना को मिले ₹ 50 के नोटों की संख्या = ????

साथ ही, मीना को प्राप्त ₹ 100 के नोटों की संख्या = y

पहली शर्त के अनुसार, ……(1)

???? + y = 25

दूसरी शर्त के अनुसार,

50???? + 100y = 2000

या ???? + 2y = 40 ……(2)

अब, (2) – (1) से प्राप्त होता है

???? + 2y = 40

???? + y = 25
– – –
————-

y = 15

y का यह मान (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :

???? + 15 = 25

या ???? = 25 – 15 = 10

अतः, मीना को मिले ₹ 50 और ₹ 100 के नोटों की संख्या क्रमश: 10 और 15 है।

(v) मान लीजिए पहले तीन दिन के लिए निश्चित किराया = ₹ ????

उसके बाद प्रत्येक दिन के लिए अतिरिक्त किराया = ₹ y

सरिता की स्थिति में

???? + 4y = 27 …..(1)

सूसी की स्थिति में,

???? + 2y = 21 …..(2)

अब, (1) – (2) से प्राप्त होता है

???? + 4y = 27

???? + 2y = 21
– – –
—————

2y = 6

या

y का यह मान (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है :

???? + 2(3) = 21

या ???? + 6 = 21

या ???? = 21 – 6 = 15

अतः, पहले तीन दिन के लिए नियत किराया और उसके बाद प्रत्येक दिन के लिए अतिरिक्त किराया ₹ 15 और ₹ 3 है।

इस पोस्ट में आपको Class 10 Maths Chapter 3 Exercise 3.4 NCERT Solutions Class 10 Maths Chapter 3 Exercise 3.4 Pair of Linear Equations in Two Variables Ncert solutions class 10 maths chapter 3 pdf download class 10 maths chapter 3 exercise 3.4 solutions class 10 maths chapter 3 exercise 3.2 solutions pair of linear equations in two variables class 10 solutions कक्षा 10 गणित अध्याय 3 प्रश्नावली 3.4 कक्षा 10 गणित प्रश्नावली 3.4 दो चरों वाले रैखिक समीकरणों का युग्म से संबंधित पूरी जानकारी दी गई है अगर इसके बारे में आपका कोई भी सवाल या सुझाव हो तो नीचे कमेंट करके हम से जरूर पूछें और अगर आपको यह जानकारी फायदेमंद लगे तो अपने दोस्तों के साथ शेयर जरूर करें.

Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.1
Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.2
Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.3
Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.4
Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.5
Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.6
Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.7