Class 10 Maths Chapter 15 Exercise 15.2 – प्रायिकता
NCERT Solutions for Class 10 Maths Chapter 15 Probability Ex 15.2 – आज हम आप के लिए Class 10 Maths Chapter 15 लेकर आयें है। जो कि Class 10 Maths Exams के लिए अत्यन्त उपयोगी साबित होगी. कक्षा 10वीं के विद्यार्थी के लिए यहां पर एनसीईआरटी कक्षा 10 गणित अध्याय 15. (प्रायिकता) प्रश्नावली 15.2 के लिए सलूशन दिया गया है. जोकि एक सरल भाषा में दिया है .ताकि विद्यार्थी को पढने में कोई दिक्कत न आए .इसकी मदद से आप अपनी परीक्षा में अछे अंक प्राप्त कर सकते है.
NCERT Solutions For Class 10th Maths प्रायिकता (प्रश्नावली 15.2)
जब श्याम और एकता एक दुकान पर एक ही सप्ताह में जा रहे हैं। संभाव्य परिणाम है :
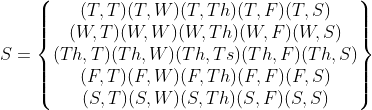
यहाँ T मंगलवार के लिए
W बुधवार के लिए
Th वीरवार के लिए
F शुक्रवार के लिए और
S शनिवार के लिए है।
n (S) = 25
(i) मान लीजिए ‘श्याम और एकता दुकान पर एक ही दिन जा रहे हैं’ घटना A है।
![]()
n(A) = 5
प्रायिकता कि दोनों एक ही दिन जाएंगे ![]()
(ii) मान लीजिए श्याम और एकता क्रमागत दिनों में जाएंगे घटना B है।
![]()
n(B) = 8
प्रायिकता कि दोनों क्रमागत दिनों में जाएंगे ![]()
(iii) प्रायिकता कि वह भिन्न दिनों में जाएंगे ![]()
(i) एक सम संख्या होगा ? (ii) 6 है ? (iii) कम से कम 6 है ?
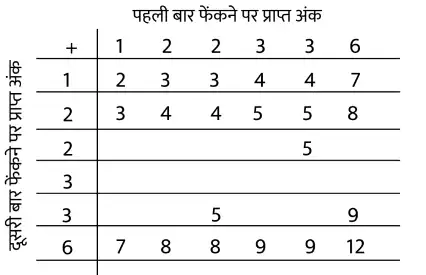
हल :पूर्ण सारणी है : पहली बार फेंकने पर प्राप्त अंक
| + | 1 | 2 | 2 | 3 | 3 | 6 |
| 1 | 2 | 3 | 3 | 4 | 4 | 7 |
| 2 | 3 | 4 | 4 | 5 | 5 | 8 |
| 2 | 2+1=3 | 2+2=4 | 2+2=4 | 2+3=5 | 2+3=5 | 2+6=8 |
| 3 | 3+1=4 | 3+2=5 | 3+2=5 | 3+3=6 | 3+3=6 | 3+6=9 |
| 3 | 3+1=4 | 3+2=5 | 3+2=5 | 3+3=6 | 3+3=6 | 9 |
| 6 | 7 | 8 | 8 | 9 | 9 | 12 |
संभाव्य परिणामों की संख्या है
6 x 6 = 36
(i) मान लीजिए ‘कुल योग एक सम संख्या’ प्राप्त करना घटना A है।
A = {2, 4, 4, 4, 4, 4, 4, 4, 4, 6, 6, 6, 6,8, 8, 8, 8, 12}
n (A) = 18
∴ एक सम संख्या प्राप्त करने की प्रायिकता
![]()
P (सम संख्या ) = ![]()
(ii) मान लीजिए ‘योग 6 प्राप्त करना’ घटना B है।
B = {6, 6, 6, 6}
n (B) = 4
कुल योग 6 प्राप्त करने की प्रायिकता ![]()
∴ ![]()
(iii) मान लीजिए ‘कुल योग कम से कम 6’ प्राप्त करना घटना C है।
C = {6, 6, 6, 6, 7, 7, 8, 8, 8, 8, 9, 9, 9, 9, 12}
n (C) = 15
∴ योग कम से कम 6 प्राप्त करने की प्रायिकता
![]()
∴ ![]()
हल : लाल गेंदों की संख्या = 5
मान लीजिए नीली गेंदों की संख्या = x
∴ गेंदों की कुल संख्या = 5 + x
नीली गेंदें निकालने की प्रायिकता ![]()
लाल गेंदें निकालने की प्रायिकता ![]()
प्रश्न के अनुसार,
नीली गेंद निकालने की प्रायिकता = 2 लाल गेंद निकालने की प्रायिकता
![]()
∴ नीली गेंदों की संख्या = 10
थैले में गेंदों की कुल संख्या = 12
काली गेंदों की संख्या = x
∴ काली गेंद प्राप्त करने की प्रायिकता ![]()
यदि थैले में 6 काली गेंदें और डाल दी जाएँ, तो पेटी में गेंदों की कुल संख्या = 12 + 6 = 18
काली गेंदों की संख्या = x + 6
काली गेंद प्राप्त करने की प्रायिकता ![]()
प्रश्न के अनुसार,
काली गेंद निकालने की प्रायिकता = 2 पहली स्थिति में काली गेंद निकालने की प्रायिकता
![]()
![]()
![]()
x + 6 = 3x
6 = 3x – x
6 = 2x
x = 3
∴ काली गेंदों की संख्या = 3
जार में कंचों की कुल की संख्या = 24
मान लीजिए हरे कंचों की संख्या = x
∴ नीले कंचों की संख्या = 24 – x
जब एक कंचा निकाला जाता है
हरा कंचा निकालने की प्रायिकता ![]()
![]()
![]()
x = 16
∴ हरे कंचों की संख्या = 16
∴ नीले कंचों की संख्या = 24 – x
= 24 – 16 = 8.
इस पोस्ट में आपको NCERT Solutions for Class 10 Maths chapter-15 Probability Exercise 15.2 Class 10 Math Exercise 15.2 Prayikta Class 10 maths chapter 15 exercise 15.2 probability class 10 maths chapter 15 exercise 15.2 solutions Class 10 maths chapter 15 questions Class 10 maths chapter 15 pdf Class 10 maths chapter 15 notes कक्षा 10 गणित अध्याय 15 प्रायिकता प्रश्नावली 15.2 कक्षा 10 गणित प्रायिकता प्रश्नावली 15.2 एनसीईआरटी कक्षा-10 प्रश्नावली 15.2 गणित 15. प्रायिकता से संबंधित पूरी जानकारी दी गई है अगर इसके बारे में आपका कोई भी सवाल या सुझाव हो तो नीचे कमेंट करके हम से जरूर पूछें और अगर आपको यह जानकारी फायदेमंद लगे तो अपने दोस्तों के साथ शेयर जरूर करें.
NCERT Solutions for Class 10 Maths Chapter 15 प्रायिकता Exercise 15.1
NCERT Solutions for Class 10 Maths Chapter 15 प्रायिकता Exercise 15.2