Class 10 Maths Chapter 15 Exercise 15.1 – प्रायिकता

Class 10 Maths Chapter 15 Exercise 15.1 – प्रायिकता

NCERT Solutions for Class 10 Maths Chapter 15 Probability Ex 15.1 – जो विद्यार्थी 10वीं कक्षा में पढ़ रहे है उनके लिए यहां पर एनसीईआरटी कक्षा 10 गणित अध्याय 15. (प्रायिकता) प्रश्नावली 15.1 के लिए सलूशन दिया गया है. जोकि एक सरल भाषा में दिया है .ताकि विद्यार्थी को पढने में कोई दिक्कत न आए .इसकी मदद से आप अपनी परीक्षा में अछे अंक प्राप्त कर सकते है. इसलिए निचे आपको एनसीईआरटी समाधान कक्षा 10 गणित अध्याय 15 प्रायिकता प्रश्नावली 15.1 दिया गया है .

NCERT Solutions For Class 10th Maths प्रायिकता (प्रश्नावली 15.1)

निम्न में से प्रत्येक के लिए रचना का औचित्य भी दीजिए :

(i) घटना E की प्रायिकता + घटना ‘E नहीं’ की प्रायिकता = ………. है।
(ii) उस घटना की प्रायिकता जो घटित नहीं हो सकती ………. है। ऐसी घटना …….. कहलाती है।
(iii) उस घटना की प्रायिकता जिसका घटित होना निश्चित है, ऐसी घटना ……….. कहलाती है।
(iv) किसी प्रयोग की सभी प्रारंभिक घटनाओं की प्रायिकताओं का योग …….. है।
(v) किसी घटना की प्रायिकता ……… से बड़ी या उसके बराबर होती है तथा ………. से छोटी या उसके बराबर होती है।
हल : (i) घटना E की प्रायिकता + घटना ‘E’ नहीं की प्रायिकता = 1 है।
(ii) उस घटना की प्रायिकता जो घटित नहीं हो सकती 0 है। ऐसी घटना असंभव घटना कहलाती है।
(iii) उस घटना की प्रायिकता जिसका घटित होना निश्चित है, ऐसी घटना निश्चित घटना कहलाती है।
(iv) किसी प्रयोग की सभी प्रारंभिक घटनाओं की प्रायिकताओं का योग 1 है।
(v) किसी घटना की प्रायिकता 0 से बड़ी या उसके बराबर होती है तथा 1 से छोटी या उसके बराबर होती है।

(i) एक ड्राइवर कार चलाने का प्रयत्न करता है। कार चलनी प्रारंभ हो जाती है या कार चलना प्रारंभ नहीं होती है।
(ii) एक खिलाड़ी बास्केटबॉल को बास्केट में डालने का प्रयत्न करती है। वह बास्केट में बॉल डाल पाती है या नहीं डाल पाती है।
(iii) एक सत्य-असत्य प्रश्न का अनुमान लगाया जाता है। उत्तर सही है या गलत होगा।
(iv) एक बच्चे का जन्म होता है। वह एक लड़का है या एक लड़की है।
हल :(i) जब एक ड्राइवर कार चलाने का प्रयत्न करता है, तो सामान्य स्थिति में कार चलने लगती है परंतु यदि कार में कोई दोष हो, तो कार नहीं चलती इसलिए परिणाम समप्रायिक नहीं है।
(ii) जब एक खिलाड़ी बास्केट बॉल को बास्केट में डालने का प्रयत्न करती है, तो इस स्थिति में परिणाम समप्रायिक नहीं हैं क्योंकि परिणाम कई तथ्यों पर निर्भर करता है जैसे खिलाड़ी का प्रशिक्षण, खिलाड़ी की ऊँचाई इत्यादि।
(iii) क्योंकि एक प्रश्न के लिए दो संभावनाएँ या तो सही या गलत हैं। सत्य असत्य के इस प्रश्न के इस अभिप्रयोग में एक ही परिणाम हो सकता है : सत्य या असत्य अर्थात् इस घटना के होने का एक ही अवसर है इसलिए दो परिणाम समप्रायिक हैं।
(iv) एक नव जन्मा बच्चा (जिसका जन्म इसी क्षण हुआ है) एक लड़का भी हो सकता है और एक लड़की भी हो सकती है और दोनों परिणाम समप्रायिक हैं।

जब सिक्के को उछाला जाता है तो केवल दो ही संभावनाएँ होती हैं अर्थात् परिणाम चित या पट दो समप्रायिक हैं। एक सिक्का उछालने के परिणाम की पूर्व भविष्यवाणी नहीं की जा सकती।

(A) (B) – 1.5 (C) 15% (D) 0.7.
हल :जैसा कि हम जानते हैं कि एक घटना की प्रायिकता 0 से कम और 1 से अधिक नहीं हो सकती अर्थात् 0 ≤ P (E) ≤ 1
∴ (B) – 1.5 संभव नहीं है।

दिया है (E) = 0.05
हम जानते हैं कि P(E) + P(E) नहीं = 1
= 0.05 + P(E) नहीं = 1
= P(E) नहीं = 1 – 0.05
= P(E) नहीं = 0.95

(i) संतरे कि महक वाली है ?
(ii) नींबू कि महक वाली है ?

माना थैले में कुल गोलियों की संख्या = n
(i) संतरे कि महक वाली है ?
संतरे की महक वाली गोलियों की संख्या = 0
संतरे की महक वाली गोली निकलने की प्रायिकता

नींबू कि महक वाली मीठी गोलियाँ संख्या = थैले में कुल गोलियों की संख्या = n
नींबू कि महक वाली गोली निकलने की प्रायिकता

P(E नहीं) = 0.9992

हम जानते है कि P(E) + P(E नहीं) = 1

अत: P(2 विधार्थियों के जन्मदिन एक ही दिन हो) + P(2 विधार्थियों के जन्मदिन एक ही न दिन हो) = 1
= P(2 विधार्थियों के जन्मदिन एक ही दिन हो) + 0.9992 = 1
= P(2 विधार्थियों के जन्मदिन एक ही दिन हो) = 1 – 0.9992
= P(2 विधार्थियों के जन्मदिन एक ही दिन हो) = 0.008 उत्तर

लाल गेंदों की संख्या = 3
काली गेंदों की संख्या = 5
गेदों की कुल संख्या = 3 + 5 = 8

एक गेंद यादृच्छया निकाली गई है

(i) लाल गेंद प्राप्त करने की प्रायिकता
P (लाल गेंद)

(ii) लाल गेंद न प्राप्त करने की प्रायिकता

= 1 – P (लाल गेंद)

लाल कंचों की संख्या = 5
सफेद कंचों की संख्या = 8
हरे कंचों की संख्या = 4
कंचों की कुल संख्या = 5 + 8 + 4 = 17
क्योंकि एक कंचा निकाला गया है

(i) लाल कंचे 5 हैं
लाल कंचा निकालने की प्रायिकता

(ii) क्योंकि सफेद कंचे 8 हैं।
सफेद कंचा निकालने की प्रायिकता

(iii) हरे कंचे 4 हैं।
हरा कंचा निकालने की प्रायिकता
∴ हरा कंचा न निकालने की प्रायिकता
= 1 – हरा कंचा निकालने की प्रायिकता

50 पैसे के सिक्कों की संख्या = 100
₹ 1 के सिक्कों की संख्या = 50
₹ 2 के सिक्कों की संख्या = 20
₹ 5 के सिक्कों की संख्या = 10
∴ सिक्कों की कुल संख्या = 100 + 50 + 20 + 10
= 180

(i) चूँकि 50 पैसे के 1200 सिक्के हैं
50 पैसे का सिक्का गिरने की प्रायिकता

p (50 p का सिक्का)

(ii) ₹ 5 के सिक्कों की संख्या = 10

∴ ₹ 5 का सिक्का गिरने की प्रायिकता

P (₹ 5 का सिक्का)

₹ 5 का सिक्का प्राप्त न करने की प्रायिकता

= 1 – P (₹ 5 का सिक्का)

नर मछलियों की संख्या = 5
मादा मछलियों की संख्या = 8
जल जीव कुण्ड में मछलियों की कुल संख्या = 5 + 8 = 13
नर मछली प्राप्त करने की प्रायिकता

P (नर मछली)

(i) 8 को?
(ii) एक विषम संख्या को?
(iii) 2 से बड़ी संख्या को?
(iv) 9 से छोटी संख्या को?

(i) परिणामों की कुल संख्या, {1, 2, 3, 4, 5, 6, 7, 8} = 8

‘8’ प्राप्त करने की प्रायिकता = 0

(ii) विषम संख्याएँ हैं = {1, 3, 5, 7}

विषम संख्या प्राप्त करने की प्रायिकता

(iii) 2 से बड़ी संख्याएँ हैं {3, 4, 5, 6, 7, 8}

∴ 2 से बड़ी संख्याएँ प्राप्त करने की प्रायिकता

P (2 से बड़ी संख्या)

(iv) 9 से छोटी संख्याएँ हैं :

{1, 2, 3, 4, 5, 6, 7, 8}

∴ 9 से छोटी संख्या प्राप्त करने की प्रायिकता

P (9 से छोटी संख्या) = 1

(i) एक अभाज्य संख्या
(ii) 2 और 6 के बीच स्थित कोई संख्या
(iii) एक विषम संख्या।

जब पासे को एक बार फेंका जाता है तो संभव परिणाम हैं
S = {1, 2, 3, 4, 5, 6}

(i) अभाज्य संख्याएँ हैं :

{2, 3, 5}

∴ अभाज्य संख्या प्राप्त करने की प्रायिकता

(ii) 2 और 6 के बीच स्थित संख्याएँ = {3, 4, 5}

2 और 6 के बीच स्थित संख्या प्राप्त करने की प्रायिकता

(iii) विषम संख्याएँ हैं = { 1, 3, 5}

एक विषम संख्या प्राप्त करने की प्रायिकता

P (एक विषम संख्या)

(i) लाल रंग का बादशाह
(ii) एक फेस कार्ड अर्थात् तस्वीर वाला पत्ता
(iii) लाल रंग की तस्वीर वाला पत्ता
(iv) पान का गुलाम
(v) हुकुम का पत्ता
(vi) एक ईंट की बेगम

52 पत्तों की एक गड्डी में पत्तों की संख्या 52 है।

(i) लाल रंग के दो बादशाह हैं

अर्थात् पान का बादशाह और ईंट का बादशाह लाल रंग का बादशाह प्राप्त करने की प्रायिकता

P (लाल रंग का बादशाह)

(ii) 12 फेस कार्ड हैं अर्थात् 4 गुलाम, 4 बेगम और 4 बादशाह

तस्वीर वाला पत्ता प्राप्त करने की प्रायिकता

∴ P (एक तस्वीर वाला पत्ता)

(iii) क्योंकि लाल रंग की तस्वीर के 6 पत्ते हैं अर्थात् 2 गुलाम 2 बेगम और 2 बादशाह हैं।

∴ 6 लाल रंग के फेस कार्ड प्राप्त करने की प्रायिकता

P (लाल रंग की तस्वीर वाला पत्ता)

(iv) पान का केवल एक ही गुलाम है।

∴ एक पान का गुलाम प्राप्त करने की प्रायिकता

P (पान का गुलाम)

(v) चूँकि हुकुम के 13 पत्ते हैं

∴ हुकुम का पत्ता प्राप्त करने की प्रायिकता

P (एक हुकुम का पत्ता)

(vi) चूँकि ईंट की बेगम केवल एक ही है

∴ ईंट की बेगम प्राप्त करने की प्रायिकता

P (ईंट की बेगम)

(i) इसकी क्या प्रायिकता है कि यह पत्ता एक बेगम है?
(ii) यदि बेगम निकल आती है, तो उसे अलग रख दिया जाता है और एक अन्य पत्ता निकाला जाता है। इसकी क्या प्रायिकता है कि दूसरा निकाला गया पत्ता (a) एक इक्का है ? (b) एक बेगम है ?

पाँच पत्ते ईंट का दहला, गुलाम, बेगम, बादशाह और इक्का हैं।

(i) बेगम प्राप्त करने की प्रायिकता
∴ P (एक बेगम)
(ii) यदि बेगम निकल आती है,

तो उसे अलग रख दिया जाता है तो चार पत्ते बच जाते हैं : ईंट का दहला, गुलाम, बादशाह और इक्का

(α) इक्का प्राप्त करने की प्रायिकता
P (एक इक्का)

कोई बेगम नहीं बची।

(b) बेगम प्राप्त करने की प्रायिकता
P (एक बेगम) = 0

खराब पेनों की संख्या = 12
अच्छे पेनों की संख्या = 132
∴ पेनों की कुल संख्या = 12 + 132 = 144

(i) दो अंकों वाली संख्या प्राप्त करने की प्रायिकता

∴ P (दो अंकों की एक संख्या)

(ii) पूर्ण वर्ग संख्याएँ हैं :

{1, 4, 9, 16, 25, 36, 49, 64, 81} 1 से 90 तक 9 पूर्ण वर्ग संख्याएँ हैं।

पूर्ण वर्ग संख्या प्राप्त करने की प्रायिकता

P (एक पूर्ण वर्ग संख्या)

(iii) 5 से विभाज्य संख्याएँ हैं :

{5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90} 5 से विभाज्य 18 संख्याएँ हैं :

∴ 5 से विभाज्य संख्या प्राप्त करने की प्रायिकता

∴ अभीष्ट प्रायिकता

(i) A प्राप्त हो ? (ii) D प्राप्त हो ?

पासे के फलकों की संख्या = 6
S = {A, B, C, D, E, A}
n (S) = 6

(1) चूंकि दो फलकों पर A हैं।

∴ A प्राप्त करने की प्रायिकता

(2) चूँकि केवल एक फलक पर D अंकित है।

D प्राप्त करने की प्रायिकता

∴

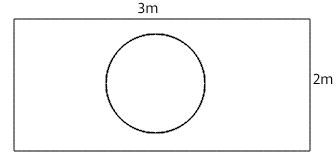
आयत की लंबाई (l) = 3 m
आयत की चौड़ाई (b) = 2 m
∴ आयत का क्षेत्रफल = 3 m x 2 m = 6 m²
वृत्त का व्यास = 1 m

वृत्त की त्रिज्या

∴ वृत्त का क्षेत्रफल = ????R²

पासे के वत्त के अंदर गिरने की प्रायिकता = वृत्त का क्षेत्रफल/ आयत का क्षेत्रफल

∴ अभीष्ट प्रायिकता

समूह में बॉल पेनों की कुल संख्या = 144
खराब पेनों की संख्या = 20
∴ अच्छे पेनों की संख्या = 144 – 20
= 124

(i) मान लीजिए आप वह पेन खरीदना चाहेंगे की घटना A है

∴ पेन खरीदने की प्रायिकता

(ii) आप वह पेन नहीं खरीदना चाहेंगे की घटना A होगी:

∴ P (पेन नहीं खरीदना चाहेंगे)

(i) निम्नलिखित सारणी को पूरा कीजिए :

घटना “दोनों पासों की संख्याओं का योग	प्रायिकता
2
3
4
5
6
7
8
9
10
11
12

(ii) एक विद्यार्थी यह तर्क देता है कि ‘यहाँ कुल 11 परिणाम 2, 3, 4, 5, 6, 7, 8, 9 10, 11 और 12 हैं। अतः, प्रत्येक की प्रायिकता
है।’ क्या आप इस तर्क से सहमत हैं? सकारण उत्तर दीजिए।
हल :जब दो पासे फेंके जाते हैं तो संभाव्य परिणाम हैं :

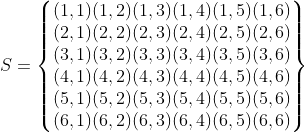
n(S) = 36

मान लीजिए ‘योग 3 प्राप्त करना’ घटना A है।

∴ A = {(1,2) (2,1)}

n (A) = 2

∴ योग 3 प्राप्त करने की प्रायिकता

मान लीजिए ‘योग 4 प्राप्त करना’ घटना B है

B = {(1, 3), (3, 1), (2, 2)}

n(B) = 3

∴

मान लीजिए ‘योग 5 प्राप्त करना’ घटना C है

C = {1,4) (4,1) (2, 3) (3, 2)}

n (C) = 4

∴

मान लीजिए ‘योग 6 प्राप्त करना’ घटना D है

D = {(1, 5) (5, 1) (2, 4) (4, 2) (3, 3)},

n(D) = 5

∴

मान लीजिए ‘योग 7 प्राप्त करना’ घटना E है

E = {(1, 6) (6, 1) (2, 5) (5, 2) (4, 3) (3, 4)}

∴ P (E) = P (योग 7 प्राप्त करना)

जब दोनो पासों को फेंका जाता हैं तो

मान लीजिए ‘योग 8 प्राप्त करना’ घटना F है

F = {(2, 6) (6, 2) (3, 5) (4, 4) (5, 3)}

∴ n (F) = 5

P (F) = P (योग 8 प्राप्त करना)

मान लीजिए ‘योग 9 प्राप्त करना’ घटना G है

G = {(4, 5) (5, 4) (3, 6) (6, 3)}

n(G) = 4

∴ P (G) = P (योग 9 प्राप्त करना)

मान लीजिए ‘योग 10 प्राप्त करना’ घटना H है

H = {(6, 4) (4, 6) (5, 5)}

n(H) = 3

∴ P (H) = P (योग 10 प्राप्त करना)

मान लीजिए ‘योग 11 प्राप्त करना’ घटना I है

I = {(5,6) (6, 5)}

n (I) = 2 ∴

मान लीजिए ‘योग 12 प्राप्त करना’ घटना J है

J = {(6, 6}; n (J) = 1 ∴

घटना दोनों पासों की संख्याओं का योग	प्रायिकता
2
3
4
5
6
7
8
9
10
11

(ii) नहीं सभी 11 संभाव्य परिणाम समप्रायिक नहीं हैं। क्योंकि उनकी प्रायिकता भिन्न-भिन्न है।

हल : जब एक रुपये के सिक्के को तीन बार उछाला जाता है तो संभाव्य परिणाम है :
S = {HHH, HHT HTH, THH, HTT, THT, TTH, TTT}
n (S) = 8

मान लीजिए तीनों परिणाम समान होना घटना A है अर्थात् {HHH, TTT}

∴

हार जाने की प्रायिकता = 1 – P (A)

∴ हार जाने की प्रायिकता

(i) 5 किसी भी बार में नहीं आएगा ?
(ii) 5 कम से कम एक बार आएगा ?

जब पासे को दो बार फेंका जाता है तो सभी संभाव्य परिणाम हैं :

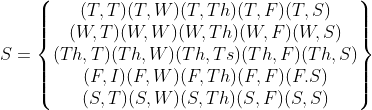
n (S) = 36

मान लीजिए ‘5 प्रत्येक बार 5 आएगा’ घटना A है

n (A) = 11

∴ 5 किसी भी बार नहीं आएगा’ घटना A है

n(A) = 36 – 11 = 25

(i) ∴ ‘5 किसी भी बार में नहीं आएगा’ की प्रायिकता

‘5 कम से कम एक बार आएगा’ की प्रायिकता

(i) यदि दो सिक्कों को एक साथ उछाला जाता है, तो इसके तीन संभावित परिणाम-दो चित, दो पट या प्रत्येक एक बार हैं। अतः,
इनमें से प्रत्येक परिणाम की प्रायिकता है।
(ii) यदि एक पासे को फेंका जाता है, तो इसके दो संभावित परिणाम एक विषम संख्या या एक सम संख्या हैं। अतः एक विषम संख्या ज्ञात करने की प्रायिकता हैं
हल :(i) जब दो सिक्कों को उछाला जाता है, तो संभाव्य परिणाम हैं :
S = {HH, HT, TH, TT}

दो चित प्राप्त करने की प्रायिकता

दो पट प्राप्त करने की प्रायिकता

एक चित और एक पट प्राप्त करने की प्रायिक प्रायिकता
∴ (i) तर्क असत्य है।

(ii) जब पासे को फेंका जाता है तो संभाव्य परिणाम हैं:

S = {1, 2, 3, 4, 5, 6}

n(S) = 6

विषम संख्याएँ हैं : 1, 3, 5

∴ विषम संख्या प्राप्त करने की प्रायिकता

सम संख्याएँ हैं : 2, 4, 6

∴ सम संख्या प्राप्त करने की प्रायिकता

(ii) तर्क सत्य है।

इस पोस्ट में आपको Class 10 Maths Chapter 15 Exercise 15.1 Solutions Class 10 maths chapter 15 exercise 15.1 probability NCERT Solutions for Class 10 Maths Chapter 15 Exercise 15.1 ncert class 10 maths chapter 15 pdf download Class 10 maths chapter 15 notes कक्षा 10 गणित अध्याय 15 प्रायिकता प्रश्नावली 15.1 कक्षा 10 गणित के लिए एनसीईआरटी समाधान अभ्यास 15.1 Class 10 Maths Solutions Chapter 15 प्रायिकता Ex 15.1 से संबंधित पूरी जानकारी दी गई है अगर इसके बारे में आपका कोई भी सवाल या सुझाव हो तो नीचे कमेंट करके हम से जरूर पूछें और अगर आपको यह जानकारी फायदेमंद लगे तो अपने दोस्तों के साथ शेयर जरूर करें.

NCERT Solutions for Class 10 Maths Chapter 15 प्रायिकता Exercise 15.1
NCERT Solutions for Class 10 Maths Chapter 15 प्रायिकता Exercise 15.2