Class 10 Maths Chapter 11 Exercise 11.2 – रचनाएँ

Class 10 Maths Chapter 11 Exercise 11.2 – रचनाएँ

NCERT Solutions for Class 10 Maths Chapter 11 Constructions Ex 11.2 – जो विद्यार्थी 10वीं कक्षा में पढ़ रहे है उनके लिए यहां पर एनसीईआरटी कक्षा 10 गणित अध्याय 11. (रचनाएँ) प्रश्नावली 11.2 के लिए सलूशन दिया गया है. जोकि एक सरल भाषा में दिया है .ताकि विद्यार्थी को पढने में कोई दिक्कत न आए .इसकी मदद से आप अपनी परीक्षा में अछे अंक प्राप्त कर सकते है. इसलिए निचे आपको एनसीईआरटी समाधान कक्षा 10 गणित अध्याय 11 रचनाएँ प्रश्नावली 11.2 दिया गया है .

NCERT Solutions For Class 10th Maths रचनाएँ (प्रश्नावली 11.2)

निम्न में से प्रत्येक के लिए रचना का औचित्य भी दीजिए :

हल :

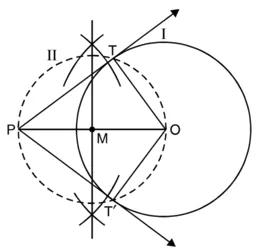
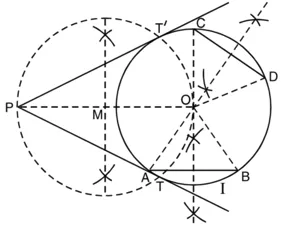
रचना के चरण :

1. बिंदु P को केंद्र तथा 6 cm त्रिज्या लेकर एक वृत्त (I) खींचिए।
2. केन्द्र से 10 cm की दूरी पर एक बिंदु 0 लीजिए। OP को मिलाइए।
3. OP का लंब समद्विभाजक खींचिए। मान लीजिए ‘M’, OP का मध्य बिंदु है।
4. ‘M’ को केन्द्र मानकर तथा MO त्रिज्या लेकर एक वृत्त (II) खींचिए जो कि वृत्त (I) को T और T’ पर प्रतिच्छेद करता है।
5. तब PT और PT’ अभीष्ट दो स्पर्श रेखाएँ हैं।

रचना का औचित्य :

हम जानते हैं कि किसी बिंदु पर स्पर्श रेखा उस बिंदु से खींची गई त्रिज्या पर लंब होती है। हमने सिद्ध करना है कि
∠PTO = ∠PT’O = 90°

OT को मिलाया गया है।
अब, PMO वृत्त (II) का व्यास है।
और ∠PTO अर्धवृत्त में है।

∴ ∠PTO = 90° [अर्धवृत्त में बना कोण समकोण होता है।]

इसी प्रकार, ∠PT’O = 90°

∴ PT और PT’ वृत्त की T और T’ पर स्पर्श रेखाएँ हैं।

स्पर्श रेखाओं की लंबाई मापने पर

अर्थात्, PT = 8.1 cm

PT’ = 8.1 cm

हल : संकेंद्रीय वृत्त : दो या अधिक वृत्त जिनका एक ही केन्द्र हो परंतु भिन्न भिन्न त्रिज्याएँ हों, संकेन्द्रीय वृत्त कहलाते हैं।

रचना के चरण :

1. एक वृत्त जिसका केन्द्र ‘O’ और त्रिज्या 4 cm हो खींचिए। इसे I अंकित कीजिए।

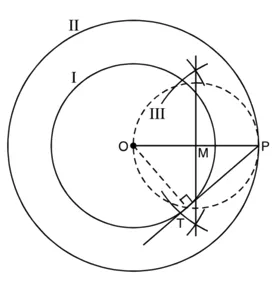
2. उसी केन्द्र ‘O’ से और त्रिज्या 6 cm का एक और वृत्त खींचिए, इसे II अंकित कीजिए।
3. वृत्त II पर कोई बिंदु ‘P’ लीजिए। OP को मिलाइए।
4. OP का लंब समद्विभाजक खींचिए। मान लीजिए यह ‘OP’ को M पर प्रतिच्छेद करता है।
5. M को केन्द्र मानकर और त्रिज्या ‘MO’ या ‘MP’, लेकर एक वृत्त III खींचिए जो वृत्त I को T और T” पर प्रतिच्छेद करे है।
6. PT को मिलाइए।
PT अभीष्ट स्पर्श रेखा है।

रचना का औचित्य :

OT को मिलाइए।
अब OP वृत्त III का व्यास है।
∠OTP अर्धवृत्त में बना कोण है।
∴ ∠OTP = 90°
अब OT ⊥ PT [(1) का प्रयोग करने पर]

∴ एक रेखा जो, वृत्त के किसी बिंदु पर त्रिज्या के साथ 90° का कोण बनाए, वह वृत्त पर स्पर्श रेखा होती है।

∴ PT वृत्त ‘I’ की स्पर्श रेखा है।
अर्थात् PT, 4 cm त्रिज्या वाले वृत्त पर स्पर्श रेखा है।
स्पर्श रेखा की लंबाई का परिकलन :

∆OTP लीजिए।

∠OTP = 90° [(1) का प्रयोग करने पर] ∴ ∆OTP एक समकोण त्रिभुज है।
OT = 4 cm [वृत्त I की त्रिज्या (दिया है)] OP = 6 cm [वृत्त II की त्रिज्या (दिया है)] PT = ? [परिकलित करना है]

समकोण ∆OTP में,

पाइथागोरस प्रमेय से,

OP² = OT² + PT² [(कर्ण)² = (आधार)² + (लंब)²]

या PT² = OP² – OT² = (6 cm)² – (4 cm)²
= 36 cm² – 16 cm² = 20 cm²
PT = √20 cm = 2√5 cm
= 2 x 2.24 cm = 4.48 cm.

इसलिए, परिकलन से स्पर्श रेखा की लंबाई

= 4.48 cm ≃ 4.5 cm

मापने पर स्पर्श रेखा की लंबाई

= 4.5 cm

अतः स्पर्श रेखा ‘PT’ की लंबाई सत्यापित है।

हल : रचना के चरण :

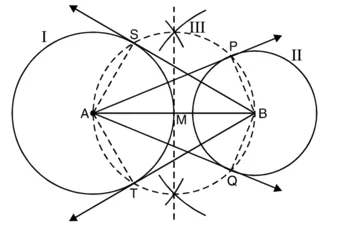
1. केन्द्र ‘O’ और त्रिज्या 3 cm का एक वृत्त खींचिए।
2. इसका व्यास ‘AB’ खींचिए और इसे दोनों दिशाओं में बढ़ाइए जैसे कि OX और OX’
3. ‘OX” पर बिंदु ‘P’ और ‘OX’ पर बिंदु ‘Q’ इस प्रकार लीजिए कि OP = OQ = 7 cm.

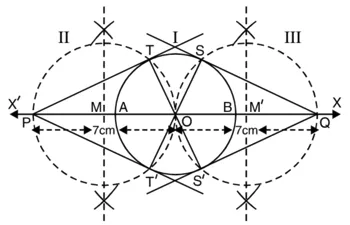
4. OP और OQ के लंब समद्विभाजक खींचिए जो OP और OQ को क्रमशः ‘M’ और ‘M” पर प्रतिच्छेद करें।
5. ‘M’ को केन्द्र मानकर और त्रिज्या = ‘MO’ या MP लेकर एक वृत्त II’ खींचिए जो वृत्त ‘I’ को T और T’ पर प्रतिच्छेद करे।
6. इसी प्रकार ‘M” को केन्द्र मानकर और M’O या M Q, को त्रिज्या लेकर वृत्त (III) खींचिए जो वृत्त ‘I’ को ‘S’ और ‘S’ पर प्रतिच्छेद करे।
7. PT, PT’ और OS तथा QS’ को मिलाइए।

रचना का औचित्य :

‘OT’ और ‘OT” तथा ‘OS’ और OS’ को मिलाइए।
PT और PT’ वृत्त की स्पर्श रेखाएँ हैं को सिद्ध करने के लिए हमें सिद्ध करना है कि
∠PTO = ∠PT’O = 90° है।
अब ‘OP’ वृत्त ‘II’ का व्यास है और ∠OTP अर्धवृत्त में बना कोण है।
∴ ∠OTP = 90° …(1)

[∵ अर्धवृत्त में बना कोण 90° का होता है।

परंतु ‘OT’ वृत्त ‘I’ की त्रिज्या है और रेखा ‘PT’ वृत्त को ‘T’ पर स्पर्श करती है।
∵ एक रेखा जो वृत्त को किसी बिंदु पर स्पर्श करती है और उस बिंदु पर त्रिज्या के साथ 90° का कोण बनाती है, वृत्त की स्पर्श रेखा होती है।
∴ PT वृत्त I की बिंदु T पर बिंदु ‘P’ से स्पर्श रेखा है।
इसी तरह PT’, QS और OS’ वृत्त I पर स्पर्श रेखाएँ हैं।

हल : रचना के चरण :

1. अभीष्ट आकृति का कच्चा खाका खींचिए।

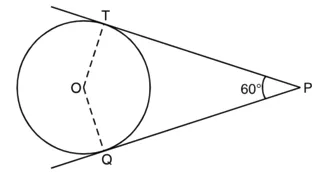
∵ स्पर्श रेखाएँ परस्पर 60° का कोण बनाती हैं।
∠OTP = ∠OQT = 90°
[स्पर्श रेखा वृत्त की त्रिज्या पर लंब है।] त्रिज्याओं का परस्पर झुकाव ज्ञात करना कि
∠TOQ + ∠OTP + ∠OOT + ∠TPQ = 360°
[चतुर्भुज का कोण योग गुण] या ∠TOQ° + 90° + 90° + 60° = 360°
या ∠TOQ = 360° – 90° – 90° – 60° = 120°

2. 5 cm त्रिज्या का एक वृत्त खींचिए।
3. इस वृत्त की दो त्रिज्याएँ खींचिए जो परस्पर 120° का कोण बनाएं।
4. मान लो, त्रिज्याएं वृत्त को ‘A’ और ‘B’ पर प्रतिच्छेद करती हैं।
5. A और B पर 90° का कोण बनाएं जो परस्पर ‘P’ पर प्रतिच्छेद करें।

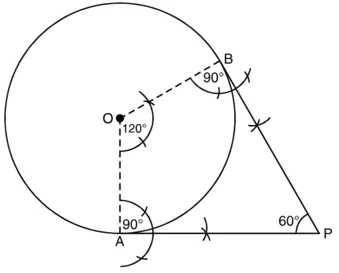
6. PA और PB अभीष्ट स्पर्श रेखाएँ हैं।

हल :

रचना के चरण :

1. एक रेखाखंड AB = 8 cm खींचिए।
2. ‘A’ को केन्द्र मानकर और त्रिज्या 4 cm लेकर वृत्त (I) खींचिए।
3. ‘B’ को केन्द्र मानकर और त्रिज्या 3 cm लेकर वृत्त ‘II’ खींचिए।
4. रेखाखंड AB का लंब समद्विभाजक खींचिए जो ‘AB’ को ‘M’ पर प्रतिच्छेद करे।
5. ‘M’ को केन्द्र मानकर और त्रिज्या MA या MB लेकर वृत्त (III) खींचिए जो वृत्त (I) को ‘S’ और ‘T’ पर और वृत्त (II) को ‘P’ और ‘Q’ पर प्रतिच्छेद करे।
6. ‘AP’ और ‘AQ’ को मिलाइए। ये बिंदु ‘A’ से 3 cm त्रिज्या वाले वृत्त की अभीष्ट स्पर्श रेखाएँ हैं।
7. ‘BS’ और ‘BT’ को मिलाइए। ये बिंदु ‘B’ से 4 cm त्रिज्या वाले वृत्त की अभीष्ट स्पर्श रेखाएं हैं।

रचना का औचित्य :

वृत्त (III) में, AB व्यास है, तथा ∠ASB और ∠BPA अर्धवृत्त में बने कोण हैं।
∴ ∠ASB = 90° [अर्धवृत्त में बना कोण]…(1)
और ∠BPA = 90° [ ” ] …(2)
परंतु ∠ASB त्रिज्या और रेखाखंड ‘BS’ के बीच का कोण है और ∠BPA त्रिज्या और रेखाखंड AP’ के बीच का कोण है।
∵ रेखा जो वृत्त की त्रिज्या पर लंब है, उस बिंदु पर वृत्त की स्पर्श रेखा होती है।
∴ BS वृत्त (I) की बिंदु ‘S’ पर स्पर्श रेखा है और AP वृत्त (II) की बिंदु ‘P’ पर स्पर्श रेखा है।
इसी प्रकार, AQ और BT क्रमशः वृत्त (II) और (I) की स्पर्श रेखाएं हैं।

हल:

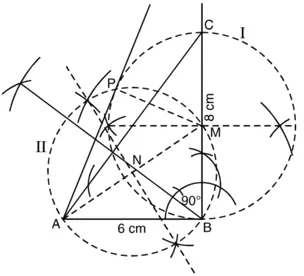
रचना के चरण :

1. समकोण त्रिभुज ABC की रचना दी गई शर्तों और माप के साथ कीजिए।
2. BD ⊥ AC खींचिए।
3. भुजा BC का मध्य बिंदु ‘M’ लीजिए।
4. ‘M’ को केन्द्र और BC को व्यास मानकर, B, C, D में से, एक वृत्त खींचिए। इसे वृत्त I लीजिए।
5. ‘A’ और ‘M’ को मिलाइए।
6. AM का लंब समद्विभाजक खींचिए जो AM को ‘N’ पर प्रतिच्छेद करे। ‘N’ को केन्द्र और ‘NA’ या ‘NM’ त्रिज्या लेकर एक वृत्त (II) खींचिए जो वृत्त (I) को ‘B’ और ‘P’ पर प्रतिच्छेद करे।
7. AP को मिलाइए।
8. AP और AB अभीष्ट स्पर्श रेखाएँ हैं।

रचना का औचित्य :

रेखाखंड ‘AM’ को व्यास लेकर वृत्त (III) खींचिए।
∠APM अर्धवृत्त में बना कोण है।
∴ ∠APM = 90° [अर्धवृत्त में कोण]

अर्थात् MP ⊥ AP

परंतु ‘MP’ वृत्त (I) की त्रिज्या है।
∴ AP वृत्त (I) की स्पर्श रेखा है।
[∵ वृत्त के किसी बिंदु पर वृत्त की त्रिज्या पर लंब कोई रेखा उस वृत्त की स्पर्श रेखा होती है।] इसी प्रकार ‘AB’ वृत्त (I) की स्पर्श रेखा है।

हल : किसी चूड़ी की सहायता से वृत्त खींचने का अर्थ है कि वृत्त का केन्द्र अज्ञात है। सर्वप्रथम हम केन्द्र ज्ञात करेंगे।

रचना के चरण :

1. चूड़ी की सहायता से वृत्त (I) खींचिए।
2. वृत्त की कोई दो जीवाएँ AB और CD (समांतर नहीं) खींचिए।
3. जीवा AB और CD के लंब समद्विभाजक खींचिए जो परस्पर प्रतिच्छेद करें।
[∵ रेखाखंड के लंब समद्विभाजक पर स्थित कोई बिंद इसके अंत बिंदुओं से समदूरस्थ होता है।
[∵ ‘O’, AB और CD के लंब समद्विभाजक पर स्थित है।] ∴ OA = OB और OC = OD
∴ OA = OB = OC = OD (वृत्त की त्रिज्याएँ)
∴ ‘O’ वृत्त का केन्द्र है।

4. वृत्त के बाहर कोई बिंदु ‘P’ लीजिए।
5. OP को मिलाइए।
6. OP का लंब समद्विभाजक खींजिए। मान लीजिए ‘M’, OP का मध्य बिंदु है।
7. ‘M’ को केन्द्र और त्रिज्या ‘MP’ या ‘MO’ लेकर एक वृत्त II खींचिए जो वृत्त (I) को T और T’ पर प्रतिच्छेद करे।
8. PT और PT’ को मिलाइए जो कि अभीष्ट स्पर्श रेखाओं का युग्म है।

रचना का औचित्य :

हमने सिद्ध करना है कि
∠PTO = PT’O = 90°
OT को मिलाइए।
अब ∠PTO अर्धवृत I में हैं।
∴ ∠PTO = 90° [अर्धवृत्त में बना कोण समकोण होता है] इसी तरह, ∠PTO = 90°
∴ PT और PT’ वृत पर बिन्दुओं T और T’ पर क्रमशः स्पर्श रेखाएं हैं।

इस पोस्ट में आपको Class 10 Maths Chapter 11 रचनाएँ प्रश्नावली 11.2 Class 10 Maths Chapter 11 Compositions NCERT Solutions for Chapter 11 Maths Class 10 Constructions Exercise 11.2 Class 10 Maths Chapter 11 Exercise 11.2 एनसीईआरटी समाधान कक्षा 10 गणित अध्याय 11 अभ्यास 11.2 Class 10th Maths Solutions Chapter 11 रचनाएँ Class 10 Maths रचनाएँ प्रश्नावली 11.2 से संबंधित पूरी जानकारी दी गई है अगर इसके बारे में आपका कोई भी सवाल या सुझाव हो तो नीचे कमेंट करके हम से जरूर पूछें और अगर आपको यह जानकारी फायदेमंद लगे तो अपने दोस्तों के साथ शेयर जरूर करें.

NCERT Solutions for Class 10 Maths Chapter 11 रचनाएँ Exercise 11.1
NCERT Solutions for Class 10 Maths Chapter 11 रचनाएँ Exercise 11.2