Class 10 Maths Chapter 11 Exercise 11.1 – रचनाएँ

Class 10 Maths Chapter 11 Exercise 11.1 – रचनाएँ

NCERT Solutions for Class 10 Maths Chapter 11 Constructions Ex 11.1 – आज हम आप के लिए Class 10 Maths Chapter 11 Constructions में लेकर आयें है। जो कि Class 10 Maths Exams के लिए अत्यन्त उपयोगी साबित होगी. कक्षा 10वीं के विद्यार्थी के लिए यहां पर एनसीईआरटी कक्षा 10 गणित अध्याय 11. (रचनाएँ) प्रश्नावली 11.1 के लिए सलूशन दिया गया है. जोकि एक सरल भाषा में दिया है .ताकि विद्यार्थी को पढने में कोई दिक्कत न आए .इसकी मदद से आप अपनी परीक्षा में अछे अंक प्राप्त कर सकते है.

NCERT Solutions For Class 10th Maths रचनाएँ (प्रश्नावली 11.1)

निम्न में से प्रत्येक के लिए रचना का औचित्य भी दीजिए :

रचना के चरण :

1. एक रेखाखंड AB = 7.6 cm लीजिए।
2. न्यून ZBAX बनाती हुई कोई किरण AX खींचिए।
3. किरण AX पर 5 + 8 = 13 (दिया गया अनुपात 5 : 8) बिन्दु A₁, A₂, A₃, A₄, A₅………A₁₀, A₁₁, A₁₂, A₁₃ इस प्रकार अंकित कीजिए कि AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = ….. = A₁₁A₁₂ = A₁₂ A₁₃ हो।
4. BA₁₃ को मिलाइए।
5. बिंदु A₅, से होकर जाने वाली A₅C || A₁₃B (A₅ पर ∠AA₁₃B
के बराबर कोण बनाकर) AB को एक बिंदु ‘C’ प्रतिच्छेद करती हुई खींचिए। तब AC : CB = 5 : 8

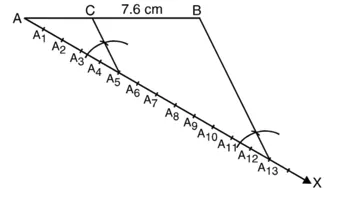
औचित्य : आइए हम देखें कि यह विधि कैसे हमें अभीष्ट विभाजन प्रदान करती है। ∆AA₁₃B में,

∵ A₅C || A₁₃B है।

∴ आधारभूत समानुपातिकता प्रमेय द्वारा

रचना से,

∴

यह दर्शाता है कि ‘C’, AB को 5 : 8 के अनुपात में विभाजित करता है। दोनों भागों को मापने पर,
AC = 2.9 cm, CB = 4.7 cm

वैकल्पिक विधि :

रचना के चरण :

1. एक रेखाखंड AB = 7.6 cm लीजिए।
2. एक न्यून कोण BAX खींचिए।
3. ∠ABY इस प्रकार खींचिए कि
∠ABY = BAX हो

4. बिंदु A₁, A₂, A₃, A₄, A₅ किरण AX पर अंकित कीजिए ताकि AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅.

5. बिंदु B₁, B₂, B₃, B₄, B₅, B₆, B₇, B₈ किरण BY पर इस प्रकार अंकित कीजिए कि

BB₁ = B₁B₂ = B₂B₃ = B₃B₄
= B₄B₅ = B₅B₆ = B₆B₇ = B₇B₈
6. A₅B₈ को मिलाइए मानो यह AB को बिंदु ‘C’ पर प्रतिच्छेद करती है। तब AC : CB = 5 : 8

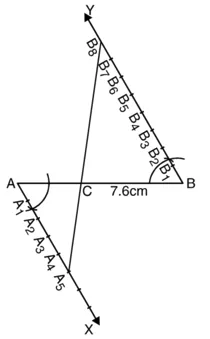
औचित्य :
∆ACA₅, और ∆ BCB₈ में,
∠ACA₅ = ∠BCB₈ [शीर्षाभिमुख कोण] ∠ABB₈ = ∠BAA₈ [रचना] ∴ ∆ACA₈ ~ ∆BCB₈ [AA-समरूपता कसौटी]

∴ त्रिभुजों की संगत भुजाएँ एक ही अनुपात में होंगी।

(I) (II) (III)

I और III से,

परन्तु

⇒

अत: AC : CB = 5 : 8

प्रश्न 2. 4 cm, 5 cm और 6 cm भुजाओं वाले एक त्रिभुज की रचना कीजिए और फिर इसके समरूप एक अन्य त्रिभुज की रचना कीजिए जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की गुनी हों।

1. दी गई शर्तों और मापों से एक त्रिभुज की रचना कीजिए। मान लीजिए ∆ABC है। ∆ABC में, AB = 5 cm,
AC = 4 cm और BC = 6 cm.
2. भुजा BC के नीचे कोई कोण ∠CBX बनाइए।

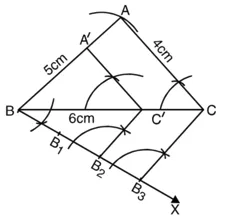
3. तीन बिंदु ( में 2 और 3 में से बड़ी संख्या) B₁, B₂, B₃, BX पर इस प्रकार अंकित कीजिए कि BB₁ = B₁B₂ = B₂B₃ हो।

4. B₃BC को मिलाइए।

5. B₂, ( में 2 और 3 में से छोटी संख्या) में से एक रेखा B₃C के समांतर खींचिए जो BC को C’ पर प्रतिच्छेद करती है। 6. C’, में से होकर

जाने वाली CA के समांतर एक रेखा खींचिए जो BA को A’ पर मिले।

अतः, ∆A’BC’ अभीष्ट त्रिभुज है जिसकी भुजाएँ ∆ABC की संगत भुजाओं की गुनी हैं।

रचना का औचित्य :

पहले हम यह दिखाएंगे कि पहली त्रिभुज और रचना की गई त्रिभुज समरूप हैं।
अर्थात् ∆A’BC’ ~ ∆ABC.
∆A’BC’ और ∆ABC में
∠B = ∠B [उभयनिष्ठ] ∠A’C’B = ∠ACB [रचना से] ∆A’C’B ~ ∆ACB [AA-समरूपता]

∴ त्रिभुजों की संगत भुजाएँ समान अनुपात में होंगी।

…(1)

अब ∆B₂BC’ और ∆B₃BC लीजिए

∠B = ∠B [उभयनिष्ठ]

BB₂C’ = BB₃C [रचना]

∴ BB₂C’ = BB₂C [AA – समरूप]

∴ त्रिभुजों की संगत भुजाएँ समान अनुपात में होंगी।

अर्थात्

I II III

(I) और (II) को लेने पर,

परन्तु (रचना)

……(2)

(1) और (2) से,

⇒

और

अतः, रचना औचित्य पूर्ण है।

प्रश्न 3. 5 cm, 6 cm और 7 cm भुजाओं वाले एक त्रिभुज की रचना कीजिए और फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिये हुए त्रिभुज की संगत भुजाओं की गुनी हों।

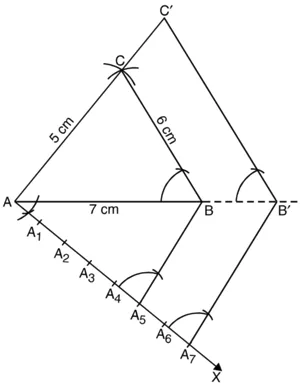
रचना के चरण :

1. ∆ABC की रचना कीजिए जिसमें AB = 7 cm, BC = 6 cm और AC = 5 cm हैं।
2. आधार AB के नीचे कोई न्यून कोण ∠BAX बनाइए।
3. सात बिंदु A₁, A₂, A₃, A₄, A₅, A₆, A₇, किरण AX पर इस प्रकार अंकित कीजिए कि

AA₁ = A₁A₂ = A₂A₃ = A₃A₄
= AA; = A-A6 = A6A, हो।
4. BA₅ को मिलाइए।

5. A₇, से A₅B के समांतर एक रेखा खींचिए। मान लीजिए यह AB को बढ़ाने पर B’ पर इस प्रकार मिलती है कि

6. B’ में से BC के समांतर एक रेखा खींचिए जो AC को बढ़ाने पर C’ पर मिलती है।

रचना का औचित्य

∆ABC और ∆AB’C’ में,

∠A = ∠A [उभयनिष्ठ]

∠ABC = ∠AB’C’ [रचना] ∴ ∆ABC ~ ∆AB’C’ [AA-समरूपता]

∴ त्रिभुजों की संगत भुजाएँ एक ही अनुपात में होंगी।

….(1)

पुनः ∆AA₅B और ∆AA₇B’ में,

∠A = ∠A [उभयनिष्ठ]

∠AA₅B = ∠AA₇B’ [रचना]

∴ ∆AA₅B ~ ∆AA₇B’ [AA – समरूपता]

∴ त्रिभुजों की संगत भुजाएँ एक ही अनुपात में होंगी।

⇒

परंतु, [रचना]

⇒ …(2)

(1) और (2) से,

या

⇒

और

अत: ∆AB’C’ की भुजाएँ ∆ABC की संगत भुजाओं की गुनी हैं।

प्रश्न 4. आधार 8 cm तथा ऊँचाई 4 cm के एक समद्विबाहु त्रिभुज की रचना कीजिए और फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ इस समद्विबाहु त्रिभुज की संगत भुजाओं की गुनी हों

रचना करना : एक त्रिभुज जिसकी भुजाएँ समद्विबाहु त्रिभुज की संगत भुजाओं का गुनी हैं।

रचना के चरण :

1. आधार AB = 8 cm लीजिए।
2. AB का लंब समद्विभाजक खींचिए जो AB को ‘M’ पर प्रतिच्छेद करे।
3. M को केन्द्र मानकर और त्रिज्या 4 cm, लेकर एक चाप लगाइए जो लंब समद्विभाजक को ‘C’ पर प्रतिच्छेद करे।
4. CA और CB को मिलाइए।
5. ∆ABC समद्विबाहु त्रिभुज है जिसमें CA = CB.
6. भुजा BC के नीचे कोई न्यून कोण ZBAX बनाइए।

7. तीन बिंदु ( या में तथा 3 में से बड़ी संख्या) A₁, A₂, A₃, ‘AX’ पर इस प्रकार अंकित कीजिए कि AA₁ = A₁A₂ = A₂A₃ हो।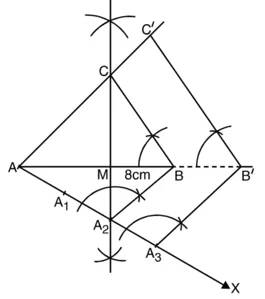

8. A₂ ( में ‘2’ और ‘3’ में से छोटी संख्या) और B को मिलाइए।

9. A₃, में से एक रेखा A₂B के समांतर खींचिए जो AB को बढ़ाने पर B’ पर मिले।
10. B’, में से एक रेखा BC के समांतर खींचिए जो AC को बढ़ाने पर C’ पर मिले। ∆AB’C’ अभीष्ट त्रिभुज है जिसकी भुजाएँ ∆ABC की संगत भुजाओं की गुनी हैं।

रचना का औचित्य :

सर्वप्रथम हम सिद्ध करेंगे कि ∆AB’C’ और ∆ABC समरूप हैं। ∆AB’C’ और ∆ABC में,
∠A = ∠A [उभयनिष्ठ]∠AB’C’ = ∠ABC [रचना से]∆AB’C’ ~ ∆ABC [AA-समरूपता से

∴ त्रिभुजों की संगत भुजाएँ एक ही अनुपात में हैं।

….(1)

अब ∆ A₃AB’ और ∆ A₂AB में,

∠A = ∠A [उभयनिष्ठ]

∠B’A₃A = ∠BA₂A [रचना से]

∴ ∆A₃AB’ ~ ∆A₂AB [AA-समरूपता]

∴ त्रिभुजों की संगत भुजाएँ एक ही अनुपात में होंगी।

I II III

(I) और (II) को लेने पर,

परंतु,

⇒ …..(2)

(1) और (2) से,

⇒

⇒

और

अत: रचना औचित्य पूर्ण है।

प्रश्न 5. एक त्रिभुज ABC बनाइए जिसमें BC = 6 cm, AB = 5 cmऔर ∠ABC = 60° हो। फिर एक त्रिभुज की रचना कीजिए, जिसकी भुजाएँ ∆ABC की संगत भुजाओं की गुनी हों।

1. रेखाखंड BC = 6 cm लीजिए।
2. B पर 60° का कोण बनाइए अर्थात् ∠BAX = 60° बनाइए।
3. B को केन्द्र मानकर और 5 cm त्रिज्या लेकर एक चाप खींचिए जो BX को ‘A’ पर प्रतिच्छेद करे।

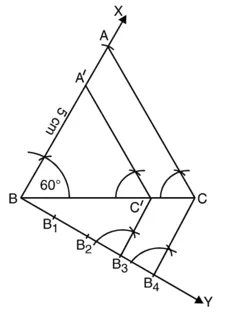
4. A और C को मिलाइए।
5. BC के नीचे B पर कोई न्यून कोण बनाइए।

6. चार बिंदु ( में 3 और 4 में से बड़ी संख्या) B₁ B₂, B₃, B₄, रेखा BY पर इस प्रकार अंकित कीजिए कि BB₁, = B₁B₂ = B₂B₃ = B₃B₄ हो।
7. B₄ और C को मिलाइए।

8. B₃ ( में 3 और 4 से छोटी संख्या) में से एक रेखा B₄C के समांतर खींचिए। मान लीजिए B₃, में से खींची रेखा BC को C’ पर प्रतिच्छेद करती है।
9. C’, में से एक रेखा CA के समांतर खींचिए जो BA को A’ पर प्रतिच्छेद करती है।

∆A’BC’ अभीष्ट त्रिभुज है जिसकी संगत भुजाएँ ∆ABC की संगत भुजाओं के गुनी हैं।

रचना का औचित्य :

∆A’BC’ और ∆ABC लीजिए।
∠B = ∠B [उभयनिष्ठ] ∠A’C’B = ∠ACB [संगत कोण] ∴ ∆ABC ~ ∆ABC [AA-समरूपता] ∴ त्रिभुजों की संगत भुजाएँ एक ही अनुपात में होंगी।

∴ …..(1)

अब ∆B₃BC’ और ∆B₄BC में,

∠B = ∠B [उभयनिष्ठ]

∠C’B₃B = ∠CB₄B [संगत कोण

∆B₄BC’ ~ ∆B₄BC [AA-समरूपता]

∴ त्रिभुजों की संगत भुजाएँ एक ही अनुपात में होंगी।

….(2)

(I) और (II) से,

परंतु, [रचना]

…(3)

(1) और (3) से,

⇒

और

अर्थात् ∆A’BC’ की भुजाएँ ∆ABC की संगत भुजाओं की गुनी हैं।

प्रश्न 6. एक त्रिभुज ABC बनाइए, जिसमें BC = 7 cm, ∠B = 45°, ∠A = 105° हो। फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ ∆ABC की संगत भुजाओं की गुनी हों।

1. दिए गए मापों से त्रिभुज ABC की रचना कीजिए।
2. भुजा BC के नीचे बिंदु B पर कोई न्यून कोण CBX खींचिए।

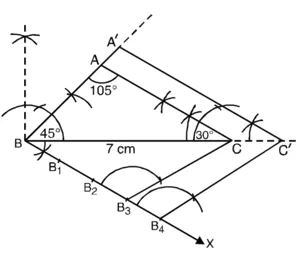
त्रिभुज के कोण योग गुणधर्म से

∠A + ∠B + ∠C = 180°
105° + 45° + ∠C = 180°
∠C = 180° – 150° = 30°
3. चार बिंदु ( में 3 और 4 में से बड़ी संख्या) B₁, B₂, B₃, B₄, ‘BX’ पर इस प्रकार अंकित कीजिए कि BB₁ = B₁B₂ = B₂B₃ = B₃B₄ हो।

4. B₃C ( में 3 और 4 में से छोटी) को मिलाइए।

5. B₄ में से एक रेखा B₃C के समांतर खींचिए जो BC को बढ़ाने पर C’ पर प्रतिच्छेद करे।
6. C’ में से एक अन्य रेखा CA के समांतर खींचिए जो BA को बढ़ाने पर A’ पर प्रतिच्छेद करे।
7. ∆ A’BC’ अभीष्ट त्रिभुज है जिसकी भुजाएँ त्रिभुज ABC की संगत भुजाओं की गुनी हैं।

रचना का औचित्य :

∆ABC’ और ∆ ABC में,
∠B = ∠B [उभयनिष्ठ
∠A’C’B = ∠ACB [रचना] ∴ ∆ABC ~ ∆ABC [AA-समरूपता] ∴ त्रिभुजों की संगत भुजाएँ एक ही अनुपात में होंगी।

…(1)

पुन: ∆B₄BC’ और ∆B₃BC लीजिए।

∠B = ∠B [उभयनिष्ठ]

∠C’B₄B = ∠CB₃B [रचना से]

∴ ∆B₄BC’ ~ ∆B₃BC [AA – समरूपता]

∴ त्रिभुजों की संगत भुजाएँ एक ही अनुपात में होंगी।

I II III

I और II लेने पर,

परन्तु, (रचना)

इसलिए …(2)

(1) और (2) से,

⇒

और

अतः रचना का औचित्य पूर्ण है।

प्रश्न 7. एक समकोण त्रिभुज की रचना कीजिए, जिसकी भुजाएँ (कर्ण के अतिरिक्त) 4 cm तथा 3 cm लंबाई की हों। फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की गुनी हों।

1. दी गई शर्तों से समकोण त्रिभुज खींचिए। मान लीजिए यह ∆ABC है। BC = 4 cm; AB = 3 cm और ∠B = 90°
2. भुजा BC के नीचे कोई न्यून कोण CBX खींचिए।

3. पाँच बिंदु ( में 5 और 3 में से बड़ी संख्या) B₁, B₂, B₃, B₄, B₅, BX पर इस प्रकार अंकित कीजिए कि BB₁ = B₁B₂ = B₂ B₃ = B₃B₄ = B₄B₅ हो।

4. B₃ ( में ‘5’ और ‘3’ से छोटी संख्या) और ‘C’ को मिलाइए।

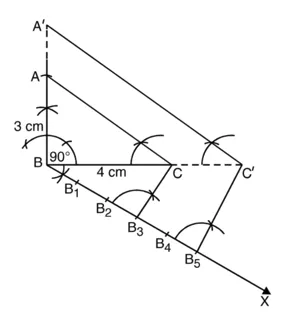
5. B₅ में से एक रेखा BC के समांतर खींचिए जो BC को बढ़ाने पर C’ पर प्रतिच्छेद करे।
6. पुन: C’ में से एक रेखा CA के समांतर खींचिए जो BA को बढ़ाने पर
A’ पर मिले। ∆’ABC’ अभीष्ट त्रिभुज है जिसकी भुजाएँ ∆ABC की संगत भुजाओं की गुनी हैं।

रचना का औचित्य :

∆ABC’ और ∆ABC में,
∠B = ∠B [उभयनिष्ठ] ∠A’C’B = ∠ACB [रचना से] ∴ ∆A’BC’ = ∆ABC [AA-समरूपता कसौटी] ∴ त्रिभुजों की संगत भुजाएँ एक ही अनुपात में हैं।

अर्थात्

पुन: ∆B₅C’ B और ∆B₅CB में,

∠B = ∠B [उभयनिष्ठ]

∠C’B₅B = ∠CB₃B [रचना से]

∴ ∆B₅C’B ~ ∆B₃CB [AA-समरूपता]

∴ त्रिभुजों की संगत भुजाएँ एक ही अनुपात में हैं।

I II III

II और III को लेने पर,

परंत,

⇒ …(2)

(1) और (2) से,

⇒

और

अतः रचना का औचित्य पूर्ण है।

इस पोस्ट में आपको NCERT Solutions for Class 10 Maths Exercise 11.1 Construction class 10 maths chapter 11 solutions pdf Class 10 Maths Chapter 11 Exercise 11.1 एनसीईआरटी समाधान कक्षा 10 गणित प्रश्नावली 11.1 कक्षा 10 गणित रचनाएँ प्रश्नावली 11.1 Class 10 Maths Chapter 11 रचनाएँ Ex 11.1 से संबंधित पूरी जानकारी दी गई है अगर इसके बारे में आपका कोई भी सवाल या सुझाव हो तो नीचे कमेंट करके हम से जरूर पूछें और अगर आपको यह जानकारी फायदेमंद लगे तो अपने दोस्तों के साथ शेयर जरूर करें.

NCERT Solutions for Class 10 Maths Chapter 11 रचनाएँ Exercise 11.1
NCERT Solutions for Class 10 Maths Chapter 11 रचनाएँ Exercise 11.2