NCERT Solutions for Class 10 Maths Chapter 10 – वृत्त

NCERT Solutions for Class 10 Maths Chapter 10 – वृत्त

NCERT Solutions Class 10 Maths Chapter 10 वृत्त – ऐसे छात्र जो कक्षा 10 गणित विषय की परीक्षाओं में अच्छे अंक प्राप्त करना चाहते है उनके लिए यहां पर एनसीईआरटी कक्षा 10th गणित अध्याय 5 (वृत्त) के लिए सलूशन दिया गया है. यह जो NCERT Solution For Class 10 Maths Chapter 10 Circles दिया गया है वह आसन भाषा में दिया है .ताकि विद्यार्थी को पढने में कोई दिक्कत न आए . इसकी मदद से आप अपनी परीक्षा में अछे अंक प्राप्त कर सकते है.इसलिए आप Class 10 Maths Chapter 10 वृत्त के प्रश्न उत्तरों को ध्यान से पढिए ,यह आपके लिए फायदेमंद होंगे.

NCERT Solutions For Class 10th Maths वृत्त (प्रश्नावली 10.1)

हल :क्योंकि वृत्त के किसी बिंदु पर एक व केवल एक ही स्पर्श रेखा हो सकती है। परंतु वृत्त एक अनंत बिंदुओं का समूह होता है।इसलिए हम वृत्त पर अनंत स्पर्श रेखाएं खींच सकते हैं।

(i) किसी वृत्त की स्पर्श रेखा उसे ……. बिंदु पर प्रतिच्छेद करती है।
(ii) वृत्त को दो बिंदुओं पर प्रतिच्छेद करने वाली रेखा को…….कहते हैं। (iii) एक वृत्त की…….समांतर स्पर्श रेखाएँ हो सकती हैं।
(iv) वृत्त तथा उसकी स्पर्श रेखा के उभयनिष्ठ बिंदु को ……. कहते हैं।

हल :(i) किसी वृत्त की स्पर्श रेखा उसे एक बिंदु पर प्रतिच्छेद करती है।
(ii) वृत्त को दो बिंदुओं पर प्रतिच्छेद करने वाली रेखा को छेदक रेखा कहते हैं। (iii) एक वृत्त की दो समांतर स्पर्श रेखाएं हो सकती हैं।
(iv) वृत्त तथा उसकी स्पर्श रेखा के उभयनिष्ठ बिंदु को स्पर्श बिंदु कहते हैं।

(a) 12 cm
(b) 13 cm
(c) 8.5 cm
(d) √119 cm

हल :दी गई सूचना के अनुसार हम आकृति खींचते हैं जिससे कि

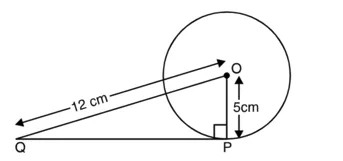
OP = 5 cm और OQ = 12 cm
∵ PQ एक स्पर्श रेखा है और OP त्रिज्या है।
∴ ∠OPQ = 90°

अब, समकोण ∆ OPQ में,

पाइथागोरस प्रमेय से

OQ² = OP² + OP²
या (12 cm)² = (5 cm)² + OP²
या QP² = (12 cm)² – (5 cm)²
या QP² = 144 cm² – 25 cm² = 119 cm²
या QP = √119 cm
अतः, विकल्प (d) सही है उत्तर

हल :दी गई सूचना के अनुसार हम एक वृत्त खींचते हैं जिसका केंद्र O और l दी गई रेखा हो।
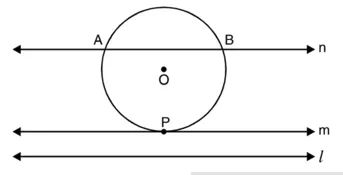
अब, m और n दो ऐसी रेखाएं हैं जो रेखा l के इस तरह समांतर हैं कि m स्पर्श रेखा भी है और l के समांतर भी है और n वृत्त की एक छेदक रेखा भी है और l के समांतर भी।

NCERT Solutions For Class 10th Maths वृत्त (प्रश्नावली 10.2)

प्रश्न सं. 1, 2, 3 में सही विकल्प चुनिए एवं उचित कारण दीजिए।

(a) 7 cm (b) 12 cm
(c) 15 cm (d) 24.5 cm

हल : एक वृत्त जिसका केंद्र O है। बाह्य बिंदु Q से स्पर्श रेखा PQ की लंबाई 24 cm तथा Q की केंद्र 0 से दूरी 25 cm है।

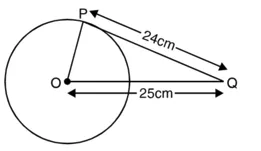
∴ ∠QPO = 90°

अब, समकोण ∆OPQ में,

OQ² = PQ² + OP²
(25 cm)² = (24 cm)² + OP²
या 625 cm² = 576 cm² + OP²
या OP² = 625 cm² – 576 cm²
या OP² = 49 cm² = (7 cm)²
या OP = 7 cm

∴ विकल्प (a) सही है। उत्तर

(a) 60° (b) 700
(c) 80° (d) 90°

हल : आकृति में OP त्रिज्या है और PT वृत्त पर स्पर्श रेखा है।

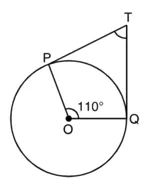
∴ ∠OPT = 90°

इसी तरह ∠OQT = 90° और ∠POQ = 110° (दिया है)

अब POQT एक चतुर्भुज है,

∴ ∠POQ + ∠OOT + ∠PTQ + ∠TPO = 360°
110° + 90° + ∠OTP + 90° = 360°
या ∠OTP + 290° = 360°
या ∠PTQ = 360° – 290°
या ∠PTQ = 70°
∴ विकल्प (b) सही है। उत्तर

(a) 50° (b) 60°
(c) 70° (d) 80°

हल :दी गई आकृति में OA त्रिज्या है और AP वृत्त पर स्पर्श रेखा है।

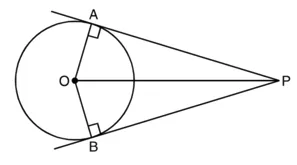
∴ ∠OAP = 90°

इसी प्रकार, ∠OBP = 90°

अब समकोण ∆PAO और ∆PBO में,

∠PAO = ∠PBO = 90°
OP = OP (उभयनिष्ठ भुजा)
OA = OB (एक ही वृत्त की त्रिज्याएँ)
∴ ∆PAO ≅ ∆PBO [RHS सर्वांगसमता] ∴ ∠AOP = ∠BOP [सर्वांगसम त्रिभुजों के संगत अंश] या ∠AOP = ∠BOP [सर्वांगसम त्रिभुजों के संगत अंश]

…(1)

साथ ही, चतुर्भुज OAPB में,

∠OBP + ∠BPA + ∠OAP + ∠AOB = 360°
90° + 80° + 90° + ∠AOB = 360°
∠AOB = 360° – 260°
∠AOB = 100° …..(2)

(1) और (2) से, हमें प्राप्त होता है

∠AOP = ∠BOP

∴ विकल्प (α) सही है। उत्तर

हल : दिया है : एक वृत्त जिसका केंद्र O तथा व्यास AB है। l और m बिंदु A
और B पर स्पर्श रेखाएँ हैं।

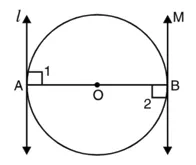
सिद्ध करना है : l || m

उपपत्ति ∴ OA त्रिज्या है और l वृत्त पर स्पर्श रेखा है।

∴ ∠1 = 90°
इसी प्रकार, ∠2 = 90°
अब, ∠1 = ∠2 = 90°

परंतु यह दो रेखाओं के एकांतर कोण हैं, जब एक तिर्यक रेखा उन्हें काटती है।

∴ l || m

अतः, किसी व्यास के सिरों पर खींची गई स्पर्श रेखाएँ परस्पर समांतर होती हैं।

हल : दिया है :एक वृत्त जिसका केंद्र O है। AB इसकी स्पर्श रेखा है जो वृत्त
को P पर मिलती है।
अर्थात् बिंदु P वृत्त का स्पर्श बिंदु है

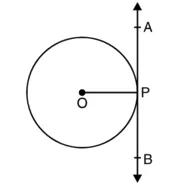
सिद्ध करना है : स्पर्श बिंदु से स्पर्श रेखा पर खींचा गया लंब वृत्त के केंद्र से होकर जाता है।
रचना : OP को मिलाइए।
उपपत्ति : क्योंकि OP वृत्त की त्रिज्या है और AB वृत्त पर स्पर्श रेखा है जिसमें बिंदु P स्पर्श बिंदु है।
∴ ∠OPA = ∠OPB = 90°
[∵ वृत्त के किसी बिंदु पर स्पर्श रेखा, स्पर्श बिंदु से जाने वाली त्रिज्या पर लंब होती है।
या OP ⊥ AB
क्योंकि किसी वृत्त की त्रिज्या सदैव वृत्त के केंद्र से गुजरती है। अतः, स्पर्श
बिंदु से स्पर्श रेखा पर खींचा गया लंब वृत्त के केंद्र से होकर जाता है।

हल :एक वृत्त जिसका केंद्र ‘O’ है। वृत्त के बाहर इसके केंद्र से 5 cm की दूरी पर कोई बिंदु A है।

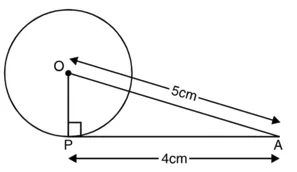
स्पर्श रेखा की लंबाई = PA

= 4 cm

क्योंकि OP त्रिज्या है और PA वृत्त पर स्पर्श रेखा है।

∴ ∠OPA = 90°

अब, समकोण ∆OPA में,

पाइथागोरस प्रमेय का प्रयोग करने पर,

OA² = OP² + PA²
(5 cm)² = OP² + (4 cm)²
या OP² = 25 cm² – 16 cm²
या OP² = 9 cm = (3 cm)²
या OP = 3 cm
अतः, वृत्त की त्रिज्या की लंबाई 3 cm है। उत्तर

हल : दो संकेंद्रीय वृत्त जिनका एक ही केंद्र O तथा त्रिज्याएँ क्रमश: 5 cm और 3 cm हैं।
मान लीजिए PQ बड़े वृत्त की जीवा है परंतु छोटे वृत्त की स्पर्श रेखा है।

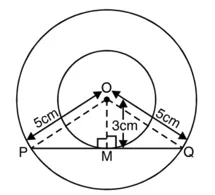
क्योंकि, OM छोटे वृत्त की त्रिज्या है और PMQ स्पर्श रेखा है।
∴ ∠OMP = ∠OMQ = 90°

समकोण त्रिभुजें OMP और OMQ लीजिए।
∠OMP = ∠OMQ = 90°
OP = OQ [एक ही वृत्त की त्रिज्याएँ] OM = OM [उभयनिष्ठ भुजा]

∴ ∆OMP ≅ OMQ [RHS सर्वांगसमता] ∴ PM = MQ [CPCT] या PQ = 2 PM = 2 MQ
अब समकोण, ∆ OMQ में,

पाइथागोरस प्रमेय से,

OQ² = OM² + MQ²
(5 cm)² = (3 cm)² + (MQ)²
या MQ² = 25 cm² – 9 cm²
या MQ² = 16 cm = (4 cm)²
या MQ = 4 cm
∴ जीवा PQ की लंबाई = 2 MQ
= 2 (4) cm
= 8 cm
अतः, अभीष्ट जीवा की लंबाई 8 cm है। उत्तर

हल : दिया है :वृत्त के परिगत एक चतुर्भुज ABCD खींचा गया है। वृत्त का केंद्र O है।

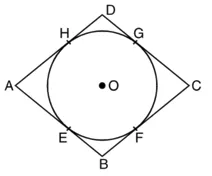
सिद्ध करना है : AB + CD = AD + BC

उपपत्ति : क्योंकि किसी बाह्य बिंदु से वृत्त पर खींची गई स्पर्श रेखाओं की लंबाई बराबर होती है।
अब, B वृत्त के बाहर स्थित कोई बिंदु है और BE; BF वृत्त पर स्पर्श रेखाएँ हैं।
∴ BE = BF …(1)
इसी प्रकार, AE = AH …(2)
और CG = CF …(3)
साथ ही, DG = DH …(4)

(1), (2), (3) और (4) को जोड़ने पर, हमें प्राप्त होता है

(BE + AE) + (CG + DG) = (BF + CF) + (AH + DH)
AB + CD = BC + AD

अभीष्ट परिणाम है।

हल : दिया है : XY तथा X’Y’ केंद्र O वाले वृत्त पर दो समांतर स्पर्श रेखाएँ हैं और स्पर्श बिंदु C पर एक अन्य स्पर्श रेखा AB, XY को A तथा X’Y’ को B पर प्रतिच्छेद करती है।

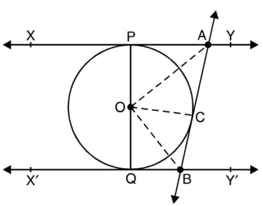
सिद्ध करना है : ∠AOB = 90°

रचना : OC, OA और OB को मिलाइए
उपपत्ति : क्योंकि बाह्य बिंदु से किसी वृत्त पर खींची गई दोनों स्पर्श रेखाओं की लंबाइयाँ समान होती हैं।

अब, A वृत्त के बाहर कोई बिंदु है जिसमें से दो स्पर्श रेखाएँ PA और PC वृत्त पर खींची गई हैं।
∴ PA = PC
साथ ही, ∆ POA और ∆ AOC में,
PA = PC (प्रमाणित)
OA = OA (उभयनिष्ठ भुजा)
OP = OC (एक ही वृत्त की त्रिज्याएँ)

∴ ∆POA ≅ ∆AOC [SSS सर्वांगसमता]

और ∠PAO = ∠CAO [CPCT] या ∠PAC = 2∠PAO = 2∠CAO ….(1)
इसी प्रकार ∠OBC = 2∠OBC = 2 ∠OBQ …(2)
अब, ∠PAC + ∠QBC = 180°

[तिर्यक रेखा AB के एक ही ओर बने अंत: कोणों का योग = 180°]

या 2 ∠CAO + 2∠OBC = 180°
[(1) और (2) का प्रयोग करने पर]

या ….(3)

अब, ∆OAB में,
∠CAO + ∠OBC + ∠AOB = 180°
90° + ∠AOB = 180°
[(3) का प्रयोग करने पर] या ∠AOB = 180° – 90° = 90°
अतः, ∠AOB = 90°

हल : दिया है : एक वृत्त जिसका केंद्र O है। वृत्त के बाहर स्थित किसी बिंदु P से PQ और PR दिए गए वृत्त पर स्पर्श रेखाएँ हैं।

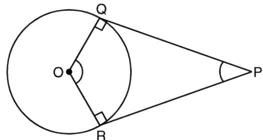
सिद्ध करना है : ∠ROQ + ∠OPR = 180°
उपपत्ति : OQ त्रिज्या है और PQ बिंदु P से दिए गए वृत्त पर स्पर्श रेखा हैं।
∴ ∠OOP = 90° ….(1)

[∵ वृत्त के किसी बिंदु पर स्पर्श रेखा स्पर्श बिंदु से जाने वाली त्रिज्या पर लंब होती है।]

इसी प्रकार ∠ORP = 90° ….(2)
अब, चतुर्भुज ROOP में,
∠ROQ + ∠PRO + ∠OOP + ∠QPR = 360°
या ∠ROQ + 90° + 90° + ∠QPR = 360°

[(1) और (2) का प्रयोग करने पर]

या ∠ROQ + ∠OPR + 180° = 360°
या ∠ROQ + ∠QPR = 360° – 180°
या ∠ROQ + ∠OPR = 180°

अतः, किसी बाह्य बिंदु से किसी वृत्त पर खींची गई स्पर्श रेखाओं के बीच का कोण स्पर्श बिंदुओं को मिलाने वाले रेखाखंड द्वारा केंद्र पर अंतरित कोण का संपूरक होता है।

हल : दिया है : एक समांतर चतुर्भुज ABCD केंद्र O वाले वृत्त के परिगत है।

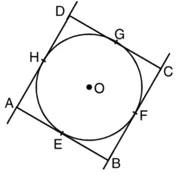
सिद्ध करना है : ABCD एक समचतुर्भुज है।
उपपत्ति : क्योंकि बाह्य बिंदु से किसी वृत्त पर खींची गई दोनों स्पर्श रेखाओं की लंबाइयाँ समान होती हैं।
अब, वृत्त के बाहर स्थित किसी बिंदु B से BE और BF वृत्त पर दो स्पर्श रेखाएँ हैं।
∴ BE = BF …(1)
इसी प्रकार AE = AH …(2)
और CG = CF …(3)
साथ ही, DG = DH …(4)

(1), (2), (3) और (4) को जोड़ने पर हमें प्राप्त होता है

(BE + AE) + (CG + DG)
= (BF + CF) + (AH + DH)
या AB + CD = BC + AD …(5)
अब, ABCD एक समांतर चतुर्भुज है।
∴ AB = CD और BC = AD …(6)

(5) और (6) से हमें प्राप्त होता है।

AB + AB = BC + BC
या 2AB = 2BC
या AB = BC
अब, AB = BC = CD = AD

∴ ABCD समचतुर्भुज है।

अतः किसी वृत्त के परिगत समांतर चतुर्भुज समचतुर्भुज होता है।

हल :4 cm त्रिज्या वाले एक वृत्त के परिगत एक त्रिभुज ABC खींचा गया है। त्रिभुज की भुजाएं BC, CA, AB वृत्त को क्रमशः बिंदुओं D, E तथा F पर स्पर्श करती हैं। क्योंकि किसी बाह्य बिंदु से वृत्त पर खींची गई स्पर्श रेखाओं की लंबाइयाँ बराबर होती हैं।

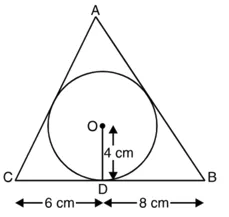
AE = AF = x cm (माना)
CE = CD = 6 cm
और BF = BD = 8 cm

क्योंकि वृत्त की स्पर्श रेखा स्पर्श बिंदु से जाने वाली त्रिज्या पर लंब होती है।

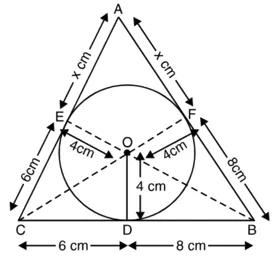
∴ OD ⊥ AB; OE ⊥ AC और OF ⊥ AB.

साथ ही, OE = OD = OF = 4 cm.

∆ ABC लीजिए

α = AC = (???? + 6) cm ;
b = CB = (6 + 8) cm = 14 cm
c = BA = (8 + ????) cm

∴

(∆ABC) का क्षेत्रफल

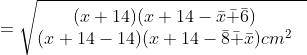
….(1)

(∆OBC) का क्षेत्रफल x आधार x शीर्षलंब

(∆BOA) का क्षेत्रफल x आधार x शीर्षलंब

= (16 + 2????) cm² …(3)

(∆AOC) का क्षेत्रफल x आधार x शीर्षलंब

= (12 + 2????) cm² …(4)

आकृति से, क्षेत्रफलों को जोड़ने से हमें प्राप्त है :

या क्षे० (∆ABC) = क्षे० (∆OBC) + क्षे० (∆BOA) + क्षे० (∆AOC)

√48????² + 672???? = 28 + 16 + 2???? + 12 + 2????
या √48????² + 672???? = 4???? + 56
या √48????² + 672???? = 4[???? + 14]

दोनों ओर वर्ग करने पर हमें प्राप्त होता है –

या 48????² + 672???? = 16 (???? + 14)²
या 48???? (???? + 14) = 16 (???? + 14)²
या 3???? = ???? + 14
या 2???? = 14
या
∴ AC = (???? + 6) cm
= (7 + 6) cm = 13 cm
और AC = (???? + 8) cm
= (7 + 8) cm = 15 cm
अतः, AB = 15 cm और AC = 13 cm उत्तर

हल : दिया है :केंद्र O वाले वृत्त के परिगत बनी चतुर्भुज PORS जिसकी भुजाएँ

PO, QR, RS और SP वृत्त को क्रमश: L, M, N, T पर स्पर्श करती हैं।

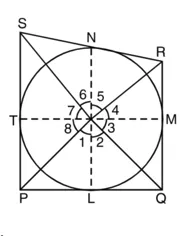
सिद्ध करना है :

∠POQ + ∠SOR = 180°
और ∠SOP + ∠ROQ = 180°

रचना :

OP, OL, OQ, OM, OR, ON, OS, OT को मिलाइए।

उपपत्ति : क्योंकि बाह्य बिंदु से किसी वृत्त पर खींची गई दो स्पर्श रेखाएं केंद्र पर समान कोण अंतरित करती हैं।
∴ ∠2 = ∠3 ; ∠4 = ∠5 ; ∠6 = ∠7 ; ∠8 = ∠1 …(1)

क्योंकि एक बिंदु पर सभी कोणों का जोड़ 360° होता है।

∴ ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 = 360°
या ∠1 + ∠2 + ∠2 + ∠5 + ∠5 + ∠6 + ∠6 + ∠1 = 360°
या 2(∠1 + ∠2 + ∠5 + ∠6) = 360°

या (∠1 + ∠2) + (∠5 + ∠6)

या ∠POQ + ∠SOR = 180°

इसी प्रकार, ∠SOP + ∠ROQ = 180°

अत: वृत्त के परिगत बनी चतुर्भुज की आमने-सामने की भुजाएं केंद्र पर संपूरक कोण अंतरित करती हैं।

इस पोस्ट में आपको Class 10 Maths Chapter 10. वृत्त NCERT Class 10 प्रश्नावली10.1 Mathematics 10. वृत्त Class 10 maths chapter 10 circle solutions Class 10 Maths Chapter 10 Circles Ex 10.2 questions with solutions class 10 maths chapter 10 exercise 10.2 एनसीईआरटी समाधान कक्षा 10 गणित प्रश्नावली 10.2 से संबंधित पूरी जानकारी दी गई है अगर इसके बारे में आपका कोई भी सवाल या सुझाव हो तो नीचे कमेंट करके हम से जरूर पूछें और अगर आपको यह जानकारी फायदेमंद लगे तो अपने दोस्तों के साथ शेयर जरूर करें.