Class 10 Maths Chapter 6 Exercise 6.3 – त्रिभुज

Class 10 Maths Chapter 6 Exercise 6.3 – त्रिभुज

NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.3 – हर विद्यार्थी का सपना होता है कि वे अपनी कक्षा में अच्छे अंक से पास हो ,ताकि उन्हें आगे एडमिशन या किसी नौकरी के लिए फॉर्म अप्लाई करने में कोई दिक्कत न आए . कक्षा 10वीं के विद्यार्थी के लिए यहां पर एनसीईआरटी कक्षा 10 गणित अध्याय 6. (त्रिभुज) प्रश्नावली 6.3 के लिए सलूशन दिया गया है. जोकि एक सरल भाषा में दिया है .ताकि विद्यार्थी को पढने में कोई दिक्कत न आए .इसकी मदद से आप अपनी परीक्षा में अछे अंक प्राप्त कर सकते है.

NCERT Solutions For Class 10th Maths त्रिभुज (प्रश्नावली 6.3)

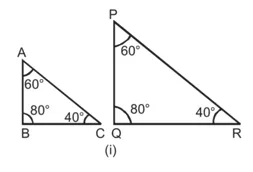
हल : (i) ∆ABC तथा ∆PQR में,
∠A = ∠P (प्रत्येक 60°)
∠B = ∠Q (प्रत्येक 80°)
∠C = ∠R (प्रत्येक 40°)
∴ ∆ABC ~ ∆PQR [AAA समरूपता कसौटी)

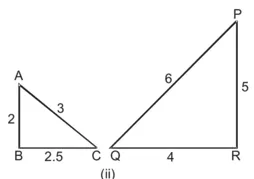
(ii) ∆ABC तथा ∆PQR में,
…(1)
…(2)
…(3)
(1), (2) और (3) से,

∴ ∆ABC ~ ∆QRP [SSS समरूपता कसौटी से]

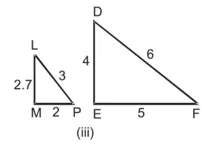
(iii) ∆LMP तथा ∆DEF में,



यहाँ
∴ दो त्रिभुजें समरूप नहीं हैं।
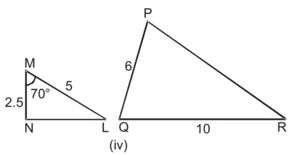
(iv) ∆MNL तथा ∆PQR में,

∠M = ∠Q (प्रत्येक 70°)

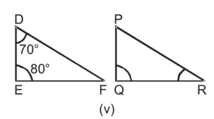
∴ ∆MNL ~ ∆QPR [SAS समरूपता कसौटी से] (v) ∆ABC और ∆DEF में,


∠B ≠ ∠F
∴ ∆ABC तथा ∆DEF समरूप नहीं हैं।
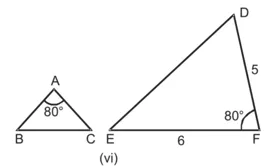
(vi) ∆DEF में,
∠D = 70, ∠E = 80°
∠D + ∠E + ∠F = 180°
70 + 80 + ∠F = 180
∠F = 180 – 70 – 80
∠F = 30°
∆PQR में,
∠Q = 80, ∠R = 30°
∠P + ∠Q + ∠R = 180 (त्रिभुज के कोणों का योगफल)
∠P + 80 + 30 = 180
∠P = 180 -80 -30
∠P = 70°
∆DEF तथा ∆PQR में,
∠D = ∠P (70° प्रत्येक)
∠E = ∠Q (80° प्रत्येक)
∠F = ∠R (30° प्रत्येक)
∴ ∆DEF ~ ∆PQR (AAA समरूपता कसौटी)

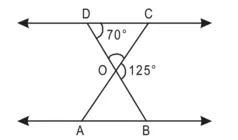
हल : ∠BOC = 125°
∠CDO = 70°
DOC एक सरल रेखा है।
∴ ∠DOC + ∠COB = 180°
∠DOC = 125 = 180
∠DOC = 180 – 125
∠DOC = 55°

∠DOC = ∠AOB = 55° [शीर्षाभिमुख कोण] ∴ ∆ODC – ∆OBA
∠D = ∠B = 70°
∆DOC में, ∠D + ∠O + ∠C = 180°
70° + 55° + ∠C = 180°
∠C = 180 – 70 – 55°
∠C = 55°
∠C = ∠A = 55°
∴ ∠DOC = 55°
∠DOA = 55°
∠OAB = 55°

हल:

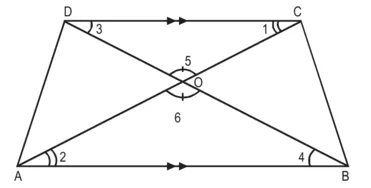
दिया है : समलंब ABCD जिसमें AB || CD है और विकर्ण AC तथा BD परस्पर O पर प्रतिच्छेद करते हैं।
सिद्ध करना है :
उपपत्ति : AB || DC
∆DOC और ∆BOA में,
∠1 = ∠2 (एकांतर कोण)
∠5 = ∠6 (शीर्षाभिमुख कोण)
∠3 = ∠4 (एकांतर कोण)
∴ ∆DOC ~ ∆BOA [AAA समरूपता कसौटी] ∴
[यदि दो त्रिभुजें समरूप हों, तो संगत भुजाएँ समानुपाती होती हैं।
⇒ [अतः सत्यापित]

हल : दिया है ∆TQR

∠1 = ∠2

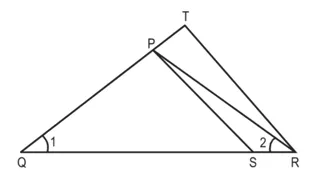
सिद्ध करना है : ∆PQS ~ ∆TQR
उपपत्ति : ∆PQR में,
∠1 = ∠2 (दिया है)
∴ PR = PQ
[समान कोणों की सम्मुख भुजाएँ बराबर होती हैं] (दिया है)

⇒
∆PQS और ∆TQR में,

∠1 = ∠1 (उभयनिष्ठ)
∴ ∆PQS ~ ∆TQR [SAS समरूपता कसौटी] [अतः सत्यापित]

हल : दिया है :- ∆PQR की भुजाओं PR और QR पर क्रमशः बिंदु S और T इस प्रकार स्थित हैं कि ∠P = ∠RTS है।

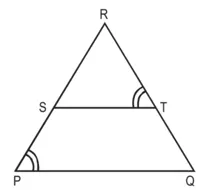
सिद्ध करना है : ∆RPQ ~ ∆RTS
उपपत्ति : ∆RPQ और ∆RTS में,
∠RPQ = ∠RTS (दिया है)
∠R = ∠R [सांझा कोण]∴ ∆PQS ~ ∆RTS [AA समरूपता कसौटी]

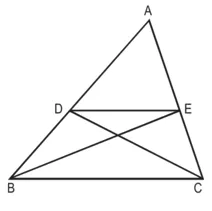
दिया है : ∆ABC और ∆ABE = ∆ACD है।
सिद्ध करना है : ∆ADE ~ ∆ABC
उपपत्ति : ∆ABE = ∆ACD (दिया है)
AB = AC (सर्वांगसम त्रिभुजों के संगत भाग)
और AE = AD
(सर्वांगसम त्रिभुजों के संगत भाग)
…(1)
…(2)
(1) और (2) से,
∆ADE और ∆ABC में,
∠A = ∠A (उभयनिष्ठ)
∴ ∆ADE ~ ∆ABC [SAS समरूपता कसौटी से]

(i) ∆AEP ~ ∆CDP
(ii) ∆ABD ~ ∆CBE
(iii) ∆AEP ~ ∆ADB
(iv) ∆PDC ~ ∆BEC
हल : दिया है : ∆ABC, AD ⊥ BC
CE ⊥ AB,

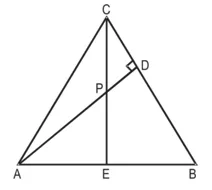
सिद्ध करना है (i) ∆AEP ~ ∆CDP
(ii) ∆ABD ~ ∆CBE
(iii) ∆AEP ~ ∆ADB
(iv) ∆PDC ~ ∆BEC
उपपत्ति : (i) In ∆AEP और ∆CDP में,
∠E = ∠D (प्रत्येक 90°)
∠APE = ∠CPD (शीर्षाभिमुख कोण)
∴ ∆AEP ~ ∆CDP [AA समरूपता कसौटी] (ii) ∆ABD और ∆CBE में,
∠D = ∠E (प्रत्येक 90°)
∠B = ∠B (उभयनिष्ठ)
∴ ∆ABD ~ ∆CBE [AA समरूपता कसौटी] (iii) ∆AEP और ∆ADB में,
∠E = ∠D (प्रत्येक 90°)
∠A = ∠A (उभयनिष्ठ)
∴ ∆AEP ~ ∆ADB [AA समरूपता कसौटी] (vi) ∆PDC और ∆BEC में,
∠C = ∠C (उभनिष्ठ)
∠D = ∠E (प्रत्येक 90°)
∴ ∆PDC ~ ∆BEC [AA समरूपता कसौटी]

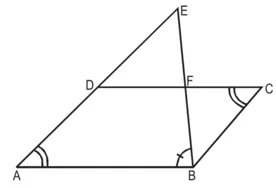
सिद्ध करना है : ∆ABE ~ ∆CFB
उपपत्ति : ∆ABE और ∆CFB में,
∠A = ∠C (|| gm की सम्मुख भुजाएँ)
∠ABE = ∠CFB (एकांतर कोण)
∴ ∆ABE ~ ∆CFB (AA समरूपता कसौटी)

(i) ∆ABC ~ ∆AMP (ii)

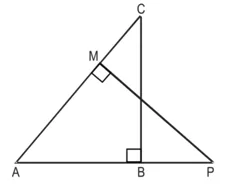
हल : दिया है : ∆ABC और ∆AMP दो समकोण त्रिभुज हैं, जिनके कोण B और M समकोण हैं।
सिद्ध करना है : (i) ∆ABC ~ ∆AMP में
(ii)
उपपत्ति : ∆ABC और ∆AMP में,
∠A = ∠A (उभयनिष्ठ)
∠B = ∠M (प्रत्येक 90°)
∴ ∆ABC ~ ∆AMP (AA समरूपता)
∴
[यदि दो त्रिभुज समरूप हों, तो संगत भुजाएँ समानुपाती होती हैं] [अत: सत्यापित]

(i)
(ii) ∆DCB ~ ∆HGE
(iii) ∆DCA ~ ∆HGF
हल:

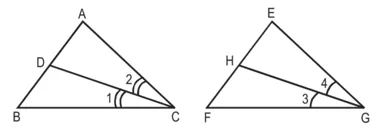
दिया है : ∆ABC और ∆EFG में, CD और GH क्रमश: ∠ACB और ∠EGF के समद्विभाजक हैं अर्थात् ∠1 = ∠2 और ∠3 = ∠4 है।
∆ABC ~ ∆FEG
सिद्ध करना है : (i)
(ii) ∆DCB ~ ∆HGE
(iii) ∆DCA ~ ∆HGE

उपपत्ति : (i) ∆ABC ~ ∆FEG (दिया है)
∠C = ∠G
[यदि दो त्रिभुज समरूप हों, तो संगत कोण बराबर होते हैं।]
∠1 = ∠3 या ∠2 = ∠4
अब, ∆ACD और ∆FGH में,
∠A = ∠F [प्रमाणित ऊपर] ∠2 = ∠4 [प्रमाणित ऊपर]∴ ∆ACD ~ ∆FGH
[∵ AA प्रमाणित समरूपता कसौटी से] Also,

[∵ समरूप त्रिभुजों की संगत भुजाएं समानुपाती होती हैं] (ii) अब, ∆DCB और ∆HGE में,
∠B = ∠E [प्रमाणित ऊपर] ∠1 = ∠3 [प्रमाणित ऊपर] ∴ ∆DCB ~ ∆HGE
[∵ AA समरूपता कसौटी से] (iii) अब, ∆DCA और ∆HGF में,
∠A = ∠F [प्रमाणित ऊपर] ∠2 = ∠4 [प्रमाणित ऊपर] ∴ ∆DCA ~ ∆HGF
[∵ AA समरूपता कसौटी से]

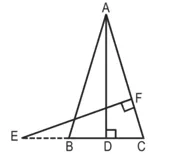
हल : दिया है : AB = AC वाले एक समद्विबाहु ∆ABC की बढ़ाई गई भुजा CB पर स्थित E एक बिंदु है। AD ⊥ BC और EF ⊥ AC है।
सिद्ध करना है : ∆ABD ~ ∆ECF
उपपत्ति : ∆ABC समद्विबाहु त्रिभुज है (दिया है)
AB = AC
(त्रिभुज में समान भुजाओं के सम्मुख कोण बराबर होते है)
∴ ∠B = ∠C (बराबर कोण)
∴ ∆ABD और ∆ECF में,
∠ABD = ∠ECF (ऊपर प्रमाणित)
∠ADB = ∠EFC (प्रत्येक 90°)
∴ ∆ABD ~ ∆ECF [AA समरूपता]

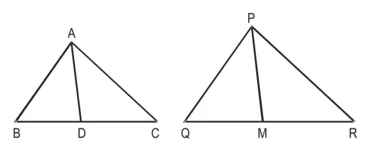
हल : दिया है : ∆ABC और ∆PQR, ∆ABC की भुजाएँ AB, BC और
माध्यिका AD, त्रिभुज PQR की भुजाओं क्रमश: PQ और QR तथा माध्यिका PM के समानुपाती हैं
अर्थात :
सिद्ध करना है : ∆ABC ~ ∆PQR
उपपत्ति : क्योंकि AD और PM माध्यिका है।
⇒ और
अब और
…(1) [दिया है।
⇒
⇒ …(2)
⇒ ∆ADB ~ ∆PMQ [SSS समरूपता कसौटी से] ⇒ ∠ADB = ∠PMQ
[समरूप त्रिभुजों के संगत कोण] ⇒ 180° – ∠ADB
= 180° – ∠PMQ
⇒ ∠ADC = ∠PMR
और [(2) से]

परन्तु [(1) से] ⇒
∴ …(3)
∠ADC = ∠PMR (सिद्ध किया है)
⇒ ∆ADC ~ ∆PMR [SAS समरूपता कसौटी से
⇒
(1) और (4) से
⇒
⇒ ∆ABC ~ ∆PQR [SSS समरूपता कसौटी से]

हल : दिया है : ∆ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि
∠ADC = ∠BAC
सिद्ध करना है : CA² = BC x CD
उपपत्ति : ∆ABC और ∆ADC में,

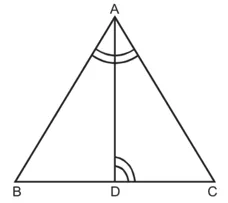
∠C = ∠C (उभयनिष्ठ)
∠BAC = ∠ADC (दिया है)
∴ ∆ABC ~ ∆DAC [AA समरूपता कसौटी से] ∴
[यदि दो त्रिभुज समरूप हों तो संगत भुजाएँ समानुपाती होती हैं।] AC² = BC. DC [अतः सत्यापित]

हल : दिया है : दो त्रिभुज ABC और PQR में D, BC का मध्य-बिंदु है और M, QR का मध्य-बिंदु है।
और …(1)

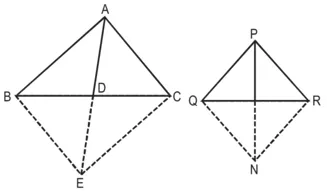
सिद्ध करना है : ∆ABC ~ ∆PQR
रचना : AD को E तक बढ़ाइए ताकि AD = DE हो।
BE और CE को मिलाइए।
PM को N तक बढ़ाइए ताकि PM = MN हो।
QN और NR को मिलाइए।
उपपत्ति : चतुर्भुज ABEC के विकर्ण AE और BC परस्पर D पर समद्विभाजित करते हैं। ∴ चतुर्भुज ABEC एक समांतर चतुर्भुज है।
इसी प्रकार यह दर्शाया जा सकता है कि चतुर्भुज PQNR एक समांतर चतुर्भुज है।
चूँकि ABEC एक समांतर चतुर्भुज है।
∴ BE = AC …..(2)
इसी प्रकार चूँकि DQNR एक || gm है।
∴ QN = PR …..(3)
(2) को (3) से विभाजित करने पर हमें प्राप्त होता है

अब,
∴ ∠BAE = ∠QPN …(5)
(1), (4) और (5) से हमें प्राप्त होता है

अत:, ∆ABE और PQN में से हमें प्राप्त होता है

∴ ∆ABC ~ ∆PQN
∴ ∠BAE = ∠QPN …(6)
इसी प्रकार, यह सिद्ध किया जाता है कि
∆AEC ~ ∆PNR
∴ ∠EAC = ∠NPR …(7)
(6) और (7) को जोड़ने पर हमें प्राप्त होता है।
∠BAE + ∠EAC = ∠QPN + ∠NPR
अर्थात ∠BAC = ∠QPR
अब ∆ABC और ∆PQR में

∠A = ∠P
∴ ∆ABC ~ ∆QPR (SAS समरूपता कसौटी से)

हल :

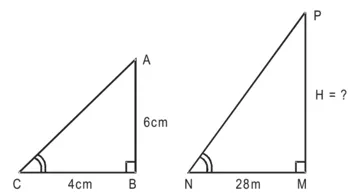
उर्ध्वाधर स्तंभ की लंबाई = 6 m
स्तंभ की छाया की लंबाई = 4 m
मान लीजिए मीनार की ऊँचाई = Hm
मीनार की छाया की लंबाई = 28 m
∆ABC और ∠PMN में,
∠C = ∠N (मीनार की छाया की लंबाई)
∠B = ∠M (प्रत्येक 90°)
∴ ∆ABC ~ ∆PMN [AA समरूपता कसौटी] ∴
[यदि दो त्रिभुजें समरूप हों, तो उनकी संगत भुजाएँ समानुपाती होती हैं।] ∴
H = 6 x 7
H = 42m
∴ मीनार की ऊँचाई = 42 m.

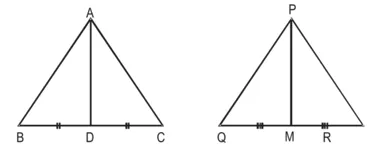
हल : दिया है : ∆ABC और ∆PQR की AD और PM माध्यिकाएँ हैं तथा ∆ABC ~ ∆PQR है।
सिद्ध करना है :
उपपत्ति : ∆ABC ~ ∆PQR (दिया है)

{यदि दो त्रिभुजें समरूप हैं तो उनकी संगत भुजाएँ समानुपाती होती हैं।
∠A = ∠P
{यदि दो त्रिभुजें समरूप हैं, तो उनके संगत कोण बराबर होते हैं।
∠B = ∠Q
∠C = ∠R
D, BC का मध्य बिंदु है।

M, OR का मध्य बिंदु है।

इस पोस्ट में आपको Class 10 Maths Chapter 6 Exercise 6.3 Triangles NCERT solutions class 10 maths chapter 6 exercise 6.3 Class 10 maths chapter 6 exercise 6.3 triangles solutions एनसीईआरटी समाधान कक्षा 10 गणित प्रश्नावली 6.3 कक्षा 10 गणित अध्याय 6 प्रश्नावली 6.3 Class 10th Maths Solution 6.त्रिभुज प्रश्नावली 6.3 से संबंधित पूरी जानकारी दी गई है अगर इसके बारे में आपका कोई भी सवाल या सुझाव हो तो नीचे कमेंट करके हम से जरूर पूछें और अगर आपको यह जानकारी फायदेमंद लगे तो अपने दोस्तों के साथ शेयर जरूर करें.

NCERT Solutions for Class 10 Maths Chapter 6 त्रिभुज Exercise 6.1
NCERT Solutions for Class 10 Maths Chapter 6 त्रिभुज Exercise 6.2
NCERT Solutions for Class 10 Maths Chapter 6 त्रिभुज Exercise 6.3
NCERT Solutions for Class 10 Maths Chapter 6 त्रिभुज Exercise 6.4
NCERT Solutions for Class 10 Maths Chapter 6 त्रिभुज Exercise 6.5
NCERT Solutions for Class 10 Maths Chapter 6 त्रिभुज Exercise 6.6