Class 10 Maths Chapter 3 Exercise 3.6 – दो चर वाले रैखिक समीकरण युग्म

Class 10 Maths Chapter 3 Exercise 3.6 – दो चर वाले रैखिक समीकरण युग्म

10वीं कक्षा के विद्यार्थी के लिए यहां पर एनसीईआरटी कक्षा 10 गणित अध्याय 3. (दो चर वाले रैखिक समीकरण युग्म ) प्रश्नावली 3.6 के लिए सलूशन दिया गया है. जोकि एक सरल भाषा में दिया है .ताकि विद्यार्थी को पढने में कोई दिक्कत न आए .इसकी मदद से आप अपनी परीक्षा में अछे अंक प्राप्त कर सकते है.

Class 10th Maths दो चर वाले रैखिक समीकरण युग्म (प्रश्नावली 3.6)

(i) (ii)

(iii) (iv)

(v) (vi) 6x + 3y = 6xy

2x + 4y = 5xy

(vii)

(viii)

और

और प्रतिस्थापित करने पर

और

या या

या 3u + 2v = 12 …(1) या 2u + 3v = 13 …(2)

(1) को 2 से और (2) को 3 से, गुणा करने पर हमें प्राप्त होता है:

6u + 4v = 24 ….(3)

और 6u + 9v = 39 ….(4)

अब, (4) – (3) से प्राप्त होता है,

6u + 9v = 39

6u + 4v = 24

– – –

5v = 15

या

v के इस मान को (1) में प्रतिस्थापित करने पर, हमें प्राप्त होता है :

3u + 2 (3) = 12

या 3u + 6 = 12

या 3u = 12 – 6 = 6

या

परंतु और

या या

∴ या

अंत:, और

और

और प्रतिस्थापित करने पर

2u + 3v = 2 ….(1)

और 4u – 9v = – 1 ….(2)

(1) को 2 से गुणा करने पर हमें प्राप्त होता है।

4u + 6v = 4 ….(3)

अब, (2) – (3) से प्राप्त होता है :

4u – 9v = – 1

4u + 6v = 4

– – –

– 15v = – 5

v के इस मान को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :

या 2u + 1 = 2

या 2u = 2 – 1 = 1

या

परंतु और

या 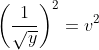या

या या

या

या x = 4 या

या y = 9

अतः, x = 4 और y = 9

और

रखने पर

4v + 3y = 14 …(1)

और 3v – 4y = 23 ….(2)

(1) को 3 से और (2) को 4 से गुणा करने पर हमें प्राप्त होता है :

12v + 9y = 42 …(3)

और 12v – 16y = 92 …(4)

अब, (4) – (3) से प्राप्त होता है :

12v – 16y = 92

12y + 9y = 42

– – –

– 25y = 50

y के इस मान को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :

4v + 3 (-2) = 14

या 4v – 6 = 14

या 4v = 14 + 6 = 20

या

परंतु

या

अतः, और y = – 2 उत्तर

और

और रखने पर

प्राप्त समीकरण है :

5u + v = 2 ….(1)

और 60 – 3y = 1 ….(2)

(1) को 3 से गुणा करने पर हमें प्राप्त होता है :

15u + 3v = 6 ….(3)

अब, (3) + (2) से प्राप्त होता है

15u + 3v = 6

6u – 3y = 1

21u = 7

u के इस मान को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :

या

या

परंतु और

या या

या ???? – 1 = 3 या y – 2 = 3

या ???? = 3 + 1 या y = 3 + 2

या ???? = 4 या y = 5

अतः, x = 4 और y = 5

और

या या

या या

या या

और रखने पर प्राप्त समीकरण है :

-2u + 7v = 5 …(1)

और 7u + 8v = 15 …(2)

(1) को 7 से और (2) को 2 से गुणा करने पर, हमें प्राप्त होता है :

– 14v + 49u = 35 ….(3)

और 14v + 16u = 30 ….(4)

अब, (3) + (4) से प्राप्त होता है :

– 14y + 49u = 35

14y + 16u = 30

65u = 65

u के इस मान को (1) में प्रतिस्थापित करने पर

– 2 (1) + 7v = 5

या 7v = 5 + 2

या 7v = 7

या

परंतु और

या या

या या

या ???? = 1 या y = 1

अंत:, ???? = 1 और y = 1

6???? + 3y = 6????y और 2???? + 4y = 5????y

या या

या या

या या

या या

और प्रतिस्थापित करने पर हमें प्राप्त होता है :

u + 2v = 2 …..(1)

और 4u + 2v = 5

अब, (2) – (1) से प्राप्त होता है

4u + 2v = 5

u + 2v = 2

– – –

3u = 3

या

u के इस मान को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :

1 + 2v = 2

या 2v = 2 – 1 = 1

या

परन्तु और

या और

अतः, ???? = 1 और y = 2

(vii) दिया गया रैखिक समीकरण युग्म है :

और

और को प्रतिस्थापित करने पर

10u + 2v = 4 या 5u + v = 2 …(1)

15u – 5v = -2 …(2)

(1) को 5 से गुणा करने पर हमें प्राप्त होता है

25u + 5y = 10

अब, (3) + (2) से प्राप्त होता है :

25u + 5v = 10

15u – 5v = – 2

40u = 8

u को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :

या 1, = 1 + v = 2

या v = 1

परन्तु और

या या

या

x + y = 5 …(4) या x – y = 1 …(5)

अब, (4) + (5) से प्राप्त होता है :

???? + y = 5

???? – y = 1

2???? = 6

या

???? के इस मान को (4) में प्रतिस्थापित करने पर हमें प्राप्त होता है :

3 + y = 5

y = 5 – 3 = 2

अतः x = 3 और 1 = 2

(viii) दिया गया रैखिक समीकरण युग्म है :

और

और को रखने पर

और

या 4u + 4v = 3 4u या

या 4u + 4v = 3 …(1) या 4u – 4v = – 1 …(2)

अब, (1) + (2) से प्राप्त होता है

4u + 4v = 3

4u – 4v = – 1

8u = 2

u के इस मान को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :

या 4v = 2

या

परंतु और

या ???? + y = 4 …(3) या 3???? – y = 2

अब, (3) + (4) से प्राप्त होता है :

3???? + y = 4

3???? – y = 2

6???? = 6

???? = 1

???? के इस मान को (3) में प्रतिस्थापित करने पर हमें प्राप्त होता है :

3 (1) + y = 4

या 3 + y = 4

या y = 4 – 3 = 1

अतः, ???? = 1 और y = 1

(i) रीतू नदी की धारा की दिशा में 2 घंटे में 20 किमी और धारा के विरुद्ध 2 घंटे में 4 किमी. नाव चला सकती है। स्थिर जल में इसकी नाव चलाने की चाल और धारा की चाल ज्ञात कीजिए।
(ii) 2 औरतें और 5 आदमी एम्ब्राइडरी का काम 4 दिन में पूरा कर सकते हैं जबकि 3 औरतें और 6 आदमी इसे 3 दिन में पूरा कर सकते हैं। औरत अकेले उस काम को कितने दिन में करेगी और 1 आदमी अकेले उस काम को कितने दिन में करेगा ?
(iii) रूही अपने घर के लिए 300 km यात्रा कुछ रेलगाड़ी से और कुछ बस से करती है। यदि वह 60 किमी यात्रा रेलगाड़ी से और शेष बस द्वारा करे तो उसे 4 घंटे लगते हैं। यदि वह 100 km रेलगाड़ी से और शेष बस से यात्रा करे तो उसे 10 मिनट अधिक समय लगता है। रेलगाड़ी की और बस की पृथक-पृथक चाल ज्ञात कीजिए।

= ???? km/h

और धारा की चाल = y km/h

∴ धारा के विरुद्ध चाल = (???? – y) km/h

और धारा की दिशा में चाल = (???? + y) km/h

रीतू द्वारा धारा की दिशा में 2 घंटे में तय की गई दूरी

= चाल x समय

= (???? + y) x 2 km

पहली शर्त अनुसार,

2 (???? + y) = 20

???? + y = 10 …(1)

रीतू द्वारा धारा के विरुद्ध 2 घंटे में तय की गई दूरी

= चाल x समय

= 2 (???? – y) km

दूसरी शर्त अनुसार,

2(???? – y) = 4

???? – y = 2 …(2)

अब, (1) + (2) से प्राप्त होता है :

???? + y = 10

???? – y = 2

2???? = 12

???? के इस मान को (1) में भरने पर हमें प्राप्त होता है:

6 + y = 10

y = 10 – 6 = 4

अतः, रीतू की स्थिर जल में चाल = 6 km/h

और धारा की चाल = 4 km/h

= ???? दिन में

एक आदमी काम को समाप्त कर सकता है = y दिन में

तब, एक औरत का 1 दिन का काम

एक आदमी का 1 दिन का काम

पहली शर्त अनुसार,

दूसरी शर्त अनुसार

और y रखने पर,

समीकरणे (1) और (2) बन जाती हैं :

और

8u + 20v = 1 …(3) 9u + 18y = 1 …(4)

(3) को 9 से और (4) को 8 से गुणा करने पर हमें प्राप्त होता है।

72u + 180v = 9 ….(5)

और 72u + 144v = 8 ….(6)

तब, (5) – (6) से प्राप्त होता है :

72u + 180v = 9

72u + 144v = 8

– – –

36v = 1

v के इस मान को (4) में प्रतिस्थापित करने पर, हमें प्राप्त होता है :

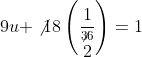
या

या

या

या

परंतु और

या या

या ???? = 18 या y = 36

अतः, एक औरत और एक आदमी अकेले-अकेले काम को क्रमशः 18 दिन और 36 दिन में पूरा कर सकते हैं।

और बस की चाल = y km/h

कुल दूरी = 300 km

स्थिति I

60 किमी दूरी तय करने में लिया गया समय

= दूरी/चाल

= 60/x घंटे

बस द्वारा 240 किमी दूरी तय करने में लिया गया

समय (= 300 – 60)

= 240/y घंटे

∴ कुल समय घंटे

पहली शर्त अनुसार

या ….(1)

स्थिति ॥

रेलगाड़ी द्वारा 100 किमी दूरी तय करने में लगा समय

घंटे

बस द्वारा 200 km दूरी तय करने में लिया गया

समय घंटे

∴ कुल समय घंटे

दूसरी शर्त अनुसार

घंटे 10 मिनट

या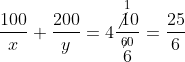

या

और को समीकरणों

(1) और (2) में रखने पर प्राप्त समीकरण हैं :

15u + 60v = 1

और 24u + 48v = 1

या

15u + 60v – 1 = 0

24u + 48v – 1 = 0

या

I और III से हमें प्राप्त होता है :

II और III से हमें प्राप्त होता है :

परंतु और

या या

अतः, रेलगाड़ी की और बस की चाल क्रमश: 60 km/h और 80 km/h है।

इस पोस्ट में आपको Class 10 Maths Chapter 3 Exercise 3.6 Class 10 Maths Chapter 3 Ex 3.6 Pair of Linear Equations in Two Variables class 10 maths chapter 3 exercise 3.2 solutions class 10 maths chapter 3 notes class 10 maths chapter 3 exercise 3.6 solutions pair of linear equations in two variables class 10 solutions एनसीईआरटी समाधान कक्षा 10 गणित अध्याय 3 प्रश्नावली 3.6 दो चर वाले रैखिक समीकरण युग्म कक्षा 10 गणित अध्याय 3 प्रश्नावली 3.6 से संबंधित पूरी जानकारी दी गई है अगर इसके बारे में आपका कोई भी सवाल या सुझाव हो तो नीचे कमेंट करके हम से जरूर पूछें और अगर आपको यह जानकारी फायदेमंद लगे तो अपने दोस्तों के साथ शेयर जरूर करें.

Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.1
Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.2
Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.3
Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.4
Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.5
Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.6
Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.7