Class 10 Maths Chapter 3 Exercise 3.2 – दो चर वाले रैखिक समीकरण युग्म
जो विद्यार्थी 10वीं कक्षा में पढ़ रहे है उनके लिए यहां पर एनसीईआरटी कक्षा 10 गणित अध्याय 3. (दो चर वाले रैखिक समीकरण युग्म ) प्रश्नावली 3.2 के लिए सलूशन दिया गया है. जोकि एक सरल भाषा में दिया है .ताकि विद्यार्थी को पढने में कोई दिक्कत न आए .इसकी मदद से आप अपनी परीक्षा में अछे अंक प्राप्त कर सकते है. इसलिए निचे आपको एनसीईआरटी समाधान कक्षा 10 गणित अध्याय 3 दो चर वाले रैखिक समीकरण युग्म प्रश्नावली 3.2 दिया गया है .
Class 10th Maths दो चर वाले रैखिक समीकरण युग्म (प्रश्नावली 3.2)
(i) कक्षा X के 10 विद्यार्थियों ने गणित की पहेली प्रतियोगिता में भाग लिया। यदि लड़कियों की संख्या लड़कों की संख्या 4 से अधिक हो, तो प्रतियोगिता में भाग लेने वाले लड़के और लड़कियों की संख्या ज्ञात कीजिए।
(ii) 5 पेंसिलों और 7 कलमों का मूल्य ₹ 50 है, जबकि 7 पेंसिलों और 5 कलमों का मूल्य ₹ 46 है। एक पेंसिल और एक कलम का मूल्य ज्ञात कीजिए।
प्रतियोगिता में लड़कों की संख्या = ????
और प्रतियोगिता में लड़कियों की संख्या = y
प्रतियोगिता में भाग लेने वाले कुल विद्यार्थी = 10
∴ ???? + y = 10
या ???? + y – 10 = 0
प्रश्न अनुसार,
y = ???? + 4
या ???? = y – 4
अब रैखिक समीकरणों
???? + y = 10
और ???? – y + 4 = 0 का आलेख खींचिए।
???? + y = 10
या ???? = 10 – y …(1)
y = 0 को (1) में प्रतिस्थापित करनेपर हमें प्राप्त होता है।
???? = 10 – 0 = 10
y = 7 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है
???? = 10 – 7 = 3
y = 10 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है
???? = 10 – 10 = 0
सारणी
| ???? | 10 | 3 | 0 |
| y | 0 | 7 | 10 |
| (????, y) | (10, 0) | (3, 7) | (0, 10) |
बिंदुओं A (10, 0), B (3, 7), C (0, 10) को आलेखित करने और उनको मिलाते हुए रेखा खींचने पर हमें समीकरण ???? + y = 10 का आलेख प्राप्त होता है।
???? – y + 4 = 0
या ???? = y – 4 …(2)
y = 0 को (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है।
???? = 0 – 4 = – 4
y = 7 को (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है।
???? = 7 – 4 = 3
y = 4 को (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है।
???? = 4 – 4 = 0
सारणी
| ???? | -4 | 3 | 0 |
| y | 0 | 7 | 4 |
| (????, y) | (-4, 0) | (3, 7) | (0, 4) |
बिंदुओं D (- 4, 0), B (3, 7), E (0, 4) को आलेखित करने और उनको मिलाते हुए रेखा खींचने पर हमें समीकरण ???? – y + 4 = 0 का आलेख प्राप्त होता है।
आलेख से यह स्पष्ट है कि दोनों रैखिक समीकरण बिंदु B (3, 7) पर मिलते
∴ बिंदु B (3, 7) आलेखीय स्थिति है।
अतः प्रतियोगिता में लड़कों की संख्या = 3
प्रतियोगिता में लड़कियों की संख्या = 7
(ii) मान लीजिए 1 पेंसिल का मूल्य = ₹ ????
और 1 कलम का मूल्य = ₹ y
पहली शर्त अनुसार,
5???? + 7y = 50
दूसरी शर्त अनुसार,
7???? + 5y = 46
∴ रैखिक समीकरण युग्म है :
5???? + 7y = 50
7???? + 5y = 46
अब इन रैखिक समीकरणों का आलेख खींचिए :
5???? + 7y = 50
या 5???? = 50 – 7y
या ![]() ….(1)
….(1)
y = 0 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है।
![]()
x = 10
y = 5 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है।
![]()
![]()
y = 7 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है।
![]()
![]()
सारणी
| ???? | 10 | 3 | 0.2 |
| y | 0 | 5 | 7 |
| (????, y) | (10, 0) | (3, 5) | (0.2, 7) |
बिंदुओं A (10, 0), B (3, 5), C (0.2, 7) को आलेखित करने और उनको मिलाते हुए रेखा खीचने पर हमें समीकरण 5???? + 7y = 50 का आलेख प्राप्त होता है।
7???? + 5y = 46
या 7???? = 46 – 5y
या ![]() …(2)
…(2)
y = 0 को (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है।![]()
= 6.5
y = 5 को (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है।
![]()
y = – 4 को (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है।
![]()
सारणी
| ???? | 6.5 | 3 | 9.5 |
| y | 0 | 5 | -4 |
| (????, y) | (6.5, 0) | (3, 5) | (9.5, -4) |
बिंदुओं E (6.5, 0), B (3, 5), F (9.5, – 4) को आलेखित करने और उनको मिलाते हुए रेखा खीचने पर हमें समीकरण 7???? + 5y = 46 का आलेख प्राप्त होता है। आलेख से यह स्पष्ट है कि दोनों रैखिक समीकरण बिंदु B (3, 5) पर मिलते हैं .:. ∴ बिंदु B (3, 5) आलेखीय स्थिति है।
(i) 5x – 4y + 8 = 0
7x + 6y – 9 = 0
(ii) 9x + 3y + 12 = 0
18x + 6y + 24 = 0
(iii) 6x – 3y + 10 = 0
2x – y + 9 = 0
5???? – 4y + 8 = 0
और 7???? + 6y – 9 = 0
यहाँ α1 = 5, b1 = – 4, c1 = 8
α2 = 7, b2 = 6, c2 = – 9
अब, ![]()
![]()
अतः, दी गई रैखिक समीकरण युग्म एक बिंदु पर प्रतिच्छेद करती हैं।
(ii) दी गई रैखिक समीकरण युग्म हैं :9???? + 3y + 12 = 0
और 18???? + 6y + 24 = 0
यहाँ α1 = 9, b1 = 3, c1 = 12
α2 = 18,b2 = 6, c2 = 24
अब ![]()
![]()
![]()
अतः, दी गई समीकरण-युग्म संपाती हैं।
(iii) दी गई रैखिक समीकरण-युग्म है :6???? – 3y + 10 = 0
और 2???? – y + 9 = 0
यहाँ α1 = 6, b1 = – 3, c1 = 10
α2 = 2, b2 = – 1, c2 = 9
अब, ![]()
![]()
अतः, दी गई रैखिक समीकरण-युग्म एक दूसरे समांतर है।
(i) 3x + 2y = 5; 2x – 3y = 7
(ii) 2x – 3y = 8; 4x – 6y = 9
(iii) ![]()
(iv) 5x – 3y = 11; – 10x + 6y = – 22
(v) ![]() x+2y = 8; 2x + 3y = 12
x+2y = 8; 2x + 3y = 12
3???? + 2y = 5और 2???? – 3y = 7
या 3???? + 2y – 5 = 0
और 2???? – 3y – 7 = 0
यहाँ α1 = 3, b1 = 2, c1 = – 5
α2 = 2, b2 = – 3, c2 = – 7
अब ![]()
∴ ![]()
अतः दी गई रैखिक समीकरण-युग्म संगत है।
(ii) दी गई रैखिक समीकरण-युग्म है :2???? – 3y = 8
और 4???? – 6y = 9
या 2???? – 3y – 8 = 0
4???? – 6y – 9 = 0
यहाँ α1 = 2, b1, = – 3, c1 = – 8
α2 = 4, b2 = – 6, c2 = – 9
अब ![]()
![]()
∴ ![]()
अतः, दी गई रैखिक समीकरण-युग्म असंगत है
(iii) दी गई रैखिक समीकरण-युग्म है :![]()
और 9???? – 10y = 14
या ![]()
और 9???? – 10y – 14 = 0
यहाँ ![]()
α2 = 9, b2 = – 10, c2 = – 14
अब 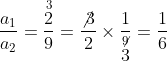
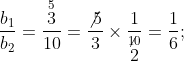
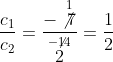
∴ ![]()
अतः, दी गई रैखिक समीकरण-युग्म असंगत है।
(iv) दी गई रैखिक समीकरण-युग्म है :5???? – 3y = 11
और – 10???? + 6y = – 22
या 5???? – 3y – 11 = 0
और – 10???? + 6y + 22 = 0
यहाँ α1 = 5, b1 = – 3, c1 = – 11
α2 = – 10, b2 = 6, c2 = 22
![]()
![]()
∵ ![]()
अतः, दी गई रैखिक समीकरण-युग्म संगत है
(v) दी गई रैखिक समीकरण-युग्म है :![]() ???? + 2y = 8 और 2???? + 3y = 12
???? + 2y = 8 और 2???? + 3y = 12
और ![]() ???? + 2y – 8 = 0
???? + 2y – 8 = 0
या 2???? + 3y – 12 = 0
यहाँ ![]()
α2 = 2, b2 = 3,c2 = – 12
अब 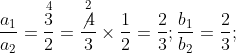
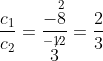
∴ ![]()
अतः, दी गई रैखिक समीकरण-युग्म संगत है।
(i) x + y = 5, 2x + 2y = 10
(ii) x – y = 8, 3x – 3y = 16
(iii) 2x + y – 6 = 0, 4x – 2y – 4 = 0
(iv) 2x – 2y – 2 = 0, 4x – 4y – 5 = 0
x + y = 5
और 2x + 2y = 10
या x + y – 5 = 0
2x + 2y – 10 = 0
यहाँ α2 = 1, b2 = 1, c2 = – 5
α2 = 2, b2 = 2, c2 =
![]()
∴ ![]()
दी गई रैखिक समीकरण युग्म संगत है।
∴ दी गई रैखिक समीकरण युग्म का आलेख खींचिए
???? + y = 5
???? = 5 – y ….(1)
???? = 0 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है
???? = 5 – 0 = 5
???? = 3 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है
???? = 5 – 3 = 2
y = 5 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है।
???? = 5 – 5 = 0
सारणी
| ???? | 5 | 2 | 0 |
| y | 0 | 3 | 5 |
| (????, y) | (5, 0) | (2, 3) | (0, 5) |
बिंदुओंA (5, 0), B (2, 3), C (0, 5) को आलेखित करने और उनको मिलाते हुए रेखा खींचने पर हमें समीकरण ???? + 1 = 5 का आलेख प्राप्त होता है।
2???? + 2y = 10 या 2 (???? + y) = 10
या ???? + y = 5
या ???? = 5 – y …(2)
y = 0 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
???? = 5 – 0 = 5
y = 2 को (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
???? = 5 – 2 = 3
y = 5 को (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
???? = 5 – 5 = 0
सारणी
| ???? | 5 | 3 | 0 |
| y | 0 | 2 | 5 |
| (????, y) | (5, 0) | (3, 2) | (0, 5) |
बिंदुओंA (5, 0), D (3, 2), C (0, 5) को आलेखित करने और उनको मिलाते हुए रेखा खींचने पर हमें समीकरण 2???? + 2y = 10 का आलेख प्राप्त होता है।
आलेख से यह स्पष्ट है कि दी गई रैखिक समीकरण युग्म संपाती रेखाएँ हैं या इनके अपरिमित रूप से अनेकों हल हैं।
(ii) दी गई रैखिक समीकरण-युग्म है :x – y = 8
और 3x – 3y = 16
या x – y – 8 = 0
और 3x – 3y – 16 = 0
यहाँ α1 = 1,b1 = – 1,c1= – 8
α2 = 3,b2 = – 3,c2= – 16
अब ![]()
![]()
∴ ![]()
अतः, दी गई रैखिक समीकरण-युग्म असंगत है।
2???? + y – 6 = 0
और 4???? – 2y – 4 = 0
यहाँ α1 = 2, b1 = 1, c1 = – 6
α2 = 4, b2 = – 2, c2 = – 4
अब, ![]()
![]()
∴ ![]()
∴ दी गई रैखिक समीकरण-युग्म संगत है।
इन रैखिक समीकरणों का आलेख खींचिए
2???? + y – 6 = 0
या 2???? = 6 – y
या ![]() ….(1)
….(1)
y = 0 को (1) में प्रतिस्थापित करने पर, हमें प्राप्त होता है :
![]()
y = 2 को (1), में प्रतिस्थापित करने पर, हमें प्राप्त होता है :
![]()
y = – 2 को (1) में प्रतिस्थापित करने पर, हमें प्राप्त होता है
![]()
![]()
सारणी
| ???? | 3 | 2 | 4 |
| y | 0 | 2 | -2 |
| (????, y) | (3, 0) | (2, 2) | (4, – 2) |
बिंदुओं A (3, 0), B (2, 2), C (4, – 2) को आलेखित करने और उनको मिलाते हुए रेखा खींचने पर हमें समीकरण 2???? + y – 6 = 0 का आलेख प्राप्त होता है।
4???? – 2y – 4 = 0
या 2[2???? – y – 2] = 0
या 2???? – y – 2 = 0
या 2???? = y + 2
या ![]() …(2)
…(2)
y = 0 को (2) में प्रतिस्थापित करने पर, हमें प्राप्त होता है
![]()
y = 2 को (2) में प्रतिस्थापित करने पर, हमें प्राप्त होता है
![]()
y = – 2 को (2) में प्रतिस्थापित करने पर, हमें प्राप्त होता है
![]()
सारणी
| ???? | 1 | 2 | 0 |
| y | 0 | 2 | -2 |
| (????, y) | (1, 0) | (2, 2) | (0, – 2) |
बिंदुओं D (1, 0), B (2, 2), E (0, – 2) को आलेखित करने और उनको मिलाते हुए रेखा खींचने पर हमें समीकरण 4???? – 2y – 4 = 0 का आलेख प्राप्त होता है।
आलेख से यह स्पष्ट है कि दी गई समीकरण-युग्म बिंदु B (2, 2) पर मिलती है।
अतः, दी गई रैखिक समीकरण-युग्म अद्वितीय है।
(iv) दी गई रैखिक किरण-युग्म है2???? – 2y – 2 = 0
और 4???? – 4y – 5 = 0
यहाँ α1 = 2, b1 = – 2, c1 = – 2
α2 = 4, b2 = – 4, c2 = – 5
अब ![]()
![]()
∴ ![]()
अतः, दी गई समीकरण युग्म असंगत है।
हल : मान लीजिए बाग की लंबाई = ???? m
बाग की चौड़ाई = y m
बाग का परिमाप = 2 [???? + y] m
बाग के परिमाण का आधा = (???? + y) m
प्रश्न की पहली शर्त अनुसार,
???? = y + 4
प्रश्न की दूसरी शर्त का अनुसार,
???? + y = 36
∴ रैखिक समीकरण-युग्म है :
???? = y + 4
और ???? + y = 36
???? = y + 4 …(1)
y = 0 को (1) में प्रतिस्थापित करनेपर हमें प्राप्त होता है :
???? = 0 + 4 = 4
y = – 4 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
???? = – 4 + 4 = 0 y
y = 16 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
x = 16 + 4 = 20
सारणी
| ???? | 4 | 0 | 20 |
| y | 0 | -4 | 16 |
| (????, y) | (4, 0) | (0, -4) | (20, 16) |
बिंदुओं A (4, 0), B (0, – 4), C (20, 16) को आलेखित करने और उनको मिलाते हुए रेखा खींचने पर हमें समीकरण ???? = y + 4 का आलेख प्राप्त होता है।
???? + y = 36
???? = 36 – y
y = 12 को (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
???? = 36 – 12 = 24
y = 24 को (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
???? = 36 – 24 = 12
y= 16 को (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
???? = 36 – 16 = 20
सारणी
| ???? | 24 | 12 | 20 |
| y | 12 | 24 | 16 |
| (????, y) | (24, 12) | (12, 24) | (20, 16) |
बिंदुओं D (24, 12), E (12, 24), C (20, 16) को आलेखित करने और उनको मिलाते हुए रेखा खींचने पर हमें समीकरण ???? + y = 36 का आलेख प्राप्त होता है।
आलेख से यह स्पष्ट है कि रैखिक समीकरणों का युग्म बिंदु C (20, 16) पर मिलता है।
∴ C (20, 16) अर्थात् ???? = 20 और y = 16 रैखिक समीकरण युग्म का हल है।
अतः,
बाग की लंबाई = 20 m
बाग की चौड़ाई = 16 m
एक अन्य विधि
मान लीजिए बाग बाग की चौड़ाई = ???? m
बाग की लंबाई = (???? + 4) m
बाग का परिमाप = 2 [लंबाई + चौड़ाई
= 2 [???? + ???? + 4] m
= [2???? + 4] m
∴ बाग के परिमाप का आधा
= (2∴ + 4) m
प्रश्न अनुसार,
2???? + 4 = 36
या 2???? = 36 – 4
या 2???? = 32
या ![]()
अतः, बाग की चौड़ाई = 16 m
और बाग की लंबाई = (16 + 4) m
= 20 m
(i) प्रतिच्छेदित रेखाएँ हों
(ii) समांतर रेखाएँ हों
(iii) संपाती रेखाएँ हों
2???? + 3y – 8 = 0 …(1)
यहाँ पर प्रतिच्छेदित रेखाएं की शर्तों को पूरा करने के लिए अनेक मान है
अर्थात ![]()
इनमें से एक है :
3???? – 2y – 6 = 0 …(2)
अब रैखिक समीकरण (1) और (2) का आलेख खींचिए।
2???? + 3y – 8 = 0
2???? = 8 – 3y
या ![]() …(1)
…(1)
y = 0 को (1) में प्रतिस्थापित करनेपर हमें प्राप्त होता है :![]()
y = – 2 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :![]()
y= 2 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :![]()
सारणी
| ???? | 4 | 7 | 1 |
| y | 12 | 24 | 2 |
| (????, y) | (4, 0) | (7, -2) | (1, 2) |
बिंदुओं A (4, 0), B (7, – 2), C (1, 2) को आलेखित करने और उनको मिलाने पर प्राप्त रेखा खींचने पर हमें समीकरण 2???? + 3y, – 8 = 0 का आलेख प्राप्त होता है।
3???? – 2y – 6 = 0
या 3???? = 6 + 2y
या ![]() ….(2)
….(2)
y = 0 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
![]()
को y = – 3 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
![]()
![]()
y = 3 को (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
![]()
![]()
सारणी
| ???? | 2 | 0 | 4 |
| y | 0 | -3 | 3 |
| (????, y) | (2, 0) | (0, – 3) | (4, 3) |
बिंदुओं D (2, 0), E (0, -3), F (4, 3) को आलेखित करने और उनको मिलाने पर प्राप्त रेखा खींचने पर हमें समीकरण 3???? – 2y – 6 = 0 का आलेख प्राप्त होता है। आलेख से यह स्पष्ट है कि रैखिक किरण युग्म बिंदु G पर प्रतिच्छेद करता है।
स्थिति II. समांतर रेखाएँ दी गई रैखिक किए समीकरण है :
2???? + 3y – 8 = 0 …(1)
यहाँ दो चरों वाली और भी अधिक रैखिक समीकरण हो सकते हैं जो
समांतर रेखाओं की शर्त के संतुष्ट करते हैं अर्थात् ![]()
उनमें से एक है :
2???? + 3y – 5 = 0 …(3)
अब रैखिक समीकरण (1)और (3) का आलेख खींचिए। रैखिक समीकरण 2???? + 3y – 8 = 0 के लिए आलेख है:
सारणी
| ???? | 4 | 7 | 1 |
| y | 0 | -2 | 2 |
| (????, y) | (4, 0) | (7, – 2) | (1, 2) |
2???? + 3y – 5 = 0
या 2???? = 5 – 3y
या ![]() …(3)
…(3)
y = 0 को (3) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
![]()
y = 3 को (3) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
![]()
y = – 3 को (3) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
![]()
सारणी
| ???? | 2.5 | -2 | 7 |
| y | 0 | 3 | -3 |
| (????, y) | (2,5 0) | (-2, 3) | (7, -3) |
बिंदुओं G (2.5, 0), H (- 2, 3), I (7, – 3) को आलेखित करने और उनको मिलाकर रेखा खींचने से हमें समीकरण 2x + 3y – 5 = 0 का आलेख प्राप्त होता है। स्थिति III. संपाती रेखाओं के लिए दी गई रैखिक समीकरण है
2???? + 3y – 8 = 0 …(1)
दो चरों में ऐसे और भी अधिकतम अन्य रैखिक समीकरण हो सकते हैं जो संपाती रेखाओं की शर्त को संतुष्ट करते हों अर्थात्
![]()
अतः उनमें से एक इस प्रकार है :
6???? + 9y – 24 = 0 …(4)
अब रैखिक समीकरणों (1) और (4) का आलेख खींचिए। रैखिक समीकरण (4) लीजिए
6???? + 9y – 24 = 0
या 3 [2???? + 3y – 8] = 0
या 2???? + 3y – 8 = 0
∴ दोनों में बिंदु एक समान है और दोनों समीकरणों की एक ही रेखा है।
???? – y + 1 = 0
और 3???? + 2y – 12 = 0
???? – y + 1 = 0
या ???? = y – 1 …(1)
y = 0 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
???? = 0 – 1 = – 1
y = 3 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
???? = 3 – 1 = 2
y = 1 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
???? = 1 – 1 = 0
सारणी
| ???? | -1 | 2 | 0 |
| y | 0 | 3 | 1 |
| (????, y) | (-1, 0) | (2, 3) | (0, 1) |
बिंदुओं A (-1,0), B (2, 3), C (0, 1) को आलेखित करने और उनको मिला कर रेखा खींचने पर हमें समीकरण x – + 1 = 0 का आलेख प्राप्त होता है।
3???? + 2y – 12 = 0
या 3???? = 12 – 2y
या ![]() …(2)
…(2)
y = 0 को (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
![]()
y = 3 को (2), में प्रतिस्थापित करने पर हमें प्राप्त होता है :
![]()
y = 6 को (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
![]()
सारणी
| ???? | 4 | 2 | 0 |
| y | 0 | 3 | 6 |
| (????, y) | (4, 0) | (2, 3) | (0, 6) |
बिंदुओं D (4, 0), B (2, 3), E (0, 6) को आलेखित करने और उनको मिलाकर रेखा खींचने पर हमें समीकरण 3???? + 2y – 12 = 0
आलेख प्राप्त होता है। रैखिक समीकरणों के युग्म और x-अक्ष द्वारा बनाए गए त्रिभुज के शीर्षों को आलेख में छायांकित किया गया है।
∆ABD इस प्रकार बनी त्रिभुज है।
∆ABD के शीर्षों के निर्देशांक हैं : A (- 1, 0), B (2, 3) और D (4, 0)
अब, आधार AD की लंबाई = AO + OD
= 1 + 4 = 5 मात्रक
लंब BF की लंबाई = 3 units
∴ ∆ABD का क्षेत्रफल = ![]() x आधार x लंब
x आधार x लंब
![]() वर्ग मात्रक
वर्ग मात्रक
![]() वर्ग मात्रक
वर्ग मात्रक
इस पोस्ट में आपको Class 10 Maths Chapter 3 Exercise 3.2 Class 10 Maths Chapter 3 Ex 3.2 Pair of Linear Equations in Two Variables class 10 maths chapter 3 exercise 3.2 solutions class 10 maths chapter 3 notes class 10 maths chapter 3 exercise 3.3 solutions pair of linear equations in two variables class 10 solutions Class 10 maths chapter 3 exercise 3.2 Linear equations in Two Variables एनसीईआरटी समाधान कक्षा 10 गणित अध्याय 3 प्रश्नावली 3.2 दो चर वाले रैखिक समीकरण युग्म कक्षा 10 गणित अध्याय 3 प्रश्नावली 3.2 से संबंधित पूरी जानकारी दी गई है अगर इसके बारे में आपका कोई भी सवाल या सुझाव हो तो नीचे कमेंट करके हम से जरूर पूछें और अगर आपको यह जानकारी फायदेमंद लगे तो अपने दोस्तों के साथ शेयर जरूर करें.
Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.1
Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.2
Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.3
Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.4
Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.5
Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.6
Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.7